Момент первого порядка есть среднее значение (математическое ожидание) случайной величины (2.5). Момент второго порядка
(2.9)
есть средний квадрат случайной величины.
Часто используется так называемое среднеквадратичное значение случайной величины, представляющее собой корень квадратный из среднего квадрата случайной величины:
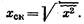(2.10)
Иногда рассматривается центрированное значение случайной величины x0=х-х~, где х~ — среднее значение. Тогда аналогично формуле (2.6) можно ввести понятие центрального момента m- го порядка
(2.11)
Из формулы (2.7) следует, что центральный момент первого порядка всегда равен нулю.
Обратимся теперь к характеристикам рассеяния дискретной случайной величины.
Если х — случайная величина, а х~ — среднее значение этой величины, то величина х-х~ есть отклонение случайной величины от ее среднего значения. Это отклонение является случайной величиной, как и сама величина х.
Средним отклонением А называется среднее значение (математическое ожидание) абсолютной величины отклонения, т. е.
(2.12)
Заметим, что без знака абсолютного значениябылобы
Для рассмотренного выше примера бросания игральной кости
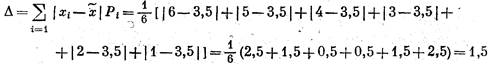
Среднее отклонение случайной величины является уже не случайной величиной, а обычным числом.
Дисперсией называется средний квадрат отклонения случайной величины от ее среднего значения. Она совпадает с центральным моментом второго порядка
(2.13)
Дисперсия может быть легко вычислена на основании свойства среднего значения:
т. е. она равна разности среднего квадрата и квадрата среднего значения случайной величины. Так как всегда выполняется неравенство 
то дисперсия может быть только положительным числом: D ≥ 0.
Корень квадратный из дисперсии называется среднеквадратичным отклонением случайной величины от среднего значения:
(2.14)
Для рассмотренного выше примера бросания игральной кости
Среднеквадратичное отклонение
Укажем простейшие свойства среднеквадратичных отклонений.
1. При сложении независимых случайных величин
дисперсии складываются:
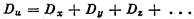
Поэтому среднеквадратичное отклонение суммы независимых случайных величин
Эта формула часто применяется в измерительной технике и в автоматике для вычисления среднеквадратичных ошибок.
2. Пусть имеется п случайных величин
с одинаковыми средними значениями а; и с одинаковыми законами распределения. Тогда их среднее арифметическое
тоже будет случайной величиной с тем же самым средним значением 
но среднеквадратичное отклонение его будет в 
раз меньше, чем для каждой из составляющих (в случае независимых случайных величин):
Например, если производится п измерений одной и той же физической величины, то их среднее арифметическое, хотя тоже является случайной величиной, но всегда надежнее (имеет меньшее среднеквадратичное отклонение), чем каждое измерение в отдельности. Здесь случайные ошибки измерения в известной мере компенсируются. Но надо помнить, что систематические ошибки приборов при этом остаются в полной мере в составе среднего арифметического и никакой массовостью измерений скомпенсированы быть не могут.
3. Для п случайных величин, независимых и имеющих одно и то же среднее значение х~, среднее арифметическое будет при достаточно большом п как угодно мало отличаться от среднего значения х~ (с вероятностью, как угодно близкой к единице). Замечание в скобках означает, что это практически достоверно, но не абсолютно, потому что среднее арифметическое есть все же случайная величина. Таким образом, при большом п и указанных условиях
Этот закон больших чисел, доказанный П. Л. Чебышевым, имеет первостепенное значение для обработки экспериментальных данных и для учетной статистики.
Введем теперь понятие интегрального закона распределения. Интегральным законом распределения или функцией распределения называется вероятность того, что случайная величина примет значение, меньшее некоторого значения х. Математически эта формулировка записывается в виде
где ξ — текущее значение случайной величины х. Например, если график закона распределения дискретной случайной величины х имеет вид, показанный на рис. 2.5, а, то график функции распределения F (х) для нее будет иметь вид, показанный на рис. 2.5, б. Он показывает, что вероятность того, что величина х получит значение меньше единицы, равна нулю; меньше трех — равна 0,2; меньше четырех — равна 0,6 и т. д. Функция распределения F(х) всегда возрастает с увеличением х, причем F(х) =1 при наибольшем возможном значении x max и остается равной единице при всех значениях x > x max
Рис 2.5 а,б,в
Например, для закона Пуассона (3), когда дискретная случайная величина может принимать значения х =0, 1, 2, 3,.... функция распределения
будет иметь вид бесконечной лестницы (см. рис. 2.5, в),ноне заходящей выше единицы, т. е. F(х) → 1 при х→ ∞.