Лекция 7. Основные свойства корреляционных функций случайных процессов

План.

1. Корреляционные функции для типовых сигналов.

2.Аппроксимации корреляционных функции.

3.Связь между видом КФ и видом реализаций процессов.

4.Экспериментальное определение корреляционных функции.

 

Приведем некоторые основные свойства корреляционных функций R_x (t).

1. Начальное значение корреляционной функции равно среднему

значению квадрата случайного процесса:

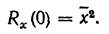(7.1)

Это следует из (6.12), которое при t =0 равно

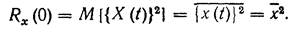(7.2)

2. Конечное значение корреляционной функции равно квадрату среднего значения случайного процесса:

(7.3)

Действительно, чем больше t, тем меньше связаны между собой случайные величины X(t ₁ ) и X(t ₂ ). При t®¥ величины X(t ₁ ) и X(t ₂ ) можно считать взаимно независимыми. Отсюда, принимая во внимание (??) и (6.11), можно написать

(7.4)

 

3. Значение корреляционной функции при любом t не может превышать ее начального значения, т. е.

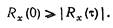(7.5)

Чтобы доказать это, рассмотрим очевидное неравенство

из которого следует

(7.6)

Находим средние значения по времени от обеих частей последнего неравенства:

и

Таким образом, получим неравенство

(7.7)

 

4. Корреляционная функция есть четная функция от t, т. е.

(7.8)

Это вытекает из самого определения корреляционной функции.

Действительно,

(7.9)

Поэтому на графике корреляционная функция всегда симметрична отно­сительно оси ординат.

5. Корреляционная функция суммы случайных процессов Z(t)=X(t)+G(t) определяется выражением

(7.10)

где R_xg (t) и R_gx (t) - взаимные корреляционные функции. Действительно,

(7.11)

6. Корреляционная функция постоянной величины x(t) = А ₀равна квадрату этой постоянной величины A ₀² (рис. 7.1, а), что вытекаетиз самого определения корреляционной функции:

(7.12)

7. Корреляционная функция периодической функции, например x(t) = A sin(w ₁t+ j), представляет собой косинусоиду (рис. 7.1, д), т. е.

(7.13)

имеющую ту же частоту w ₁, что и x(t), и не зависящую от сдвига фазы j.

Чтобы доказать это, заметим, что при нахождении корреляционных функций периодических функций x(t) можно использовать следующее равенство:

(7.14)

где T ₀=2 p / w ₀ — период функции х (t)

Последнее равенство получается после замены интеграла с пределами от -Т до Т при Т ® ¥ суммой отдельных интегралов с пределами от (k -1) T ₀ до kT ₀, где k=0, ±1, ±2,..., ±п, и использования периодичности подынтегральных функций.

Тогда, учитывая сказанное выше, получим

(7.15)

8. Корреляционная функция временной функции, разлагаемой в ряд Фурье:

(7.16)

имеет на основании изложенного выше следующий вид:

R_x (t)= A ₀²+S(A_k ²/2)cos w_kt

Рис 7.1.

9. Корреляционная функция стационарного случайного процесса, на который наложена периодическая составляющая с частотой w_k, также будет содержать периодическую составляющую той же частоты.

Это обстоятельство можно использовать как один из способов об-наружения «скрытой периодичности» в случайных процессах, которая может не обнаруживаться при первом взгляде на отдельные записи реализации случайного процесса.

Примерный вид корреляционной функции процесса X(t), содержащего в своем составе кроме случайной также и периодическую составляющую, показан на рис. 7.2, где R_x0 (t) обозначена корреляционная функция, соответствующая случайной составляющей.

Чтобы выявить скрытую периодическую составляющую (такая задача возникает, на­пример, при выделении малого полезного сигнала на фоне большой помехи), лучше всего определить корреляционную функцию R_x (t) для больших значений t, когда случайный сигнал уже сравнительно слабо коррелирован и случайная составляющая слабо сказывается на виде корреляционной функции.

Рис 7.2

10. Типичная корреляционная функция стационарного случайного процесса с не равным нулю средним значением, не содержащего скрытых периодичностей, приведена на рис. 7.3.

Рис 7.3

Если среднее значение случайного процесса равно нулю, то его типичная корреляционная функция (совпадающая с центрированной корреляционной функцией) будет иметь вид, представленный на рис. 7.1, б, в. В этом случае ее можно аппроксимировать следующим аналитическим выражением:

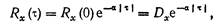(7.17)

где D_x — дисперсия; а =const — параметр затухания.

С ростом t связь между X(t) и X(t+t) ослабевает и корреляционная функция становится меньше. На рис. 7.1, б, в приведены, например, две корреляционные функции и две соответствующие им реализации случайного процесса. Легко заметить, что корреляционная функция, соответствующая случайному процессу с более тонкой структурой, убывает быстрее. Другими словами, чем более высокие частоты присутствуют в случайном процессе, тем быстрее убывает соответствующая ему корреляционная функция.

Иногда встречаются корреляционные функции, которые могут быть аппроксимированы аналитическим выражением

(7.18)

где D_x, — дисперсия; а=const — параметр затухания; g=const — резонансная частота.

Корреляционные функции подобного вида имеют, например, случайные процессы типа турбулентности атмосферы, фединга радиолокационного сигнала, углового мерцания цели и т. п.

Выражения (7.17) и (7.18) часто используются для аппроксимации корреляционных функций, полученных в результате обработки экспериментальных данных.

11. Чем слабее взаимосвязь между предыдущими X(t) и последующими X(t + ) значениями случайного процесса, тем быстрее убывает корреляционная функция R_x (t).

Время t_R, при котором имеет место неравенство | R_x (t_R)-(х)²|<=D, где D — достаточно малая величина, называют временем корреляции случайного процесса.

Случайный процесс, в котором отсутствует связь между предыдущими и последующими значениями, называют чистым случайным процессом или белым шумом. В случае белого шума время корреляции t_R =0 и корреляционная функция представляет собой d-функцию (см. рис. 7.1, г):

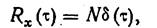(7.19)

где N =const.

Заметим, что случайный процесс типа белого шума является физически нереальным, так как ему соответствуют бесконечно большое значение дисперсии и среднего значения квадрата случайной величины D_x = х ² =R_х (0)=oо, а следовательно, и бесконечно большая мощность.

При решении практических задач часто пользуются нормированной корреляционной функцией

(7.20)

Нормированная корреляционная функция удобна тем, что всегда r_x (0) = 1. Иногда в рассмотрение вводят нормированную взаимную корреляционную функцию

(7.21)

причем можно показать, что

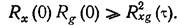(7.22)

В заключение кратко рассмотрим способ экспериментального определения корреляционных функций.

Если имеется экспериментальная запись реализации x(t) случайного процесса X(t) на достаточно длительном интервале времени, то корреляционная функция R_x (t), определяемая выражением (7.18), может быть приближенно вычислена следующим образом. Весь интервал записи осциллограммы делится на l равных частей, длительность которых Dt=T/l выбирается такой, чтобы реализация x(t) мало изменялась на протяжении интервала Dt (рис. 7.4).

Рис 7.4

Значение ординаты реализации x(t) на некотором отрезке п обозначим x_n, а значение ординаты этой же кривой, но смещенной на величину t=mDt, т. е. x(t + t), обозначим х_п+т.

Задаваясь различными значениями т, находим для различных значений t=mDt среднее значение произведения ординат х_п и х_п+т. Приближенное значение корреляционной функции

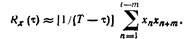(7.23)

В (54) уменьшение интервала Т на величину t обусловлено тем, что ординаты х_п+т, известны только до t=Т-t =(l-т)Dt. Чем меньше длительность отрезков Dt и чем больше величина интервала Т, тем точнее выражение (7.23) соответствует корреляционной функции R_x (t). Для получения ошибки не более 2% должно выполняться неравенство т <=0,1 T / Dt.

Приведенный способ определения корреляционной функции по экспериментально полученной реализации случайного процесса довольно трудоемок, поэтому на практике обычно корреляционные функции находят при помощи специальных приборов — корреляторов, которые автоматически вычисляют средние произведения двух ординат осциллограмм, находящихся друг от друга на расстоянии т.

Если экспериментально найденная корреляционная функция R_x () содержит постоянную составляющую x, то, используя (6.13), можно найти центрированную корреляционную функцию т. е.