Спектральная плотность ошибки

(11.13)

По известной спектральной плотности S_e (w) определяют затем составляющую среднего значения квадрата ошибки e_f².

Аналогично определяют остальные составляющие среднего значения квад­рата ошибки.

 

 

Определение средней квадратической ошибки при случайных и ре­гулярных воздействиях, действующих одновременно.

 

Внешние воз­действия G(t) или F(t) могут представлять собой произвольно изменяю­щиеся во времени регулярные сигналы, на которые наложены стацио­нарные случайные процессы. В таких случаях при расчете систем ав­томатического управления внешние воздействия удобно представить следующим образом:

(11.14)

где т_g(t), m_f(t) — эквивалентные регулярные составляющие внешних воздействий, включающие в себя как математическое ожидание соот­ветствующего случайного процесса, так и регулярный внешний сигнал;

— центрированные случайные составляющие полезного сигнала и помехи соответственно.

Любую искомую координату системы можно представить в виде двух составляющих: регулярной составляющей (математического ожидания) и центрированной случайной составляющей. Например, ошибку системы E(t) можно записать в виде

(11.15)

Таким образом, нахождение случайной ошибки Е(t) может быть сведено к нахождению ее математического ожидания т_e(t) (регулярной составляющей ошибки) и центрированной случайной составляющей Е⁰(t). При этом в линейной системе на основании принципа суперпози­ции т_e(t) и E⁰(t) складываются из составляющих от действия полез­ного сигнала и помехи, которые можно находить порознь.

Математическое ожидание т_(t) можно рассматривать как реакцию линейной системы на регулярные внешние воздействия т_g(t) и m_f(t) и определять через передаточные функции системы:

(11.16)

где W_ge(p)= 1/[1+ W(р) ] — передаточная функциязамкнутой сис­темы, связывающая ошибку и управляющийсигнал; W_f(p) = W₂(p)/ [1+ W(р) ] — передаточная функция замкнутой системы, связывающая ошибку и помеху [см. (???)].

Установившееся значение (математическое ожидание) ошибки m_e(t) при медленно меняющихся регулярных функциях т_g(t) и m_f(t) обычно определяют методом коэффициентов ошибок.

В частном случае, если регулярные внешние воздействия постоян­ны (либо отсутствуют), а случайные воздействия представляют собой стационарные случайные процессы, то т_g = const и m_f = const. В этом случае ошибка E(t) будет являться стационарным случайным процессом, математическое ожидание которого т_e определяется через уравнение статики системы:

(11.17)

Центрированные случайные составляющие любой координаты сис­темы, например центрированную случайную составляющую ошибки системы Е⁰(t), можно рассматривать как реакцию системы на центрированные случайные составляющие управляющего сигнала G⁰(t) и помехи F⁰(t). Поскольку Е⁰(t) представляет собой случайный процесс, то находят не мгновенные значения E⁰(t), а некоторые ее статистические характеристики: дисперсию, среднее квадратическое отклонение и др.

Центрированные случайные составляющие внешних воздействий G⁰(t) и F⁰(t) могут быть заданы либо центрированными корреляци­онными функциями R_g^o (t), R_f^o(t и R_g⁰_f0(t), либо центрированными спектральными плотностями S_g⁰(w), S_f⁰(w) и S_g0_f0(jw), зная которые можно определить либо центрированную корреляционную функцию ошибки R_e0(t), либо центрированную спектральную плотность ошибки.

Обычно проще находить центрированную спектральную плотность ошибки, которая в соответствии с (??) имеет вид

(11.18)

где S_g0_f0(jw), S_f0_g0(jw) — взаимные спектральные плотности между G⁰(t) и F⁰(t).

При отсутствии корреляции между полезным сигналом и помехой их взаимные спектральные плотности равны нулю и центрированная спектральная плотность ошибки

(11.19)

В соответствии с (7??) дисперсия ошибки

(11.20)

Нахождение дисперсии связано с вычислением интеграла (11.20), который определяют аналогично интегралу (??). Среднее значение квадрата ошибки

(11.21)

где т_e(t) — математическое ожидание ошибки, определяемое по (11.17), a D_e — дисперсия ошибки — по (11.20).

Зная e², можно вычислить среднюю квадратическую ошибку:

(11.22)

Заметим, что если математическое ожидание ошибки, определяе­мое по (11.16), постоянно, то

(11.23)

и в этом случае среднее значение квадратаошибки, определяемое по формуле (11.23), полностью совпадает со средним значением квадрата ошибки, вычисляемым по (??).

В частном случае, когда внешние воздействия не содержат регуляр­ных составляющих, а представляют собой центрированные стационар­ные случайные процессы, т_e =0 и критерием динамической точности системы можно считать дисперсию ошибки

(11.24)

или среднее квадратическое отклонение

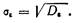(11.25)

 

Пример 1.

На входе замкнутой следящей системы с единичной обратной связью (рис. 11.1) действуют случайный полезный сигнал G(t), имеющий спект­ральную плотность , и случайная помеха F(t) типа «белый шум», спектральная плотность которой S_f(w)=N. Корреляция между полезным сигналом и помехой отсутствует.

Передаточная функция разомкнутой следящей системы W(р)=К/р (1 + рТ). Определить среднюю квадратическую ошибку системы при D_g= 100 В; Т_g= 20с; N =0,01 В²/Гц; Т =0,1 с; К= 5 1/с.

1. Находим передаточные функции замкнутой системы по ошибке и регулируе­мой величине:

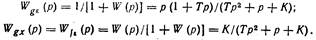
2. Спектральная плотность ошибки и соответствии с (???)

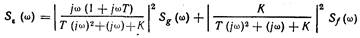
3. Находим составляющую среднего квадрата ошибки, обусловленную полезным сигналом:

Сравнивая полученное выражение с видом подынтегральной функции (???), можно выписать полиномы H(jw) и M(jw), т. е.

следовательно, коэффициенты a_i равны:

Полином M(jw) должен быть записан в виде

Из справочной литературы для п= 3 находим значение табличного интеграла J₃ т. е.

Окончательно получаем

4. Находим составляющую среднего квадрата ошибки, обусловленную помехой

Сравнивая последнее выражение с видом подынтегральнойфункции (???), выписываем полиномы H(jw) и М(jw), т. е.

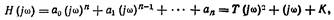
следовательно, коэффициенты а, равны: a₀ = T; a₁=1; a₂ =K. Полином M(jw) должен быть записан в виде

В данном случае n=2, поэтому и, следовательно,

коэффициенты b_i равны: b₀ =0; b₁=1.

Из справочной литературы для п = 2 находим J₂ =(- b₀+a₀b₁/a₂)/(2a₀a₁) =1/2K.

 

Окончательно получаем

5. Находим результирующее значение среднего квадратаошибки:

Подставляя численные значения параметров, получаем

Средняя квадратическая ошибка

 

Пример 2

Решить предыдущую задачу графоаналитическимметодом. 1. Находим выражение для спектральной плотности ошибки:

Подставляя численные значения параметров, получаем

Задавая различные значения  в пределах от 0 до 20, вычисляем S_() и записываем результаты:

2. Строим график S _e (w) (рис. 11.4), разбивая который на типовые фигуры (прямоугольники, треугольники, трапеции) находим величину площади П_e, ограниченной кривой S_e(w) и осью абсцисс:

Рис 11.4

3. Определяем среднее значение квадрата ошибки:

и среднюю квадратическую ошибку:

Следует отметить, что рассмотренная выше задача быстрее и проще решается ана­литическим методом, который к тому же позволяет устано­вить аналитическую связь между величиной средней квадратической ошибки и параметрами системы. При­ближенный графоаналитиче­ский метод интегрирования спектральной плотности целе­сообразно применять лишь при значениях п > 4, когда аналитический метод оказы­вается слишком громоздким.

 

Пример 3.

Решить предыдущую задачу при условии, что на входе сис­темы действует регулярный полезный сигнал g(t)=а+Vt, где а= 10В;

V= 1B/c.

Полезный сигнал смешан со случайной помехой F(t) типа «белый шум», спектральная плотность которой S_f(w) = N.

1. Поскольку полезный сигнал g(t) — регулярная функция времени, то среднее значение квадрата ошибки в соответствии с (???).

где m_(t) = W_g(p) g(t) — динамическая составляющая ошибки, обусловленная регулярным полезным сигналом g(t); e_f²=D_e — среднее значение квадрата слу­чайной составляющей ошибки, обусловленное случайной помехой F(t). Величина e_f² была определена в примере 1, она равна e_f²=KN/2.

2. Определим установившееся значение регулярной составляющей ошибки т(t) методом коэффициентов ошибок:

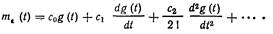
Для нахождения коэффициентов ошибок С_о, С₁, C₂,... разложим передаточ­ную функцию W_ge(р) =1/[1+ W(р) ], связывающую полезный сигнал и помеху, в ряд по возрастающим степеням р, что удобно, например, сделать, разделив числитель выражения для W_ge(p) на его знаменатель:

следовательно. С_о=0; с₁=1/K; c₂/2! = (КТ - 1)/K².

В нашем случае dg(t)/dt=V, а все последующие производные от полезного сигнала равны нулю. Поэтому окончательно получаем

3. Находим результирующее значение среднего квадратаошибки:

Подставляя численные значения коэффициентов, получаем

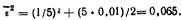
Средняя квадратическая ошибка