План.
1.Постановка задачи расчета стохастической САУ.
2.Критерии точности стохастических САУ.
3.Аналитический метод определения
средней квадратической ошибки (СКО).
4.Графоаналитический метод определения СКО.
5.Определение СКО при случайных и
регулярных воздействиях, действующих одновременно.
6.Примеры расчета стохастических САУ.
7.Сравнительный анализ методов расчета.
Рассмотрим замкнутую линейную следящую систему (рис.11.1), предназначенную для возможно более точного воспроизведения случайного полезного сигнала G(t), действующего на входе системы, при наличии случайной помехи F(t), приложенной в произвольной точке системы.
Внешние воздействия обычно задаются корреляционными функциями Rg (t) и Rf (t) или спектральными плотностями Sg (w) и Sf (w). Если полезный сигнал и помеха коррелированы, то задается также взаимная корреляционная функция Rgf (t) или взаимная спектральная плотность Sgf (jw).
Если внешние воздействия G(t) и F(t) являются стационарными случайными процессами, то в устойчивой линейной системе с постоянными параметрами в установившемся режиме все координаты системы [например, регулируемая величина X(t), ошибка E(t) и т.д.] также будут являться стационарными случайными процессами. В отличие от детермированных систем при расчете систем, подверженных случайным внешним воздействиям, находят не мгновенные значения интересующих нас координат системы, а их статистические (вероятностные) характеристики.
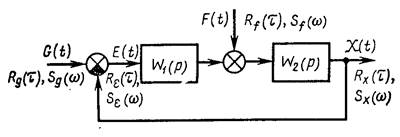
Рис 11.1
При расчете системы сначала по заданным корреляционным функциям или спектральным плотностям внешних воздействий определяют корреляционные функции или спектральные плотности интересующих нас координат системы, а затем, используя их, находят математическое ожидание, дисперсию и другие статистические характеристики этих координат.
Связь между корреляционными функциями входных воздействий Rg (t), Rf (t) и Rgf (t) и корреляционными функциями искомой координаты, например корреляционной функцией Rx (t) регулируемой случайной величины X(t), может быть найдена на основе (10.20) или (10.23). Зная корреляционную функцию Rx (t), можно определить следующие статистические характеристики случайной регулируемой величины:
среднее значение регулируемой величины
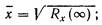
среднее значение квадрата регулируемой величины
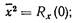
дисперсию регулируемой величины
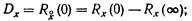
среднее квадратическое отклонение регулируемой величины
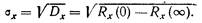
Спектральные плотности искомых координат определяют по заданным спектральным плотностям внешних воздействий Sg (w), Sf (w) и Sgf(jw) на основе (10.20) или (10.24). После того как будет определена, например, спектральная плотность регулируемой величины, среднее значение квадрата регулируемой величины может быть найдено по формуле
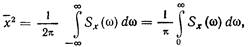(11.1)
которая получается из (??) и (??).
При расчетах систем автоматического управления часто интересуются динамической точностью системы, которая при стационарных случайных воздействиях определяется средним значением квадрата случайной ошибки системы, равной
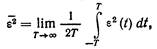(11.2)
где е(/) — любая реализация случайной ошибки; Т — интервал наблюдения.
Среднее значение квадрата случайной ошибки может быть определено через спектральную плотность ошибки по формуле, аналогичной (11.1), т. е.
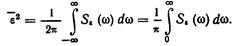(11.3)
Средняя квадратическая ошибка
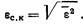
Разумеется, статистические характеристики случайной ошибки можно определять и по корреляционной функции ошибки Rs (-с), используя формулы, аналогичные (??) — (??), однако в практических расчетах чаще всего пользуются формулой (11.3), которая быстрее и проще приводит к цели. Входящую в (11.3) спектральную плотность ошибки для рассматриваемой системы (рис. 11.1) при коррелированных полезном сигнале и помехе в соответствии с (??) вычисляют по формуле
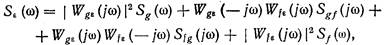(11.4)
где Sg (w), Sf(w) — спектральные плотности полезного сигнала и помехи; Sgf (w, Sfg(w) — взаимные спектральные плотности между полезным сигналом и помехой; Wg(jw) =l/[l+ W(jw)] — частотная передаточная функция, связывающая ошибку e(t) и полезный сигнал g(t); Wfe(jw) = W2(jw)/ [1+ W(jw) ] — частотная передаточная функция, связывающая ошибку e(t) и помеху f(t); W(jw)=W1(jw) W2(jw) — частотная передаточная функция разомкнутой системы; W2(jw)— частотная передаточная функция части разомкнутой системы между точкой приложения помехи и выходом системы.
При отсутствии корреляции между полезным сигналом и помехойих взаимные спектральные плотности равны нулю и выражение для спектральной плотности ошибки упрощается:
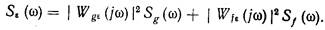(11.5)
Среднее значение квадрата ошибки системы в общем случае состоит из отдельных составляющих, определяемых слагаемыми (11.5), т. е.
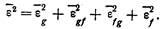(11.6)
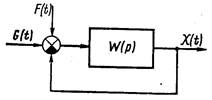
Рис 11.2
В частном случае, когда помеха действует на входе в месте приложения управляющего воздействия (рис. 11.2) и корреляция между полезным сигналом и помехой отсутствует, (11.5) можно записать в виде
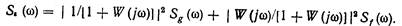(11.7)
Заметим, что (11.3), (11.4) и (11.7) для спектральной плотности ошибки Se(w) могут быть легко переписаны для спектральной плотности регулируемой величины Sx(w), если в них заменить частотную передаточную функцию для ошибки Wge(jw) на частотную передаточную функцию замкнутой системы Wgx(jw).
Чтобы найти среднее значение квадрата ошибки системы при случайных воздействиях, необходимо, зная спектральную плотность ошибки Se(w), вычислить интеграл (11.3). Вычисление этого интеграла довольно сложно, поэтому на практике его выполняют двояко: либо аналитическим методом с помощью табличных интегралов, либо методом графоаналитического интегрирования.