Задача о плотности материальной точки.

Попытаемся определить плотность, создаваемую материальной точкой массы 1.

Положим, что эта точка есть начало координат. Чтобы определить плотность, распределим единичную массу равномерно внутри шара радиуса ε с центром в 0. В результате получим среднюю плотность f_ε(x), равную

Но нас интересует плотность при (т.е. ε стремится к 0 справа). Примем сначала в качестве искомой плотности δ(x) предел последовательности средних плотностей f_ε(x) при , то есть функцию

(3)

От плотности δ естественно требовать, чтобы интеграл от нее по всему пространству давал бы полную массу вещества, то есть

. (4)

Но для функции δ(x), определенной формулой (3), 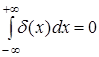. Это значит, что функция не восстанавливает массу (не удовлетворяет требованию (4)) и поэтому не может быть принята в качестве искомой плотности. Таким образом, предел последовательности средних плотностей f_ε(x) не подходит для наших целей, то есть не может быть принят в качестве плотности δ(x).

Для любой непрерывной функции φ(x) найдем слабый предел последовательности при .

Покажем, что

(5)

Действительно, в силу непрерывности функции φ(x) для любого η>0 существует такое ε₀>0, что , коль скоро . Отсюда при всех получаем

Покажем, что .

Так как (здесь dx фактически равен dV), то - объем шара радиуса ε. Следовательно,

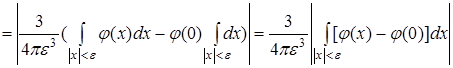Формула (5) обозначает, что слабым пределом последовательности функций f_ε(x), , является функционал φ(0) (а не функция!), сопоставляющий каждой непрерывной функции φ(x) число φ(0) – ее значение в точке x=0. Этот функционал принимается за определение плотности δ(x) – это и есть дельта-функция Дирака. Итак, можно записать

, ,

понимая под этим предельное соотношение (5). Значение функционала δ на функции φ – число φ(0) – обозначается так:

(6)

Это равенство дает точный смысл дельта-функции, введенной Дираком, обладающей следующими свойствами:

δ(x)=0, x≠0, 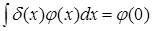, C.

Роль интеграла здесь играет величина - значение функционала δ на функции φ.

Таким образом, дельта-функция - функционал, сопоставляющий по формуле =φ(0) каждой непрерывной функции φ число φ(0)- ее значение в нуле.

Проверим, что функционал δ восстанавливает полную массу. Действительно, роль интеграла играет величина , равная, в силу (6), значению функции, тождественно равной 1, в точке x=0, то есть =1(0)=1.

Таким образом, плотность, соответствующая точечному распределению масс, не может быть описана в рамках классического понятия функции, и для ее описания следует привлекать линейные (непрерывные) функционалы.

1.3. Математическое определение функции Дирака.

Функция δ(x) применяется не только в механике, а во многих разделах математики, в частности при решении многих задач уравнений математической физики.

Пусть f(t) - функция, непрерывная на (a;b), а - иглообразная функция. Для дальнейшего введения определения дельта-функции Дирака рассмотрим поведение интеграла

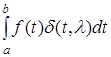при

Рассмотрим (a;b), содержащий внутри себя точку t=0, то есть a<0<b и . Из определения иглообразной функции и обобщенной теоремы о среднемполучаем:

, где .

Если , то и , а в силу непрерывности функции f(t) и . Поэтому при a<0<b

(7)

Если же числа a и b одинаковых знаков (a<b<0 или 0<a<b), то есть (a;b) не содержит внутри себя точки t=0, то

при всех достаточно малых λ.

Если числа a и b имеют одинаковые знаки, то при , если a>0 (рис.6), или при , если b<0 (рис.7), интервал 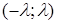не будет пересекаться с (a;b), а поэтому для всех

и .

Следовательно,

(8)

Введём обозначение:

(9)

Таким образом, δ(t) – обобщенная функция, характеризующая предельное поведение иглообразной функции при и использующаяся при вычислении интегралов.

Дельта-функцию можно применять и формально, пользуясь лишь следующим ее основным свойством, вытекающим из равенств (7) - (9) для любой непрерывной функции.

(10)