Неопределённость характеризуется величиной, называемой энтропией (от греческого «эн-тропо» обращение (превращение)).
В физике его ввел Р. Клаузиус в 70-80 г. г. 19-го века. В дальнейшем это понятие широко использовалось в термодинамике.
Энтропия замкнутого пространства определяется через вероятности pi нахождения элементов (например, молекул) в i –той зоне, ячейке:
где 
, К – постоянная Больцмана;
или в информационном виде:
,
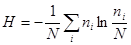где N – общее число элементов (молекул) в пространстве, 
– число элементов (молекул) со скоростями от 
до 
.
Можно записать 
.
Пусть некоторый дискретный источник информации обладает конечным алфавитом из М элементов, обозначаемых x1,x2,…,xM. Каждый элемент имеет свою вероятность появления p1,p2,…,pM. Тогда ансамбль можно задать в виде матрицы:
.
Такой ансамбль А показывает, что некоторая физическая система может находиться в М различных состояниях или в ней может происходить М событий. Иногда это называют конечной схемой.
В большинстве реальных случаях реализация элемента xi зависит от символа xj, который был в предыдущий момент. Тогда можно записать матрицу условных вероятностей:
.
При создании сообщения неопределённость выбора элементов xi удобно характеризовать энтропией источника, которая при независимых элементах с независимой вероятностью равна:
.
Для случая зависимых вероятностей, выражаемых матрицей 
, безусловная энтропия источника может быть получена по формуле:
.
Как связаны понятия энтропии и количество информации.
По Хартли: если n – число равновероятных исходов, то количество информации, полученное при реализации одного из них, равно 
. После опыта ситуация считается полностью определённой, т.е. апостериорная вероятность равна 1.
По Шеннону: количество информации J определяется как разность энтропии до проведения эксперимента Hапр и после проведения эксперимента Hапост. Это случай неравновероятных исходов:
J = Hапр - Hапост.
Для каналов передачи информации (передача символа Х-эксперимент, приём символа Y-результат) среднее количество информации, приходящейся на передачу/приём одного символа, равно
,
где 
– неопределённость ситуации (переданного символа Х) при условии, что символ Y принят.
Для каналов передачи сигналов без потерь Hапост = 0, т.е. принятый символ Y однозначно определяет переданный источником символ Х. При этом
.
Определение количества информации достаточно произвольно. Последняя формула даёт количество информации в битах. Если основание логарифма в ней заменить на 10, то количество информации определяется в дитах, если в формулу подставить натуральный логарифм – в натах. Таким образом, 1 дит - количество информации, получаемое при реализации одного из 10 равновероятных исходов эксперимента.
В общем случае, если взаимозависимость простирается более чем на два элемента, определение среднего количества информации на элемент требует привлечения более сложных условных вероятностей
.
Например, для n = 2
.
Ещё раз: по определению количество информации, переносимой в среднем одним элементом равно энтропии источника.
Пример.
Определим количество информации, передаваемой в секунду в телевизионном изображении с 
элементами, с числом градаций цвета h = 128 и с частотой развёртки m = 25 кадров / сек.
Рассмотрим случай равновероятных состояний любой точки экрана. В этом случае энтропия максимальна
;
.
Оценка апостериорной информации по Хартли:
.
Известно, что пропускная способность глаза 50 – 100 бит/сек, т.е. мозг человека реагирует на ограниченное количество информации – главные моменты, изменения. Используя способность сопоставлять, запоминать, прогнозировать, мозг избавляется от необходимости «снимать» для анализа всю информацию. Вместо этого идёт сопоставление с имеющейся в мозгу моделью процесса или изображения.