Постановка задачи синтеза.

Лекция 14. Синтез линейных систем с минимальной средней квадратической ошибкой.

План.

1.Общая постановка задачи синтеза оптимальной САУ.

2.Классификация задач синтеза.

3.Синтез при заданной структуре системы.

4.Примеры параметрического синтеза оптимальных САУ.

Постановка задачи синтеза.

Рассмотрим систему автоматического управления с передаточной функцией W_з(p), служащую для усиления и преобразования управляющего полезного сигнала G(t) при наличии случайной помехи F(t). Это преобразование в общем случае производит­ся в соответствии с некоторым заданным оператором (алгоритмом преобразования) Н(р) (рис. 14.1).

В общем случае система должна возможно более точно воспроизводить на своем выходе не само упра­вляющее воздействие G(t), а некоторую функцию от управляющего воздействия

(14.1)

Рис. 14.1

В системах, находящихся под воздействием случайного (или регу­лярного) полезного сигнала и случайной помехи, возникает задача отделения полезного сигнала от помехи и подавления (фильтрации) последней. Эту задачу называют задачей фильтрации или сглаживания.

Введение преобразующего оператора Н(р) обобщает задачу не толь­ко на обычные следящие системы, у которых Z(t)=G(t) [т. е. Н(р)=1 ], но и на другие классы систем, выполняющие различные преоб­разования управляющего сигнала. В зависимости от вида оператора Н(р) задача фильтрации сочетается с задачей воспроизведения [если Н(р)=const ], упреждения (предсказания), или экстраполяции [если Н(р)=е^rt ], интегрирования [если Н(р)=1/р ], дифференцирования [если Н(р)=р ] и др. В общем случае преобразующий оператор Н(р) может быть произвольным.

Идеальное преобразование полезного сигнала в соответствии с (???) невозможно из-за динамических ошибок системы, а также из-за наличия возмущающих воздействий (помех). Поэтому выходной сигнал (регулируемая величина) X(t) будет отличаться от воспроиз­водимого сигнала Z(t).

Разность

(14.2)

называют случайной ошибкой системы.

Синтез систем при случайных воздействиях заключается в опре­делении динамических характеристик системы, наилучшим образом обеспечивающих выполнение некоторого статистического критерия оптимальности. Существуют различные статистические критерии оп­тимальности. Однако наиболее часто за статистический критерий оп­тимальности принимают критерий минимума средней квадратической ошибки

(14.3)

где e(t) — любая реализация случайной ошибки.

В этом случае задача синтеза состоит в том, чтобы найти такую фи­зически реализуемую оптимальную передаточную функцию замкнутой системы W_зoпт(p), при которой было бы минимальным среднее значе­ние квадрата ошибки

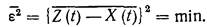
(14.4)

Согласно критерию средней квадратической ошибки, оценка точности системы производится в зависимости от среднего, а не мгновенного значения ошибки, что не всегда является достаточным, например тогда, когда требуется, чтобы ошибка не выходила за заданные пределы. Применение этого критерия может оказаться нерациональным и в тех случаях, когда требования к величине ошибки в разные моменты времени неодинаковы.

Однако, несмотря на то, что этот критерий, впрочем, как и всякий другой косвенный критерий, не является универсальным, он благодаря своей простоте получил широкое практическое применение.

При воздействии на систему не коррелированных между собой стационар­ного случайного сигнала и помехи в соответствии с (???) среднее значение квадрата ошибки состоит из двух составляющих:

(14.5)

Если бы к системе было приложено только одно внешнее воздействие, либо полезный сигнал G(t), либо помеха F(t), то теоретически соответствующим выбором параметров передаточной функции (полосы пропускания) системы можно было бы обеспечить любую точность систем. Однако при одновременном действии полезного сигнала и помехи точность системы не может быть любой.

Это наглядно видно из рис. 14.2, где изображены (полученные ниже в при­мере 5) типичные графики зависимости составляющих ошибки e_g² и e_f² от величины коэффициента усиления разомкнутой системы K. Для лучшего воспро­изведения управляющего сигнала G(t), т. е. уменьшения составляющей ошибки e_g² система должна иметь возможно больший коэффициент усиления. Однако, для того чтобы лучше подавлять помеху F(t), т. е. уменьшить составляющую ошибки e_g² система, наоборот, должна иметь возможно меньший коэффициент K. Поэтому, когда на систему действуют одновременно полезный сигнал и поме­ха, существует некоторое компромиссное (оптимальное) решение и соответствую­щие ему оптимальные параметры системы (в данном случае К_опт), при которых среднее значение квадрата ошибки будет минимальным, меньше которого его, при заданных статистических характеристиках управляющего сигнала и помехи, никаким изменением параметров сделать нельзя.

Рис. 14.2

В зависимости от вида графиков спектральной плотности управляющего сигнала и помехи способы решения задачи синтеза при слу­чайных воздействиях могут быть различны.

В простейшем случае, когда спектры частот полезного сигнала S_g(w) и помехи S_f(w) не налагаются друг на друга (рис. 14.3, а), ам­плитудно-частотную характеристику замкнутой системы A(w) выби­рают достаточно широкой для обеспечения требуемой точности воспро­изведения управляющего сигнала и в то же время достаточно узкой для того, чтобы система меньше реагировала на помеху.

Рис. 14.3

Если управляющий сигнал имеет спектр частот, очень быстро убы­вающий с возрастанием частоты, а спектр помех близок к белому шуму (рис. 14.3, б), то в этом случае форма амплитудно-частотной характерис­тики | W(jw) | разомкнутой системы должна выбираться при низких частотах, где | W(jw) |>>1 и сконцентрирована основная энергия управляющего сигнала, возможно более близкой к форме спектральной плотности управляющего сигнала S_g(w), а затем должна быстро убывать, по возможности следуя за убывающей характеристикой S(w). Наиболее общим является случай, когда спектры частот полезного сигнала и помехи накладываются друг на друга и имеют произволь­ную форму (рис. 14.3, в). В этом случае при синтезе систем со случай­ными воздействиями различают два вида задач:

1. Синтез при заданной структуре системы управления, когда до­биваются минимума средней квадратической ошибки, выбирая опти­мальные параметры корректирующих звеньев системы на основании известных статистических характеристик полезного сигнала и помехи.

2. Синтез при произвольной структуре системы управления, когда по заданным статистическим характеристикам полезного сигнала и помехи определяют оптимальную структуру и параметры системы, при которых обеспечивается минимум средней квадратической ошибки.