Устройство, имеющее способность преобразовывать полученную теплоту в механическую работу носит название теплового двигателя. В таких машинах механическая работа совершается в процессе расширения вещества, называющегося рабочим телом. Его роль обычно исполняют газообразные вещества, вроде паров бензина, воздуха и водяного пара.
Определение 1
Рабочее тело приобретает или отдает тепловую энергию при теплообмене с телами, которые имеют внушительный запас внутренней энергии. Такие тела называют тепловыми резервуарами.
Исходя из первого закона термодинамики, можно сделать вывод, что полученное газом количество теплоты QQ полностью преобразуется в работу AA в условиях изотермического процесса, при котором внутренняя энергия не претерпевает изменений (ΔU=0)(ΔU=0):
A=QA=Q
Однако, подобный однократный акт превращения теплоты в работу для техники не представляет интереса. Существующие тепловые двигатели, такие как паровые машины, двигатели внутреннего сгорания и им подобные, работают циклически. Необходимо периодическое повторение процесса теплопередачи и преобразования полученной теплоты в работу. Чтобы данное условие выполнялось, рабочее тело должно совершать круговой процесс или же термодинамический цикл, при котором исходное состояние с периодически восстанавливается. На рисунке 3.11.13.11.1 в виде диаграммы (p, V)(p, V) газообразного рабочего тела с помощью замкнутых кривых проиллюстрированы круговые. В условиях расширения газ производит положительную работу A1A1, эквивалентную площади под кривой abcabc. При сжатии газ совершает отрицательную работу A2A2, равную по модулю площади под кривой cdacda. Полная работа за цикл A=A1+A2A=A1+A2 на диаграмме (p, V)(p, V) равняется площади цикла. Работа AA положительна, в том случае, если цикл проходит по часовой стрелке, и AA отрицательна, когда цикл проходит в противоположном направлении.

Рисунок 3.11.1.3.11.1. Круговой процесс на диаграмме (p, V)(p, V). abcabc – кривая расширения, cdacda – кривая сжатия. Работа AA в круговом процессе равна площади фигуры abcdabcd.
Все круговые процессы обладают общей чертой. Они не могут привестись в действие при контакте рабочего тела только с одним тепловым. Их минимальное число должно быть равным двум.
Определение 2
Тепловой резервуар, обладающий более высоким значением температуры, носит название нагревателя, а с более низким – холодильника.
Рабочее тело при совершении кругового процесса получает от нагревателя некоторую теплоту Q1>0Q1>0 и теряет, отдавая холодильнику, количество теплоты Q2<0Q2<0. Для полного полученного рабочим телом за цикл количества теплоты Q справедливо следующее выражение:
Q=Q1+Q2=Q1−|Q2|Q=Q1+Q2=Q1-Q2.
Совершая цикл, рабочее тело приходит в свое первоначальное состояние, из чего можно сделать вывод, что изменение его внутренней энергии равняется ΔU=0ΔU=0. Основываясь на первом законе термодинамики, запишем:
ΔU=Q−A=0∆U=Q-A=0.
Из этого следует:
A=Q=Q1−|Q2|A=Q=Q1-Q2.
Работа AA, которую рабочее тело совершает за цикл, эквивалентна полученному за этот же цикл количеству теплоты QQ.
Определение 3
Коэффициентом полезного действия или же КПД ηη теплового двигателя называют отношение работы AA к полученному рабочим телом за цикл от нагревателя количеству теплоты Q1Q1, то есть:
η=AQ1=Q1−|Q2|Q1η=AQ1=Q1-Q2Q1.

Рисунок 3.11.2.3.11.2. Модель термодинамических циклов.
Коэффициент полезного действия теплового двигателя демонстрирует, какая доля тепловой энергии, которую получило рабочее тело от нагревателя, преобразовалась в полезную работу. Оставшаяся часть (1–η)(1–η) была без пользы передана холодильнику. Коэффициент полезного действия тепловой машины не может быть больше единицы η<1η<1. На рисунке 3.11.33.11.3 проиллюстрирована энергетическая схема тепловой машины.
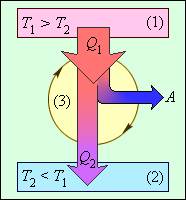
Рисунок 3.11.3.3.11.3. Энергетическая схема тепловой машины: 11 – нагреватель; 22 – холодильник; 33 – рабочее тело, совершающее круговой процесс. Q1>0, A>0, Q2<0; T1>T2Q1>0, A>0, Q2<0; T1>T2.
Виды тепловых двигателей
В технике свое применение находят двигатели, использующие круговые процессы. Рисунок 3.11.33.11.3 демонстрирует нам циклы, применяемые в бензиновом карбюраторном и в дизельном двигателях. Они оба в качестве рабочего тела используют смесь паров бензина или дизельного топлива с воздухом. Цикл карбюраторного двигателя внутреннего сгорания включает в себя две изохоры (1–2, 3–4)(1–2, 3–4) и две адиабаты (2–3, 4–1)(2–3, 4–1), дизельного двигателя -две адиабаты (1–2, 3–4)(1–2, 3–4), одну изобару (2–3)(2–3) и одну изохору (4–1)(4–1). Реальный КПД (коэффициент полезного действия) у карбюраторного двигателя составляет около 30 %30 %, у дизельного двигателя – приблизительно 40 %40 %.

Рисунок 3.11.4.3.11.4. Циклы карбюраторного двигателя внутреннего сгорания (1)(1) и дизельного двигателя (2)(2).
Мы помогаем студентам с дипломными, курсовыми, контрольными Узнать стоимость
Цикл Карно
Круговой процесс, изображенный на рисунке 3.11.53.11.5, состоящий из двух изотерм и двух адиабат был назван циклом Карно в честь открывшего его в 18241824 году французского инженера. Данное явление впоследствии оказало колоссальное влияние на развитие учения о тепловых процессах.

Рисунок 3.11.53.11.5.. Цикл Карно.
Находящийся в цилиндре, под поршнем, газ совершает цикл Карно. На участке изотермы (1–2)(1–2) он приводится в тепловой контакт с нагревателем, обладающим некоторой температурой T1T1. Газ изотермически расширяется, при этом к нему подводится эквивалентное совершенной работе A12A12 количество теплоты Q1=A12Q1=A12. После этого на участке адиабаты (2–3)(2–3) газ помещается в адиабатическую оболочку и продолжает процесс расширения при отсутствующем теплообмене. На данной части цикла газ совершает работу A23>0A23>0. Его температура при адиабатическом расширении снижается до величины T2T2. На идущем следующим участке изотермы (3–4)(3–4) газ приводится в тепловой контакт с холодильником в условиях температуры T2<T1T2<T1. Производится процесс изотермического сжатия. Газом совершается некоторая работа A34<0A34<0 и отдается тепло Q2<0Q2<0, эквивалентное произведенной им работе A34A34. Его внутренняя энергия не претерпевает изменений. На последнем оставшемся участке адиабатического сжатия газ снова помещают в адиабатическую оболочку. При сжатии его температура вырастает до величины T1T1, также совершается работа A41<0A41<0. совершаемая газом за цикл полная работа A эквивалентна сумме работ на отдельных участках:
A=A12+A23+A34+A41A=A12+A23+A34+A41.
На диаграмме (p, V)(p, V) данная работа равняется площади цикла.
Процессы на любом из участков цикла Карно квазистатичны. Например, оба участка 1–21–2 и 3–43–4, относящихся к изотермическим, производятся при пренебрежительно малой разности температур рабочего тела, то есть газа, и теплового резервуара, будь то нагреватель или холодильник.
Исходя из первого закона термодинамики, можно заявить, что работа газа в условиях адиабатического расширения или сжатия эквивалентна падению значения ΔUΔU его внутренней энергии. Для 11 моля газа верно следующее выражение:
A=−ΔU=−CV(T2−T1)A=-∆U=-CV(T2-T1),
в котором T1T1 и T2T2 представляют собой начальную и конечную температуры рабочего тела.
Из этого следует, что работы, совершаемые газом на двух адиабатических участках цикла Карно, противоположны по знакам и одинаковы по модулю:
A23=−A41A23=-A41.
Коэффициент полезного действия ηη цикла Карно может рассчитываться с помощью следующих соотношений:
η=AQ1=A12+A34Q12=Q1−|Q2|Q1=1−|Q2|Q1η=AQ1=A12+A34Q12=Q1-Q2Q1=1-Q2Q1.
С. Карно выразил коэффициент полезного действия цикла через величины температур холодильника T2T2 и нагревателя T1T1:
η=T1−T2T1=1−T2T1η=T1-T2T1=1-T2T1.
Цикл Карно примечателен тем, что ни на одном из его участков тела, обладающие различными температурами, не соприкасаются. Любое состояние рабочего тела в цикле является квазиравновесным, что означает его бесконечную близость к состоянию теплового равновесия с окружающими объектами, то есть тепловыми резервуарами или же термостатами. В цикле Карно исключен теплообмен в условиях конечной разности температур рабочего тела и окружающей среды (термостатов), если тепло имеет возможность переходить без совершения работы. По этой причине любые другие возможные круговые процессы проигрывают ему в эффективности при заданных температурах нагревателя и холодильника:
η Карно =ηmaxηКарно=ηmax

Рисунок 3.11.6.3.11.6. Модель цикла Карно.
Каждый участок цикла Карно и цикл в целом могут проходиться в обоих направлениях.
Определение 4
Обход цикла по часовой стрелке соответствует тепловому двигателю, в котором полученное рабочим телом тепло частично преобразуется в полезную работу. Обход против часовой стрелки соответствует холодильной машине, где некое количество теплоты отходит от холодного резервуара и передается горячему резервуару за счет совершения внешней работы. Именно поэтому идеальное устройство, работающее по циклу Карно, носит название обратимой тепловой машины.
В реально существующих холодильных машинах применяются разные циклические процессы. Любой холодильный цикл на диаграмме (p, V)(p, V) обходятся против часовой стрелки. На рисунке 3.11.73.11.7 проиллюстрирована энергетическая схема холодильной машины.

Рисунок 3.11.7.3.11.7. Энергетическая схема холодильной машины. Q1<0, A>0, Q2 > 0, T1>T2Q1<0, A>0, Q2 > 0, T1>T2.
Работающее по холодильному циклу устройство может обладать двояким предназначением.
Определение 5
Если полезным эффектом является отбор некоторого количества тепла |Q2|Q2 от охлаждаемых тел, к примеру, от продуктов в камере холодильника, то такое устройство является обычным холодильником.
Эффективность работы холодильника может быть охарактеризована следующим отношением:
βx=|Q2||A|βx=Q2A.
Таким образом, эффективность работы холодильника представляет собой количество тепла, отбираемого от охлаждаемых тел на 1 джоуль 1 джоуль затраченной работы. В условиях подобного определения β х βх может быть, как больше, так и меньше единицы. Для обращенного цикла Карно справедливо выражение:
βx=T2T1−T2βx=T2T1-T2.
Определение 6
В случае, когда полезным эффектом является передача некоего количества тепла
|Q1||Q1| нагреваемым телам, чьим примером может выступать воздух в помещении, то такое устройство называется тепловым насосом.
Эффективность β Т βТ теплового насоса может быть определена с помощью отношения:
β т =|Q1||A|βт=Q1A.
То есть она может определяться количеством теплоты, передаваемым более теплым телам на 1 джоуль 1 джоуль затраченной работы. Из первого закона термодинамики следует:
|Q1|>|A|Q1>A.
Следовательно, β Т βТ всегда больше единицы. Для обращенного цикла Карно справедливо следующее выражение:
β т =1η=T1T1−T2βт=1η=T1T1-T2.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter