F = не A
| A | не А |
Логическое отрицание: ИНВЕРСИЯ - если исходное выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное выражение ложно, то результат отрицания будет истинным. Данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО
| A | B | F |
F = A & B.
Логическое умножение КОНЪЮНКЦИЯ - это выражение будет истинным только тогда, когда истинны оба исходных простых выражения. Конъюнкция определяет соединение двух логических выражений с помощью союза И.
| A | B | F |
F = A + B
Логическое сложение – ДИЗЪЮНКЦИЯ - это выражение будет истинным тогда и только тогда, когда истинно хотя бы одно из исходных (простых) выражений. Дизъюнкция определяет соединение двух логических выражений с помощью союза ИЛИ
Логическое следование: ИМПЛИКАЦИЯ - связывает два простых второе (В)– следствием из этого условия. результатом ИМПЛИКАЦИИ является ЛОЖЬ только тогда, когда условие А истинно, а следствие В ложно. Обозначается символом "следовательно" и выражается словами ЕСЛИ …, ТО …
| A | B | F |
| A | B | F |
Логическая равнозначность: ЭКВИВАЛЕНТНОСТЬ - определяет результат сравнения двух простых логических выражений А и В. Результатом ЭКВИВАЛЕНТНОСТИ является новое логическое выражение, которое будет истинным тогда и только тогда, когда оба исходных выражения одновременно истинны или ложны. Обозначается символом "эквивалентности"
Порядок выполнения логических операций в сложном логическом выражении:
1. инверсия
2. конъюнкция
3. дизъюнкция
4. импликация
5. эквивалентность
Для изменения указанного порядка выполнения операций используются скобки.
Основные законы логики: А = А – закон тождества
А & 
= 0 – закон непротиворечия.
(Закон выражает тот факт, что высказывание не может быть одновременно истинным и ложным)
A Ú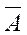 
= 1 – закон исключенного третьего. (Закон означает, что либо высказывание истинно, либо его отрицание должно быть истинным).
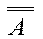= А – закон двойного отрицания
Свойства констант:
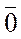= 1 
= 0
А Ú 0 = А А & 0 = 0
А Ú 1 = 1 А & 1 = A
Законы идемпотентности:
А Ú А = А А & А = A
Законы коммутативности:
А Ú В = В Ú А А & В = В & А
Законы ассоциативности:
А Ú (В Ú С) = (АÚ В) Ú С
А & (В & С) = (А & В) & С
Законы дистрибутивности:
А Ú (В & С) = (АÚ В) & (А Ú С)
А & (В Ú С) = (А & В) Ú (А& С)
Законы поглощения:
А Ú (А & В) = А
А & (А Ú В) = А
Законы де Моргана:
В справедливости указанных законов можно убедиться с помощью таблиц истинности
Базовые логические элементы компьютера
Логический элемент И
конъюнктор
Логический элемент ИЛИ
дизъюнктор
Логический элемент НЕ
инвертор
Построение таблиц истинности для сложных выражений:
Количество строк = 2n + две строки для заголовка (n - количество простых высказываний)
Количество столбцов = количество переменных + количество логических операций
При построении таблицы надо учитывать все возможные сочетания логических значений 0 и 1 исходных выражений. Затем – определить порядок действий и составить таблицу с учетом таблиц истинности основных логических операций.
ПРИМЕР: составить таблицу истинности сложного логического выражения
D = не A & (B+C)
А, В, С - три простых высказывания, поэтому:
количество строк = 23 +2 = 10 (n=3, т.к. на входе три элемента А, В, С)
количество столбцов:
1) А
2) В
3) С
4) не A это инверсия А (обозначим Е)
5) B + C это операция дизъюнкции (обозначим F)
6) D = не A & (B+C), т.е. D = E & F это операция конъюнкции
| А | В | С | E = не А (не 1) | F = В+С (2+3) | D = E&F(4*5) |
| o | |||||
| o | |||||