Определение 1.
Функция 
называется бесконечно малой функцией, или бесконечно малой величиной, в точке 
, если
или 
. (1)
ПРИМЕР 1.
– бесконечно малая величина в точках 
и 
.
Замечание!
Понятие «бесконечно малая» величина нельзя смешивать с понятием «очень малая величина», т. к. последняя является константой, а бесконечно малая величина – переменная, промежуточные значения которой могут быть и большими, но ее предел стремится к нулю.
Определение 2.
Определение на языке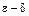 
. Функция 
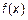– бесконечно малая величина в точке , если 
.
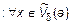
Теорема 1.
Для того чтобы b было пределом функции 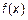в точке 
, необходимо и достаточно, чтобы разность между 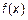и ее пределом в этой точке была бесконечно малой величиной.
Доказательство. Необходимость.
Дано: 
. Необходимо доказать, что 
. Из условия и определения предела следует, что 
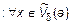
, то есть 
. Следовательно, 
– бесконечно малая величина в точке .
Достаточность. Дано: , где – бесконечно малая величина. Необходимо доказать, что 
. Из того, что – бесконечно малая величина, следует, что 
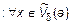
, или 
.
Определение 3.
Второе определение предела. Число b называется пределом функции 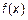в точке , если 
есть бесконечно малая величина .
3. Свойства бесконечно малых величин
3.1. Сумма бесконечно малых величин
Теорема 2.
Алгебраическая сумма конечного числа бесконечно малых величин в точке есть величина бесконечно малая в этой точке, т. е. 
- бесконечно малая величина в точке 
, если 
.
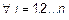Доказательство.
Докажем, что теорема верна для двух слагаемых: 
.
Если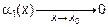 
, то согласно определению 
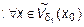
. Если 
, то согласно определению 
. Для любых 
можно принять 
. Для дельта-окрестности 
= 
оценим 
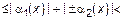
, то есть 
и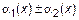 
– бесконечно малая величина. Для суммы n бесконечно малых величин с учетом предыдущего доказательство сводится к последовательному объединению слагаемых до случая суммы двух бесконечно малых величин.
Если число слагаемых 
, то получим неопределенность 
.
3.2. Произведение бесконечно малой величины в точке на функцию
Теорема 3.
Произведение бесконечно малой величины в точке на функцию, ограниченную в окрестности этой точки, есть бесконечно малая величина.
Доказательство.
Пусть 
, то согласно определению 
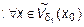
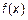. Пусть функция – ограничена в окрестности 
, 
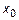. Примем 
= 
, для которой выполняются предыдущие условия. Для любых можно принять 
. Оценим 
. Таким образом, 
, . Следовательно, 
– бесконечно малая величина, т. е. если , а 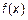имеет в точке 
конечный предел, то 
.
Важно!
Очевидно, что произведение n бесконечно малых величин есть бесконечно малая величина. Если число произведений , то получим неопределенность 
.
Определение 3.
Функция 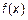бесконечно большая величина в точке , если 
, 
(неограниченная).
или 
. (2)
ПРИМЕР 2. 
.
Важно!
Бесконечно большую величину нельзя путать с очень большой величиной (const). Среди постоянных чисел есть 0, его можно принять за бесконечно малую величину, за бесконечно большую величину ни одно из чисел принять нельзя.
Теорема 4.
Величина, обратная бесконечно малой величине в некоторой точке, есть величина бесконечно большая и наоборот.
Доказательство.
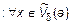
а) По условию , откуда следует 
. Обозначим 
. Следовательно, согласно определению 
есть бесконечно большая величина.
б) Пусть 
– бесконечно большая величина в точке . Докажем, что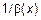 
– бесконечно малая величина. По определению 
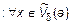
, или 
. Примем 
, тогда 
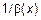, т. е. – бесконечно малая величина.
Следствие!
При нахождении пределов можно делать замену 
.
Вопрос 5. Сравнение бесконечно малых величин
Пусть и – бесконечно малые величины в точке 
. Для сравнения этих величин находят
. (3)
Теорема 5.
Предел отношения бесконечно малых величин в некоторой точке равен пределу отношения эквивалентных им бесконечно малых величин в этой точке. Если ~ 
и ~ 
, то
.
Доказательство.
= 
= 
= 
.
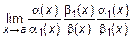Следствие!
В частности, если 
, то говорят, что величины эквивалентны ~ . При нахождении пределов их можно заменять (см. т. 5).
ПРИМЕР 3.
, поскольку 
и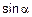 
~ 
.
Заключение
В большей части курса математики будем пользоваться множеством действительных чисел, которое обладает свойством непрерывности, плотности и упорядоченности, то есть математическим представлением восприятия окружающего пространства.
Отметим, что:
- бесконечно малая и бесконечно большая величины это функции;
- предел бесконечно малой величины в точке равен нулю;
- предел бесконечно большой величины есть бесконечность 
;
- сумма бесконечно малых величин есть бесконечно малая величина;
- бесконечно большая и бесконечно малая величины связаны между собой однозначным обратно пропорциональным преобразованием;
- величины бывают разного порядка малости, т. е. скорость убывания бесконечно малых функций может быть различна;
- сравнение бесконечно малых величин происходит на основании определения предела их отношения;
- в пределах можно переходить от бесконечно малых к бесконечно большим величинам.
Литература
1. Бермант А.Ф. и др. Краткий курс математического анализа. – М.: Высшая школа, 2001.
2. Натансон И.П. «Теория функций вещественной переменной». – СПб.: Лань, 1999, - 560 с.