Пусть функция 
определена на некотором интервале 
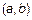. Осуществим следующие операции:
- аргументу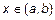 
дадим приращение 
: 
;
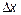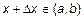- найдем приращение функции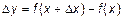 
;
- составим отношение приращения функции к аргументу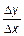 
;
- найдем предел этого отношения при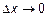 
: 
.
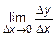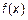и обозначают одним символом 
.
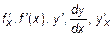Определение 3.
Производной функции в точке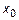 
называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
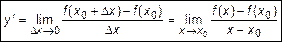. (4)
Замечание!
Производная функции есть некоторая функция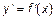 
, произведенная из данной функции.
Определение 4.
Функция , имеющая производную в каждой точке интервала 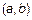, называется дифференцируемой в этом интервале, а операция нахождения производной функции называется дифференцированием.
Значение производной функции в точке 
обозначается одним из символов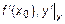 
или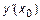 
.
ПРИМЕР 1.
Найти производную функции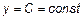 
.
Решение:
- аргументу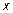 
дадим приращение ;
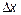- приращение функции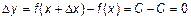 
;
- составим отношение 
;
- найдем предел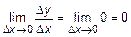 
, т. е. 
.
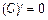ПРИМЕР 2. Найти производную функции 
.
Решение:
- аргументу 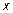дадим приращение ;
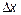- найдем соответствующее приращение функции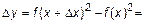 
;
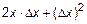- составим отношение 
;
- найдем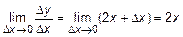 
или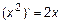 
.
Вернемся к перемещению точки. Было получено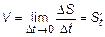 
.
Скорость прямолинейного движения материальной точки в момент времени t есть производная от пути по времени. В этом заключается физический смысл производной.
Другими словами, производная показывает, во сколько раз быстрее возрастает значение функции по отношению к росту переменной, или какова мгновенная скорость протекания процесса, описываемого некоторой функцией.
Вернемся к задаче с касательной к кривой. Был найден угловой коэффициент касательной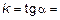 
.
Замечание!
То есть производная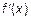 
в точке x равна угловому коэффициенту касательной к графику функции в точке, абсцисса которой, равна x. В этом заключается геометрический смысл производной.
2.2. Уравнение касательной и нормали к кривой
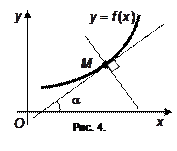Если точка касания M имеет координаты 
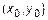(рис. 4), то угловой коэффициент касательной есть 
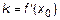. Воспользуемся уравнением прямой, проходящей через заданную точку в заданном направлении
. (5)
Определение 2.
Прямая, перпендикулярная касательной в точке касания, называется нормалью к кривой.
Нормаль перпендикулярна касательной, то ее угловой коэффициент
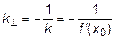. (6)
Поэтому уравнение нормали будет иметь вид (при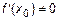 
)
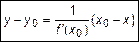. (7)
Теорема 1.
Если имеет предел А, то ее можно представить как сумму числа А и БМВ, т. е.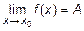 
, то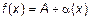 
.
Теорема 2.
Если функция дифференцируема в некоторой точке, то она непрерывна в ней.
Доказательство.
Пусть функция дифференцируема в некоторой точке x. Следовательно, существует предел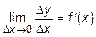 
. Отсюда имеем 
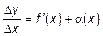, где 
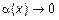при 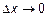, то есть 
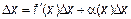. Переходя к пределу при 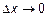, получаем 
. Это означает, что функция непрерывна в точке x.
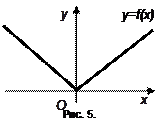Замечание!
Обратная теорема не верна. Непрерывная функция может не иметь производной. Пример: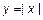 
в точке 
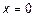(рис. 5).
Замечание!
Производная непрерывной функции сама необязательно является непрерывной.
Определение 3.
Если функция имеет непрерывную производную 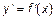на некотором интервале 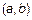, то функция называется гладкой.
Заключение
Отметим наиболее важные моменты:
- производная непрерывной функции необязательно непрерывна;
- если функция дифференцируема в некоторой точке, то она непрерывна в ней;
- функция, дифференцируемая в некоторой точке, не обязательно непрерывна;
- тангенс угла наклона определяет уравнение касательной и нормали к кривой.
Литература
1. Баврин И.И. Высшая математика. – М.: Просвещение, 1980. – 384 с.
2. Демидович Б.П., Кудрявцев В.А. Краткий курс высшей математики. – М.: Астрель, 2001. - 656 с.
Лекция 7. Правила дифференцирования функции
Цель лекции: изучить правила дифференцирования функций; научиться применять эти правила при решении прикладных задач.
План лекции