Пусть {\displaystyle A} 
— матрица размера {\displaystyle m\times n} 
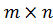над полем {\displaystyle C} 
(или {\displaystyle R} 
). Пусть {\displaystyle T} 
— линейное преобразование, соответствующее {\displaystyle A} в стандартном базисе; это значит, что {\displaystyle T(x)=Ax} 
. Ранг матрицы {\displaystyle A} — это размерность области значений преобразования {\displaystyle T} .
Методы:
Существует несколько методов нахождения ранга матрицы:
· Метод элементарных преобразований
Ранг матрицы равен числу ненулевых строк в матрице после приведения её к ступенчатой форме при помощи элементарных преобразований над строками матрицы.
· Метод окаймляющих миноров
Пусть в матрице {\displaystyle A} найден ненулевой минорно{\displaystyle k}го порядка {\displaystyle M} 
. Рассмотрим все миноры {\displaystyle (k+1)}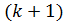 
-го порядка, включающие в себя (окаймляющие) минор {\displaystyle M} ; если все они равны нулю, то ранг матрицы равен {\displaystyle k} 
. В противном случае среди окаймляющих миноров найдется ненулевой, и вся процедура повторяется.
След матрицы
След матрицы — операция, отображающая пространство квадратных матриц в поле, над которым определена матрица (для действительных матриц — в поле действительных чисел, для комплексных матриц — в поле комплексных чисел). След матрицы — это сумма элементов главной диагонали матрицы, то есть если 
{\displaystyle a_{ij}} элементы матрицы {\displaystyle A}A, то её след {\displaystyle {\mathop {\rm {tr}}}\;A=\sum _{i}a_{ii}} 
.
В математических текстах встречается два обозначения операции взятия следа: {\displaystyle {\mathop {\rm {Tr}}}\;A} 
(от англ. trace — след), и {\displaystyle {\mathop {\rm {Sp}}}\;A} 
(от нем. Spur — след).
Свойства
· Линейность {\displaystyle {\mathop {\rm {tr}}}\;(\alpha A+\beta B)=\alpha {\mathop {\rm {tr}}}\;A+\beta {\mathop {\rm {tr}}}\;B} 
.
· {\displaystyle {\mathop {\rm {tr}}}\;(AB)={\mathop {\rm {tr}}}\;(BA)} 
.
Следствие: след одинаков для всех подобных матриц: {\displaystyle \mathop {\rm {tr}} \;(C^{-1}AC)=\mathop {\rm {tr}} \;A} 
.
· {\displaystyle {\mathop {\rm {tr}}}\;A={\mathop {\rm {tr}}}\;A^{\mathrm {T} }} 
, где {\displaystyle \mathrm {T} } означает операцию транспонирования.
· {\displaystyle \ln \det A={\mathop {\rm {tr}}}\;\ln A} 
.
· Если {\displaystyle A\otimes B} 
тензерное произведение матриц A и B, то {\displaystyle {\mathop {\rm {tr}}}\;A\otimes B=({\mathop {\rm {tr}}}\;A)({\mathop {\rm {tr}}}\;B)} 
.
· След матрицы равен сумме её собственных значений.
· Определитель квадратной матрицы {\displaystyle n\times n} 
можно выразить через следы степеней этой матрицы, не превосходящие {\displaystyle n} 
. Например {\displaystyle \det A_{3\times 3}={\frac {1}{6}}\left(({\mathop {\rm {tr}}}A)^{3}-3{\mathop {\rm {tr}}}A\cdot {\mathop {\rm {tr}}}A^{2}+2{\mathop {\rm {tr}}}A^{3}\right)} 
.
Геометрическое свойство
· {\displaystyle {\mathop {\rm {det}}}(E+G\varepsilon)=1+{\mathop {\rm {tr}}}G\ \varepsilon \ +o(\varepsilon)} 
,
где E — единичная матрица, ε — бесконечно малое число. То есть бесконечно малое линейное преобразование изменяет объём на величину, пропорциональную следу генератора этого преобразования в первом порядке по его малому параметру. Иными словами, скорость изменения объёма при таком преобразовании равна следу его генератора.
· Следствия:
· {\displaystyle {\mathop {\rm {det}}}\ {\mathop {\rm {exp}}}(G\alpha)=1+{\mathop {\rm {tr}}}G\ \alpha \ }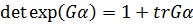 
для малых 
· Для того, чтобы преобразования не меняли объём, достаточно того, чтобы их генераторы были бесследовыми.
Применение матричных инвариантов для решения различных математических задач
Задача. Решить систему линейных уравнений.
Для начала посчитаем определители:
, значит решение у системы уравнений есть.
Воспользуемся формулами Крамера:
, 
,
,
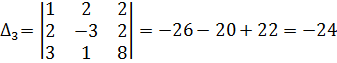Тогда 
, 
, 
.
Ответ 
.
Задача. Найдите ранг матрицы 
Решение. С помощью элементарных преобразований над строками матрицы, приведём ее к ступенчатому виду. Для этого вначале от третьей строки отнимем две вторых:
От второй строки отнимаем четвертую строку, умноженную на 4; от третьей - две четвертых:
Ко второй строке прибавим пять первых, к третьей- три третьих:
Меняем местами первую и вторую строки:
Далее четвертую и первую строки:
Ответ. 
.
Заключение
Таким образом, хочется сказать, что тема «Матричные инварианты» очень важна при изучении математики в целом. Определители, ранги матриц находят широкое применение во всем курсе алгебры, математического анализа, и, как было показано в пункте 3.1. затрагивают даже геометрию.
С помощью данных инвариантов, мы можем с легкостью решать ряд математических задач, таких как: системы линейных уравнений, нахождение площадей или объёмов фигур на плоскости, анализировать линейную зависимость(независимость) строк(столбцов) матриц.
Безусловно, мне, как студентке уже 3 курса, особых затруднений в изучении данная тема не вызвала. Всё было локанично, просто и доступно к изучению.
Литература
1. https://ru.wikipedia.org/wiki/Инвариант_(математика);
2. https://studfiles.net/preview/6126435/page:7/;
3. Курош А.Г. Курс высшей алгебры: Учебник. 16-е изд., стер.-СПб.: Издательство «Лань»; М.: Издательство «Физматкнига», 2007.-432с.: ил.; с. 37-43,70-77.
4. Баврин И.И. Высшая математика: Учеб. Для студ. естественно-научных специальностей педагогических вузов / Иван Иванович Баврин. – 4-e изд., испр. и доп.- М.: Издательский центр «Академия», 2004.-616 с; с. 68-74.
5. Белоусов И. В. Матрицы и определители: учебное пособие по линейной алгебре. Кишинев: 2006.91с; с.35-44.