Теорема.
Если все члены функционального ряда  аналитичны в односвязной области D и ряд сходится в D равномерно, то его можно почленно дифференцировать.
аналитичны в односвязной области D и ряд сходится в D равномерно, то его можно почленно дифференцировать.
Доказательство.
Пусть 
Поскольку такие ряды можно почленно интегрировать, то проинтегрируем (1) по замкнутому контуру  .
.

Применим теорему коши к интегралам 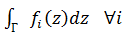 =>
=>
 , но s(z) непрерывна =>(по теореме Морера) s(z)- аналитическая функция=> бесконечно дифференцируема в D и справедливы формулы для производных
, но s(z) непрерывна =>(по теореме Морера) s(z)- аналитическая функция=> бесконечно дифференцируема в D и справедливы формулы для производных


Ряд  умножим слева и справа на
умножим слева и справа на 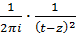


Или

Свойства степенных рядов в круге сходимости.
1. Равномерная сходимость в замкнутом круге из круга сходимости

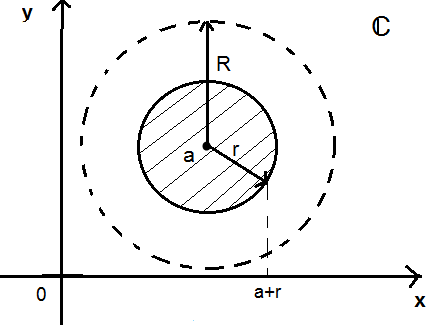 Пусть R>0
Пусть R>0 
Очевидно, что (a+r) лежит внутри круга сходимости


По свойствам круга сходимости в точке (a+r) ряд (1) сходится абсолютно, то есть 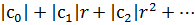 (2) абсолютно сходится.
(2) абсолютно сходится.

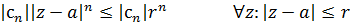 (для замкнутого круга)
(для замкнутого круга)
 можарируется рядом (2).
можарируется рядом (2).
По признаку Вейерштрасса (1) абсолютно и равномерно сходится в заштрихованном круге.
Следствие 1. Сумма ряда (1) непрерывны внутри круга сходимости.
2. Аналитичность суммы ряда внутри круга сходимости
a) Замкнутый круг  – односвязная область.
– односвязная область.
b) Функции  непрерывны в этом круге. Сходимость равномерная => ряд можно почленно дифференцировать в круге
непрерывны в этом круге. Сходимость равномерная => ряд можно почленно дифференцировать в круге

Таким образом сумма этого степенного ряда  непрерывна. Следовательно s(z) аналитична внутри круга сходимости.
непрерывна. Следовательно s(z) аналитична внутри круга сходимости.

3.  Следствие. Степенной ряд можно бесконечное число раз дифференцировать внутри круга сходимости.
Следствие. Степенной ряд можно бесконечное число раз дифференцировать внутри круга сходимости.
4. Степенной ряд можно интегрировать почленно вдоль любой кривой принадлежащей кругу сходимости.
В замкнутом круге охватывающий Г s(z) равномерно непрерывна и члены ряда непрерывные функции.
Проинтегрируем (1) по  (соеденим точку а с точкой z внутри круга)
(соеденим точку а с точкой z внутри круга)

Ряд Тейлора.
Единственность разложения функции в степенной ряд.
Ранее доказано, что аналитическую функцию в D можно разложить в степенной ряд.



=> 
Определение.
Если  аналитична в точке а, то ряд
аналитична в точке а, то ряд

Называется рядом Тейлора f(z) с центром разложения в точке а.
Различные определения аналитичной функции и их эквивалентность
Определение 1.
Функция f(z) называется аналитичной в области D, если она дифференцируема в D.
Определение 2.
Функция f(z) аналитична в D, если она имеет непрерывную производную в D.
Определение 3.
Функция f(z) аналитична в D, если ее действительная и мнимая части сопряженные гармонические функции в D.
Определение 4.
Функция f(z) аналитична в D, если для любой точки а  f(z) раскладывается в степенной ряд в окрестности этой точки
f(z) раскладывается в степенной ряд в окрестности этой точки

Определение 4.
Функция f(z) аналитична в D, если непрерывна в D и  , Г – кусочно-гладкий.
, Г – кусочно-гладкий.
Все 5 определений эквиваленты.
Свойства единственности аналитической функции.
Теорема.
Если значения двух функций, аналитический в области D совпадают на последовательности точек  и сходятся к точке а
и сходятся к точке а  , то эти функции совпадают во всех точках
, то эти функции совпадают во всех точках  .
.
Доказательство.
1.  круг с центром в точке а.
круг с центром в точке а. 

В силу аналитичности f(z) и g(z) в D


Аналитичные функции непрерывны в D => f,g непрерывны в точке а
Так как  =>
=>


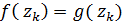 по условию =>
по условию => 






И так далее  =>
=> 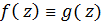 в D.
в D.
2. Область D произвольного типа.
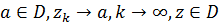
Докажем, что  . Соединим точку z с точкой а кривой Жордана.
. Соединим точку z с точкой а кривой Жордана.


Дугу АВ А(а) В(z) разобьем на части с длинами меньше d с помощью точек 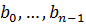 , где
, где 
Строим круги  .
.  захватывают точки
захватывают точки 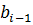 и
и  . С помощь этих кругов закроем всю кривую.
. С помощь этих кругов закроем всю кривую.
Рассмотрим круг 
Очевидно, что элементы последовательности  , начиная с некоторого номера попадают туда. Сам круг содержится в D
, начиная с некоторого номера попадают туда. Сам круг содержится в D
Можно применять первый случай =>
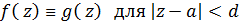
Поскольку первый круг пересекается по области со вторым кругом и точка  принадлежит пересечению, то
принадлежит пересечению, то

 . Причем
. Причем  на втором круге.
на втором круге.

 на последнем круге
на последнем круге
Таким образом f и g совпали и в точке z => 
Ч.т.д.
Теорема.
Пусть  и
и 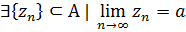 , где
, где  то тошда, если у функции
то тошда, если у функции 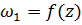 определенный на А есть аналитическое продолжение в D, то оно единственное.
определенный на А есть аналитическое продолжение в D, то оно единственное.
Понятие полного аналитического продолжения.
 определена на
определена на  и аналитически продолжена на
и аналитически продолжена на  получим
получим  далее продолжим
далее продолжим  на
на  и так далее.
и так далее.
Процесс идет до тех пор, пока можно продолжать. Получим полное аналитическое продолжение.
Нули аналитической функции. Кратность нуля.
Определение 1.
Число а называется нулем функции  , если
, если  .
.
Для случая многочленов от вещественно переменной известно, что число а есть корень кратности k для многочлена  , если
, если

Аналогично вводится понятие для комплексного случая  .
.
Определение 2.
Если f аналитична в точке а и f(a)=0, то точка а называется нулем кратности k, если в некоторой окрестности этой точки

Пример.
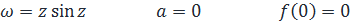

Таким образом, к=2.
Теорема 1.
Если  аналитична в точке а и f(a)=0, то найдется такая окрестность точки а и такая функция
аналитична в точке а и f(a)=0, то найдется такая окрестность точки а и такая функция  , что
, что

Доказательство.
В силу аналитичности f в точке а ее можно разложить в степенной ряд по степеням(z-a) в некоторой окрестности точки а



Пусть  и для которого
и для которого  и
и 
Тогда


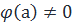 , так как
, так как 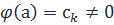
Ч.т.д.
Теорема 2.
Число будет тогда и только тогда нулем кратности k, аналитична в точке 0 функции, когда

Доказательство.


Ч.т.д.
Пример.
 - аналитическая в точке
- аналитическая в точке  .
.
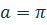



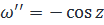

Таким образом, кратность k=2.
Определение 3.
Точка а называется изолированным нулем функции f(z), если f(a)=0, но существует окрестность точки а в которой других нулей функции нет.
Следствие.
Аналитическая в области D функция не равная тождественно 0 в D имеет в D только изолированные нули.
Если бы функция имела в D неизолированные 0, то нашлась бы последовательность  что
что 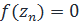 и
и  . В силу аналитичности
. В силу аналитичности  на D.
на D.
Ряд Лорана
Рассмотрим ряд
 Пусть
Пусть 
(1)=>  (2)
(2)
Пусть R – радиус окружности ряда (2)
1) 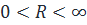 (2) сходится абсолютно на
(2) сходится абсолютно на  или
или 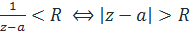 .
.
 – радиус окружности ряда(1).
– радиус окружности ряда(1).
2)  , тогда (2) сходится при
, тогда (2) сходится при  , но
, но  область окружности ряда (1)
область окружности ряда (1)  . (1) расходится на
. (1) расходится на  .
.
3)  , тогда(2) сходится на
, тогда(2) сходится на  (1) сходится
(1) сходится 
 .
.
Свойства суммы ряда в области сходимости:
1. Ряд абсолютно сходится внутри области сходимости.
2. Ряд равномерно сходится на множествах

3. Сумма ряда (1) аналитична в области сходимости.
Рассмотрим (3)  и (4)
и (4) 
(3)+(4)= 
В силу абсолютной сходимости в своих областях сходимости суммирование членов можно производить в любом порядке.

 Найдем область сходимости (5). Очевидно, что это есть пересечение областей сходимости (3) и (4)
Найдем область сходимости (5). Очевидно, что это есть пересечение областей сходимости (3) и (4)
a) R – радиус сходимости (3); r – радиус сходимости (4).

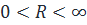


b)  . Область сходимости
. Область сходимости 
c) 
d) 
 - проколотая плоскость
- проколотая плоскость 
Свойства ряда (5) аналогичны 1 – 3 свойствам предыдущего ряда.
Определение.
Ряд (3) называется правильной частью ряда (5), (4) – главная часть ряда (5).
 Пример.
Пример.

 - геометрическая прогрессия
- геометрическая прогрессия  .
.

Разложение функции в ряд Лорана.
Пусть функция определена в круговом кольце  и раскладывается в ряд
и раскладывается в ряд  в этом кольце. Найдем
в этом кольце. Найдем 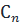 .
.
На С ряд сходится равномерно, его члены аналитичны и ряд можно почленно интегрировать.

Можно показать  , при n≠
, при n≠  1
1  - окружность.
- окружность.
Тогда 

При  имеем
имеем  , тогда
, тогда

 . Тогда
. Тогда


Из (*) следует, что функцию единственным образом можно представить в виде суммы ряда Ларана.
Теорема.
Если функция аналитична в кольце  , то ее ряд лорана по степеням
, то ее ряд лорана по степеням 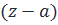 сходится к ней в этом кольце.
сходится к ней в этом кольце.