КУРСОВАЯ РАБОТА
Выполнил:
студент 3 курса очной формы обучения
Данилова Юлия Аркадьевна
Руководитель: дфмн, проф.Хэкало Сергей Павлович
Итоговая оценка - ______
Подпись______
Коломна – 2017 г.
Оглавление
1. Введение_________________________________________________3
2. Понятие интеграла по комплексной переменной________________4
3. Теорема Коши__________________________________________9
4. Интегрирование функциональных рядов____________________22
5. Неравенства для  _________________________________________26
_________________________________________26
6. Дифференцирование функциональных рядов_________________33
7. Ряд Тейлора___________________________________________36
8. Ряд Лорана____________________________________________43
9. Изолированные особые точки однозначного характера________46
10. Заключение____________________________________________52
11. Список используемой литературы__________________________53
Введение
Теория функций комплексного переменного это раздел математического анализа, в котором рассматриваются и изучаются функции комплексного аргумента. Знакомство с основными вопросами данной теории, бесспорно, являются необходимым элементом математического образования. В данной работе я хочу освятить такую тему как, классификация особых точек функции комплексного переменного. Для этого необходимо рассмотреть такой раздел, как дифференциальное и интегральное исчисления функции комплексного переменного.
Понятие интеграла по комплексной переменной
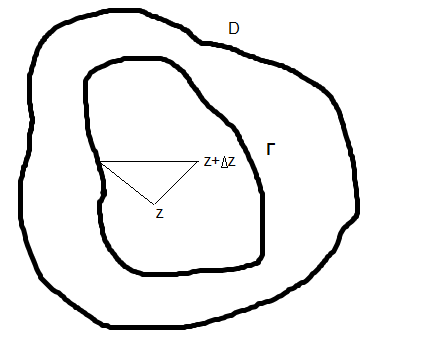
Пусть Г- кусочно-гладкая кривая

 , где
, где  непрерывны, кроме конечного числа точек
непрерывны, кроме конечного числа точек 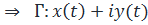 ,
, 


Пусть функция  определена на Г.
определена на Г.
Составим интегральные суммы следующим образом:
Ориентируем Г(считаем  Пусть Т- разбиение
Пусть Т- разбиение 
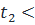 …
…  .
.
Возьмем произвольную  и
и  Составим интегральные суммы
Составим интегральные суммы


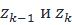 .
.  - соответствует вектору
- соответствует вектору 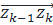 . Для кусочно-гладкой кривой длина дуги
. Для кусочно-гладкой кривой длина дуги 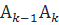 эквивалентна
эквивалентна  при
при 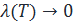 (
( ).
).
Таким образом, в определении комплексного интеграла безразлично, что устремлять к нулю.
Определение.
Если конечный 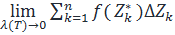 не зависит от способа разбиения и от способа выбора
не зависит от способа разбиения и от способа выбора  , то он называется интегралом функции f(z) по Г
, то он называется интегралом функции f(z) по Г

Свяжем этот интеграл с криволинейным интегралом II рода.

На  . Обозначим
. Обозначим  ,
,  ,
, 


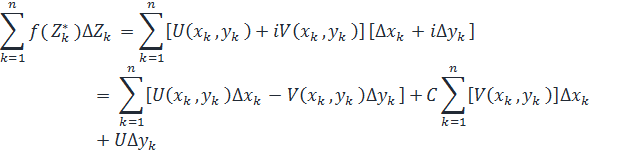
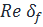 есть интегральные суммы для
есть интегральные суммы для

 есть интегральные суммы для
есть интегральные суммы для

Т.о.



Следствие
Если  непрерывна на Г, то интеграл существует
непрерывна на Г, то интеграл существует
Свойства 
1.  ,
, 
2. 
3. 
4.  ,
, 
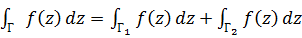
5. 
Доказательство

Перейдем к lim, имеем:

Для непрерывной функции f(z) на Г пусть
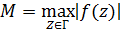
По  имеем
имеем 
6. Замена переменной в комплексном интеграле
Пусть функция 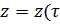 )
) 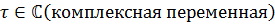

 )- аналитическая функция
)- аналитическая функция
 ) – интегрируема на Г
) – интегрируема на Г 

Если С=[c;d] – отрезок
 , то
, то


 Пример 1.
Пример 1.


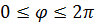




При обходе по  получим
получим 
Пример 2.
 , где С соединяет т.
, где С соединяет т.  и
и 

 – интеграл не зависит от пути
– интеграл не зависит от пути
Пример 3.
 Г- радиус вектор т.
Г- радиус вектор т. 
OA: O(0;0) A(3;-4)









Теорема Коши
Вспомнил формулу Грина для односвязной области, ограниченной замкнутым кусочно-гладким контуром в случае непрерывности функций


Теорема Коши
Пусть D – односвязная область в  .
.  - аналитическая в D, тогда для любого замкнутого кусочно-гладкого контура
- аналитическая в D, тогда для любого замкнутого кусочно-гладкого контура  справедливо
справедливо

Свойство. Аналитичность f означает, что она имеет непрерывную производную в окрестности каждой точки из D

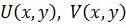 имеют непрерывные частные производные
имеют непрерывные частные производные  и справедливы условия Коши-Римана
и справедливы условия Коши-Римана 
 – интегрируема как аналитическая и справедливо
– интегрируема как аналитическая и справедливо


G- область, ограниченная Г, 


Ч.т.д.
Обобщение теоремы Коши
Пусть 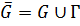 – замкнутая односвязная область.
– замкнутая односвязная область.  непрерывна на Г и аналитична на G, тогда
непрерывна на Г и аналитична на G, тогда

Распространение теоремы Коши на сложный контур
Определение.
Пусть G- область. Рассмотрим границу этой области, составленную из (n+1) кривой 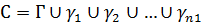 , все они кусочно-гладкие, замкнутые и
, все они кусочно-гладкие, замкнутые и
1) Г содержит все  (внутри себя)
(внутри себя)
2) Каждое  лежит во внешности
лежит во внешности  , при
, при 


Теорема Коши.
Если  непрерывна на границе области G ограниченной сложным контуром С
непрерывна на границе области G ограниченной сложным контуром С  , аналитична внутри, то
, аналитична внутри, то


Доказательство.

 Сделаем область G односвязной с помощью разрезов. Для этого соединим
Сделаем область G односвязной с помощью разрезов. Для этого соединим  с Г кривыми. Делаем разрез по
с Г кривыми. Делаем разрез по  , отметим ориентацию. В силу сделанных разрезов стал невозможен обход вокруг каждой дырки.
, отметим ориентацию. В силу сделанных разрезов стал невозможен обход вокруг каждой дырки.
Можно применять следствие к теореме Коши (т.к. область стала односвязной) для контура.

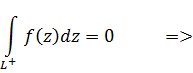



Причем

Ч.т.д.
 Следствия
Следствия


Поэтому для удобства вычисления в роли внутреннего контура берут окружности.
Первообразная функция комплексного переменного в односвязной области.
Пусть  аналитична в односвязной области G. По теореме Коши для любого кусочно-гладкого контура
аналитична в односвязной области G. По теореме Коши для любого кусочно-гладкого контура 


Интеграл берется по кусочно-гладкой кривой  . Интеграл не зависит от пути интегрирования, а зависит только от положительной точки Z.
. Интеграл не зависит от пути интегрирования, а зависит только от положительной точки Z.
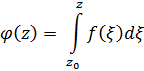
Такой же вывод мы получим, если заменим требования аналитичности  на:
на:
1)  ;
;
2) для любого кучно-гладкого контура Г, лежащего внутри G

Теорема.
Пусть  определена, непрерывна в односвязной области G, для любого замкнутого кучно-гладкого контура
определена, непрерывна в односвязной области G, для любого замкнутого кучно-гладкого контура  ,
, 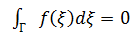 . Тогда функция
. Тогда функция  дифференцируема на G и
дифференцируема на G и  .
.
Доказательство.
Докажем, что 
Пусть  ,
,  . Ищем
. Ищем 







 непрерывна в точке z =>
непрерывна в точке z =>
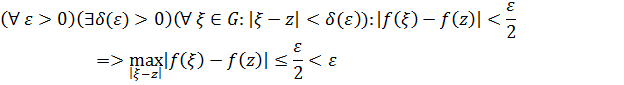
Очевидно, что найденное  – искомое, так как
– искомое, так как
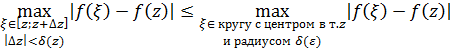
ч.т.д.
Следствие. Если f(z) аналитична в G, то  в G, где
в G, где 
Пример.



Определение. Первообразной функции  является
является  в области G, если
в области G, если  в G.
в G.
Для односвязных областей и аналитичных функций существует первообразные.
Лемма.
Если  в области
в области  , то f
, то f  в D.
в D.
 аналитична в D, т. К. имеет непрерывную производную
аналитична в D, т. К. имеет непрерывную производную  =>
=>






 , аналогично
, аналогично 
Теорема.
Если  некоторая первообразная для f(z) на D, то множество всех первообразных описываются формулой:
некоторая первообразная для f(z) на D, то множество всех первообразных описываются формулой:

Определение. Неопределенным интегралом для функции f(z) в области D называется совокупность всех первообразных указанной функции в области D.

Теорема.
Если функция f(z) аналитична в односвязной области D, то

Доказательство.

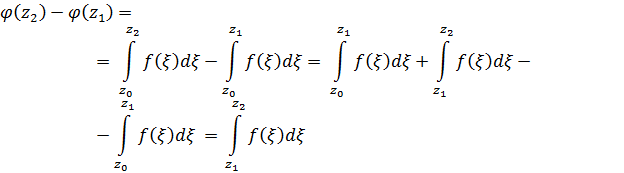
В силу леммы формула верна для любой другой первообразной.
Ч.т.д.
Пример.

Интеграл как функция точки в многосвязной области.
G – многосвязная область
f(z) непрерывна на G и существует замкнутый контур Г в G, что  .
.
Покажем, что тогда  , где
, где 

 и
и  соединим кусочно-гладкой прямой. Есть многозначная функция, значение которой зависит от формы пути.
соединим кусочно-гладкой прямой. Есть многозначная функция, значение которой зависит от формы пути.
Соединим  и
и  двумя путями.
двумя путями.




Рассмотрим

 , где интеграл берется по любому пути из точки 1 в точку z через точку 0.
, где интеграл берется по любому пути из точки 1 в точку z через точку 0.
Пусть путь из точки 1 в точку z не охватывает точку о.
 - было подсчитано
- было подсчитано
 Посчитаем по-другому. Г лежит в области, где
Посчитаем по-другому. Г лежит в области, где  . Аналитично следует, что
. Аналитично следует, что  не зависит от формы пути.
не зависит от формы пути.
Заменим Г на следующий путь







Рассмотрим сложный контур ( )
)
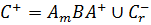
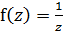 аналитична внутри и на границе области, ограниченной этим контуром.
аналитична внутри и на границе области, ограниченной этим контуром.
 По теореме Коши для сложного контура
По теореме Коши для сложного контура


Т.о. для произвольных контуров, не проходящих через точку О, получим
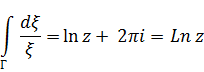
Интеграл Коши
Установим связь между значениями аналитичной функции во внутренних точках области ее аналитичности и граничными значениями этой функции.
Теорема
Пусть  аналитична в односвязной области G ограниченной контуром C. Точка а лежит в G. Г- замкнутый, кусочно-гладкий контур, охватывающий а,
аналитична в односвязной области G ограниченной контуром C. Точка а лежит в G. Г- замкнутый, кусочно-гладкий контур, охватывающий а,  . Тогда справедлива формула:
. Тогда справедлива формула:

Доказательство.
 существует, так как
существует, так как  тоже аналитична =>
тоже аналитична =>  – аналитична.
– аналитична.


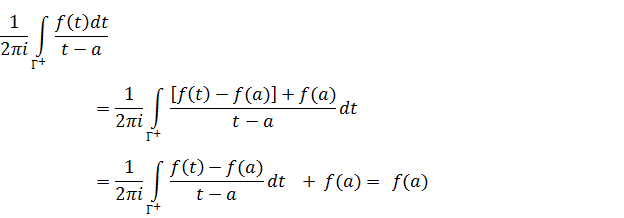
Тогда и только тогда, когда 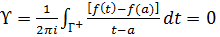 (*)
(*)
Проверим это. Пусть  убедимся, что
убедимся, что 
Вместо  , где
, где  лежит внутри Г.
лежит внутри Г.

Из непрерывности f(z) в точке а =>

Пусть 
Ч.т.д.
Замечание.
1) Формула называется интегральна формулой Коши.
2) Формулу можно применять, в случае, когда f(z) непрерывна на Г и аналитична внутри. Можно применять в многосвязных областях, если Г сложный контур.
Пример.
Вычислить 
а=0 
 охватывает точку 0.
охватывает точку 0.
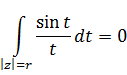


Следствие. Если две аналитических функции совпадают на границе области аналитичности, то они равны и внутри этой области.
Интегрирование функциональных рядов
Рассмотрим функциональный ряд.

Ряд называется равномерносходящимся на Е, к сумме S(z)

Справедлив критерий равномерной сходимости
Критерий.
Ряд  равномерно сходится тогда и только тогда, когда
равномерно сходится тогда и только тогда, когда 

Признак Вейерштрасса
Ряд  равномерно сходится на Е, если существует положительный числовой ряд
равномерно сходится на Е, если существует положительный числовой ряд  , такой что
, такой что

Теорема.
Если члены функционального ряда 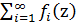 непрерывны на кусочно-гладкой кривой L и если ряд равномерно сходится на L, то его можно почленно интегрировать на L
непрерывны на кусочно-гладкой кривой L и если ряд равномерно сходится на L, то его можно почленно интегрировать на L

Доказательство.
Все написанные интегралы существуют в силу непрерывности  и непрерывности
и непрерывности  .
.
Докажем, что 


Ищем номер.

Так как ряд равномерно сходится на L =>  равномерно сходится к S(z) на L.
равномерно сходится к S(z) на L.



Найденный номер искомый.
Разложение аналитической функции в степенной ряд.
Теорема.
Аналитическую в области G функцию можно разложить в степенной ряд в окрестности любой точки 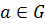 .
.
Разложение справедливо в круге, радиус которого равен расстоянию от точки а до границы G.
Доказательство
Покажем, что для любого z принадлежащего внутренности круга

Воспользуемся интегральной формулой Коши

Рассмотрим функцию  разложим ее по степеням (z-a)
разложим ее по степеням (z-a)




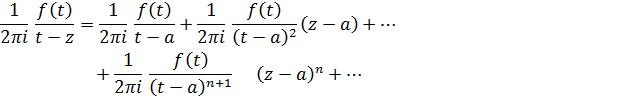
Получившийся ряд можно почленно интегрировать по  (члены ряда, как функции от t будут непрерывны на
(члены ряда, как функции от t будут непрерывны на  , так как f(t) непрерывна(аналитична) и
, так как f(t) непрерывна(аналитична) и  непрерывна на
непрерывна на  )
)
Проверим равномерную сходимость на контуре(по теореме Вейерштрасса)

 сходится
сходится  . Таким образом наш ряд (*) сходится равномерно.
. Таким образом наш ряд (*) сходится равномерно.
Интегрируемый ряд (*)

Таким образом

Где 
Ч.т.д.
Замечание.
В формулах для  интеграл не зависит от вида кривой.
интеграл не зависит от вида кривой.
Неравенства для 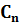
Теорема Лиувилля. Основная теорема алгебры.
Оценим коэффициенты разложения функции в степенной ряд.

 Минимальное расстояние от т. А до границы G
Минимальное расстояние от т. А до границы G
Теорема Лиувилля.
Если функция  является аналитической на
является аналитической на  и ограничена на
и ограничена на  , то эта функция постоянна.
, то эта функция постоянна.
Доказательство.
Пусть 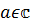 (фиксируем) и разложим функцию f(z) по степеням
(фиксируем) и разложим функцию f(z) по степеням 
 . где разложение верно на
. где разложение верно на 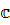 .
.
Так как функция ограниченна на 
 /
/
 . Здесь r любое число
. Здесь r любое число
Если 

Ч.т.д.
Основная теорема алгебры.
Всякое алгебраическое уравнение с комплексными коэффициентами имеет по крайней мере один корень.

Доказательство.
Рассмотрим  . Доказательство проведем методом от противного.
. Доказательство проведем методом от противного.
Пусть  .
. 
 аналитична на
аналитична на  .
.
Покажем, что 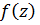 ограниченная функция на всей плоскости.
ограниченная функция на всей плоскости.

 по свойствам пределов функций
по свойствам пределов функций  в которой
в которой 


На оставшемся множестве  и как на компакте непрерывная функция
и как на компакте непрерывная функция  ограничена.
ограничена.

 кругу.
кругу.
Значит,  ограничена на
ограничена на  .
.

По теореме Лиувилля  – число, сто противоречит свойствам
– число, сто противоречит свойствам 
Таким образом предположение не верно и наше уравнение имеет по крайней мере один комплексный корень.
Интегральные формулы для производных аналитических функций. Теорема Морера.
Пользуясь интегральной формулой Коши  , докажем теорему.
, докажем теорему.
Теорема.
Аналитическая в односвязной области D функция и на ее границе имеет в каждой точке области производные всех порядков, значение которых определяются по формуле Коши.

Доказательство.
 Проведем для n=1, далее по методу индукции.
Проведем для n=1, далее по методу индукции.

 , берем так, чтобы
, берем так, чтобы 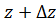 лежали внутри.
лежали внутри.



 .
.
Пусть 
 . Считаем, что
. Считаем, что 
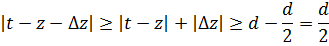
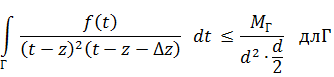
Ч.т.д.
Следствие 1.
Если функция аналитична в точке z, то она имеет в точке z производные всех порядков.
Следствие 2.
Если f аналитична в области G, то и все ее производные аналитичны в области G.
Пример.



a)Г: 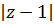 =2
=2
б) Г:  =1
=1

 ;
;  ; n=2; f(t)- аналитична на
; n=2; f(t)- аналитична на  .
.

Если Г охватывает точку 
 , если Г не охватывает точку
, если Г не охватывает точку 

 а) б)
а) б)
Теорема Морера.
Теорема.
Если функция f(z) непрерывна в односвязной области и  , то f(z) аналитична в D.
, то f(z) аналитична в D.
Доказательство.
Было доказано ранее, что интеграл от f(z) по кусочно-гладким кривым из D не зависит от формы пути, а функция 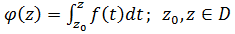 , будет аналитической функцией и
, будет аналитической функцией и  .
.
 - есть аналитическая функция.
- есть аналитическая функция.
Ч.т.д.
Примеры.
Доказано 
 - кусочно-гладкий, замкнутый контур, охватывающий точку z.
- кусочно-гладкий, замкнутый контур, охватывающий точку z.
 Вычислить
Вычислить  ,
, 

a=i, n+1=0 => n=1; f(z)=