Применение компьютерных экспериментов при изучении геометрии позволяет активизировать познавательную деятельность учащихся, реализовывая на уроке идеи исследовательского обучения. Простота исследований, проводимых с помощью компьютерного эксперимента, позволяет создавать ситуацию успеха для тех учащихся, кто не слишком искушен в математических выкладках, при этом повышается их учебная мотивация, формируется уверенность в собственных силах и в целом изменяется отношение к математике.
Федеральные государственные образовательные стандарты основного общего образования третьего поколения определяют повышенные требования к компьютерной поддержке процесса обучения. В частности, «...предметные результаты изучения предметной области "Математика и информатика" должны отражать: <…> 9) развитие умений применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, компьютера, пользоваться оценкой и прикидкой при практических расчётах; 10) формирование информационной и алгоритмической культуры; формирование представления о компьютере как универсальном устройстве обработки информации; развитие основных навыков и умений использования компьютерных устройств…» [5, с. 11 ].
Возможность удовлетворения этому требованию стандарта при обучении геометрии обеспечивается специализированным программным обеспечением – интерактивными геометрическими средами (ИГС): GeoGebra, GeoNext, «Живая математика», «Математический конструктор», а также создаваемыми на основе этого программного обеспечения цифровыми образовательными ресурсами (ЦОР). Достоинством названного программного обеспечения и основанных на нем ЦОР является интерактивность, т.е. возможность не только внесения пользователем начальных данных для построения изображения геометрической конфигурации, но их параметризация с последующим изменением при сохранении общего алгоритма построения чертежа, а также возможность оперативного получения интересующих пользователя сведений о свойствах изображенных фигур. Свойство интерактивности позволяет рассматривать ИГС как виртуальные динамические лаборатории, используемые учащимися для проведения исследований на уроках и во внеурочное время с привлечением эмпирических методов научного познания: наблюдений, опытов, экспериментов.
Данные программы предоставляют еще один вариант проведения практического занятия. Но практическое занятие с использованием интерактивных геометрических сред (ИГС): GeoGebra, GeoNext, «Живая математика», «Математический конструктор» будет иметь более экспериментальный и исследовательский характер, нежели иметь практическую направленность.
Рассмотрим подробней некоторые интерактивные геометрические среды.
GeoGebra 3D – это свободная образовательная математическая программа, соединяющая в себе геометрию, алгебру и математические исчисления. GeoGebra 3D – свободно-распространяемая (GPL) динамическая геометрическая среда, которая даёт возможность создавать «живые чертежи» в планиметрии, стереометрии, в частности, для построений с помощью циркуля и линейки.
Переведена на 39 языков. Полностью поддерживает русский язык. Программная среда GeoGebra3D может быть быстро освоена людьми, имеющими элементарные навыки работы на компьютере, что, несомненно, является большим преимуществом данного программного продукта. К еще одному аргументу в пользу GeoGebra 3D можно отнести её простую интеграцию с офисными приложениями – все чертежи легко могут через буфер обмена быть перенесены для дальнейшего использования как в текстовые редакторы, поддерживающие работу с изображениями, так и в графические редакторы.
Возможности GeoGebra 3D
1. Построение графиков функций {\displaystyle y=f(x)};
· Построение кривых, заданных параметрически в декартовой системе координат: {\displaystyle x=f(t);y=g(t)};
· Построение конических сечений:
· Коника произвольного вида — по пяти точкам.
· Окружность:
— по центру и точке на ней;
— по центру и радиусу;
— по трем точкам;
· Эллипс — по двум Фокусам и точке на кривой;
· Парабола — по фокусу и директрисе;
· Гипербола — по двум фокусам и точке на кривой.
· Построение геометрического места точек, зависящих от положения некоторой другой точки, принадлежащей какой-либо кривой или многоугольнику (инструмент Локус).
2. Вычисления
· Действия с матрицами:
Ø Сложение, умножение;
Ø Транспонирование, инвертирование;
Ø Вычисление определителя;
· Вычисления с комплексными числами;
· Нахождение точек пересечения кривых;
· Статистические функции:
Ø Вычисление математического ожидания, дисперсии;
Ø Вычисление коэффициента корреляции;
· Аппроксимация множества точек кривой заданного вида:
Ø полином,
Ø экспонента,
Ø логарифм,
Ø синусоида
3. Работа с таблицами
4. Анимация
5. Другие возможности
Возможности программы GeoGebra не ограничиваются созданием простых статичных учебных материалов. В программе предусмотрена возможность анимации чертежей. Первый способ применения анимации для создания заданий с автоматизированной проверкой — это создание тестов или тренажеров, в которых ограничено время на выполнение либо каждого отдельного задания, либо всего теста.
В то же время при использовании программы GeoGebra для создания заданий с автоматизированной проверкой возникает ряд сложностей:
• так как программа изначально не предназначалась для создания таких заданий, в ней отсутствуют готовые шаблоны, позволяющие быстро создать большое количество однотипных вопросов;
• для создания заданий с автоматизированной проверкой в программе GeoGebra учителю необходимо иметь хотя бы минимальные представления о математической логике и программировании;
• написание программы, осуществляющей проверку, требует довольно больших затрат времени
Рассмотрим пример применения данной программы на практическом занятии по геометрии в 8 классе.
Пример 1. Рассмотрим возможности использования ИГС на отдельных этапах работы с теоремой на примере утверждения: «Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия» (8 класс). Наиболее типичной ошибкой при изучении соотношении величин подобных треугольников для учащихся является проведение ложной аналогии «Если отношение соответственных сторон равно коэффициенту подобия, то это верно и для отношения площадей». Это заблуждение является настолько устойчивым, что единичный контрпример не позволяет убедить учащихся в необходимости отказаться от этой аналогии. В связи с этим работа с утверждением теоремы должна начинаться с накопления и обобщения фактов, альтернативных первичной гипотезе. Для накопления фактов можно использовать возможности ИГС, связанные с построением параметрически заданного динамического чертежа, а также использования функции записи данных в таблицу (рис. 1).

Рис.1
Пример 2.
Для объяснения построения окружности, вписанной в треугольник, можем также воспользоваться средой GeoGebra. Обозначив учебную проблему: «Как найти центр описанной окружности и ее радиус?» и обсудив ее, проведем построения в программе GeoGebra.
Итак, чтобы построить окружность, вписанную в треугольник, а заодно и добавить новую команду, выполним последовательность действий.
1. Построим треугольник.
2. Проведем биссектрисы его углов.
3. Отметим точку D пересечения биссектрис.
4. Спрячем биссектрисы, используя панель объектов.
5. Опустим перпендикуляр из точки пересечения биссектрис на одну из сторон треугольника. Отметим основание перпендикуляра Е и спрячем его, вновь используя панель объектов.
6. Построим окружность, проходящую через точки D и Е (О – ее центр, Е – точка на окружности).
7. Отметим точки касания окружности со сторонами треугольника.
8. Инструменты – Создать инструмент – Входные объекты (выбрать из списка или нажать на вершины треугольника) – Входные объекты (окружность и ее центр).
9. Имя и значок. Вписанная окружность. Описание: «Отметьте три вершины треугольника». Рисунок значка приготовить заранее.
10. Нажать на кнопку «Завершить». В окне появится новая команда, которой можно воспользоваться, если потребуется окружность, вписанная в  треугольник (рис.2).
треугольник (рис.2).
Рис. 2
Нетрудно убедиться, что чертеж опять получился динамичным. Для этого достаточно потянуть за одну из вершин фигуры. Форма и размеры треугольника изменятся, но окружность останется «привязанной» к треугольнику.
Подведём итог рассмотрения интерактивной геометрической среды GeoGebra 3D. Можно выделить ее «плюсы»:
· Полностью бесплатна;
· Полностью русифицирована;
· Легка в освоении;
· Работает на большинстве операционных систем;
· Простую интеграцию с офисными приложениями;
К недостаткам данной среды отнесем:
· Медлительность;
· Сложности при создании тестов и прочего.
Еще одной удобной программой для проведения практически занятий по геометрии, которую могут освоить учащиеся средней школы, является программа "Живая Математика".
Изучение материала по геометрии может быть следующим образом:
1) По готовым чертежам, разработанным учителем.
2) Самостоятельное моделирование учащимися геометрических объектов.
Данное программное средство обеспечивает высокое качество графических работ, что позволяет учащимся иметь высокую самооценку своей работы, по сравнению с традиционным подходом к изучению геометрии.
Живая математика представляет собой среду моделирования и динамического преобразования чертежей, графиков и других объектов; позволяет решать широкий круг задач при изучении геометрии, алгебры, тригонометрии и математического анализа.
Живая математика имеет полный набор возможностей для выполнения построений на плоскости, их преобразований и дальнейшей работы с ними, то есть практически полностью охватывает планиметрический материал. Предлагаемые создателями программы методические рекомендации это подтверждают — работе на плоскости посвящена большая часть предлагаемых материалов: от элементарных построений (точка, прямая, луч, отрезок, простейшие фигуры и пр.) до построения довольно сложных моделей, которые в той или иной степени можно использовать для наглядной демонстрации при доказательстве некоторых теорем из курса геометрии за 7–9 класс.
Что касается работы со стереочертежами, то возможности «Живой математики» довольно узки и специфичны. В среде отсутствует 3D-полотно, что, на первый взгляд, делает невозможными построение пространственных фигур и работу с ними. Тем не менее, построить объёмное тело (тело вращения и пр.), динамически изменяемое, всё-таки можно. Однако это построение будет довольно трудоёмким и времязатратным.
Приведем несколько примеров практических работ в среде «живая математика»
Пример 3.
Практическая работа "Внешний угол треугольника" позволяет наглядно продемонстрировать, как же изменяются градусная мера углов треугольника при изменении положения вершин (рис.3).

Рис.3
Пример 3.
В практической работе «Первый признак равенства треугольников» учащимся предлагается изменить масштаб треугольников и проследить за тем, как будут меняться его стороны и углы (рис. 4).
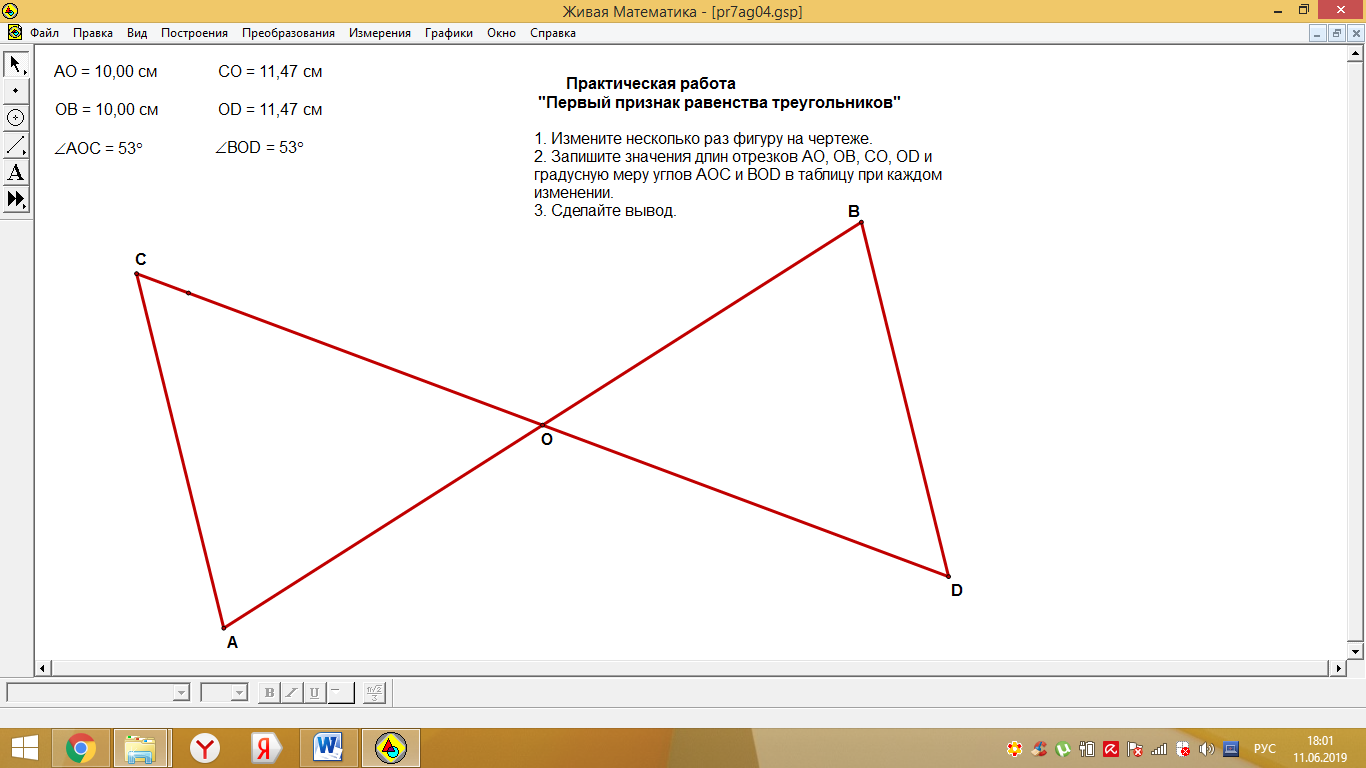
рис. 4
Пример 3.
Практическая работа «Медиана биисектрисса, высота треугольника» позволяет нагляно прослетить изменением длин медианы, биссекрисы и высоты при изменении формы треугльника (рис.5).

рис.5
Заключение
Практические занятия при изучении геометрии – это необходимый инструмент в руках учителя. Ведь он позволяет не только выполнять основные требования ФГОС, но и сделать уроки более интересными и разнообразными, что как следствие влечет за собой повышение учебной мотивации и заинтересованности учащихся.
В рассмотренных нами учебниках по геометрии, которые являются на сегодняшний день основными, практические работы и практические задания представлены в очень малом количестве. Поэтому современному учителю при подготовке и планировании уроков необходимо затрачивать больше времени на поиски и разработки методических пособий.
Практические работы могут быть представлены как в традиционном понимании, так и с использованием информационных технологий. Проведение практических работ в традиционном виде, по-моему, мнению наиболее актуально и полезно. При соблюдении принципа практико-ориентированности у учащихся не будет возникать вопрос «где пригодится геометрия», ведь на практических занятиях они будут применять полученные знания для решения «бытовых» задач. Проведение же практических работ с использованием интерактивных геометрических сред позволяет, реализовывать на уроке идеи исследовательского обучения, что также не маловажно.
Список используемой литературы
1. Аксютина, И. В. Формирование творческой деятельности учащихся при изучении систематического курса геометрии в основной школе / И. В. Аксютина // Образование, наука, культура в свете решения региональных проблем: сборник трудов II Международной конференции (Астрахань, 17–19 апреля 2008 г.). – Астрахань, 2008. – С. 50–53.
2. Белый, Б.Н. Измерительные работы на местности в связи с преподаванием математики: дис.. канд. пед. наук. – Киев, 1953.
3. Глейзер, Г.Д. Каким быть школьному курсу геометрии // Математика в школе. 1991. – № 4. – С. 68-71.
4. Зыкова, В.И. Формирование практических умений на уроках геометрии. – М.: Изд-во АПН РСФСР, 1963. – 200 с.
5. Федеральный закон от 29.12.2012 N 273-ФЗ «Об образовании в Российской Федерации (ред. от 25.11.2013; с изм. и доп., вступ. в силу с 01.01.2014) // Российская газета. – N 303. – 31.12.2012.
6. Тараник, В.И. Самостоятельная познавательная деятельность учащихся и ее развитие средствами практических работ по геометрии: учеб.-метод. пособие / В.И. Тараник / науч. ред. В.А. Далингер. – Омск: ООО «ИПЦ “Сфера”», 2009. – 184 с. (11,5 п.л.)
7. Практическая работа по геометрии 8 класс по теме Симметрия // infourok.ru URL: https://infourok.ru/prakticheskaya-rabota-po-geometrii-klass-po-teme-simmetriya-1488197.html (дата обращения: 11.06.19).
8. Практическая работа № 3 // gunkoiren.ucoz.ru URL: https://gunkoiren.ucoz.ru/_ld/1/121___3__21.doc (дата обращения: 10.06.19).
9. Практические работы 9 класс // pedportal.net URL: https://pedportal.net/starshie-klassy/geometriya/prakticheskie-raboty-9-klass-863487 (дата обращения: 11.06.19).