Проверочная работа «Действия над векторами в координатах»

Задания дистанционного обучения математике

Для студентов гр. МТП-1

План работы:

1. Перепишите теоретический материал в тетрадь

2. Перепишите образцы решения заданий в тетрадь

3. Выполните практическую работу № 21

4. Выполните на оценку по вариантам проверочную работу и отправьте её фото преподавателю 18.05.2020 до 14.00.

Тема: Решение задач с векторами в координатах

Теория:

Координаты точки

Три попарно перпендикулярные прямые с выбранными направлениями и единицей измерения образуют систему координат в пространстве. Точка пересечения всех прямых является началом системы координат.

 

 

Оси координат Ox, Oy и Oz называются соответственно: Ox — ось абсцисс, Oy — ось ординат, Oz — ось аппликат.

Через две пересекающиеся прямые можно провести плоскость. Получаем три координатные плоскости: (Oxy), (Oyz) и (Oxz).

 

 

Положение точки A в пространстве определяется тремя координатами: x, y и z.

 

 

Координата x называется абсциссой точки A, координата y — ординатой точки A, координата z — аппликатой точки A.

Записываются так: A(x;y;z).

Если точка находится на оси Ox, то её координаты X(x;0;0).

Если точка находится на оси Oy, то её координаты Y(0;y;0).

Если точка находится на оси Oz, то её координаты Z(0;0;z).

 

Если точка находится в плоскости Oxy, то её координаты A₁(x;y;0).

Если точка находится в плоскости Oyz, то её координаты A₂(0;y;z).

Если точка находится в плоскости Oxz, то её координаты A₃(x;0;z).

Координаты вектора

 

Если в системе координат от начальной точки отложить единичные векторы , то можно определить прямоугольный базис. Любой вектор можно разложить по единичным векторам и представить в виде Коэффициенты x, y и z определяются одним-единственным образом и называются координатами вектора.

Записываются так:

 

Рассмотрим правила о том, как с помощью координат записать:

Дано	Найти	Решение	Пример
	Сумму или разность векторов		, = =
	Умножение вектора на число
А(х1; у1; z1) В(х2; у2; z2)	Координаты вектора АВ	Из координат конца вычесть координаты начала	А(2; -3; 4), В(3; 1; 5). = =
А(х1; у1; z1) В(х2; у2; z2) С- середина АВ	Координаты середины отрезка	С	А(2; -3; 4), В(4; 1; 5). =(3; -1; 4,5).
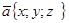
	Длину вектора
	Скалярное произведение векторов	Если , то	, = -3+(-8)+0 = - 11
	Угол между векторами	- угол острый - угол тупой - угол прямой	Смотри образцы

 

Образцы решения

Пример 1. Дано:А(-5; 7; 12), В(4; -8; 3), С(13; -23; -6). Лежат ли точки на одной прямой?

Решение: если векторы АВ и АС коллинеарные, то точки лежат на одной прямой.

Векторы коллинеарные, если их координаты пропорциональны. Найдём координаты векторов: ,

точки лежат на одной прямой.

Пример 2. Дан , А(0;1;-1), В(2;-3;2), С(4; 3;0). Найдите:

А) 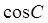и определите вид угла С (острый, тупой, прямой) Б) длину медианы АМ

В) Найдите на оси У координаты точки , чтобы .

Решение:

В А)

М

А В

. .

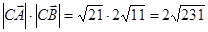угол С острый

Б) Так как АМ – медиана, то М – середина ВС,

,

В) Так как , то . Так как точка лежит на оси У, то D(0; у; 0).

,

.

2у – 4 = 0 у = 2. Значит D(0; 2; 0). Ответ: а) б) в) D(0; 2; 0).

Практическая работа № 21 «Решение задач с векторами в координатах»

1. Даны векторы: , , .

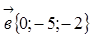Найдите: а) б) .

2. М – середина отрезка АВ, где А(0; 3; - 4), В (-2; 2; 0). Найдите координаты точки М.

3. М– середина отрезка АВ, где А(14; -8; 5), М (3; -2; -7). Найдите координаты точки В.

4. О – середина отрезка АВ, причем О лежит на оси абсцисс. Найдите m и n, если А(-3; m; 5), В(2; -2; n).

5. Дано: , А(5;-1;-2), В(1;5;0), С(2; 0;-1). СМ – медиана, МК – средняя линия треугольника. Найдите: а) длину медианы СМ б) длину МК.

6. Определите вид треугольника АВС (равнобедренный, равносторонний, прямоугольный), если А(-15; 0; 2), В(-12; 4; - 10). С (5; 12; 11).

7. Точка С является серединой отрезка АВ, причем точка А лежит в в плоскости ОУZ, а точка В – на оси Х. Найдите координаты концов отрезка и его длину, если С(6;2;3).

Проверочная работа «Действия над векторами в координатах»

1 вариант	2 вариант
Акулов К. Ю.	Арсланов И.И.
Бабиков Г.И.	Базуев В.Ю.
Булатов Е. Н.	Бухаров Д.В.
Глумов А.А.	Грошев М.Е.
Жуланов Н.А.	Карпов В.В.
Лобанов Н.А.	Малышев Д.В.
Нагаматуллин И.А.	Обухов В.Д.
Санников А.Н.	Стариков А.А.
Сутягин В.С.	Толмачев Р.В.
Трясцын К.Н.	Туманов А.Ю.
Чагин Н.В.	Шаравин Д.А.
Щеблёв М.А.	Юрков Д.И.
Долгих Н.В.	Сиразтдинов А.Р.
Чаплин М.В.	Белоногов А. В.
Юшков С.Ю.

Вариант 1.

Дан : А (2; -3; 4), В (1; 0; 2), С (1; 3; -2), СМ – медиана треугольника

Найдите: 1) 2 ) косинус угла С и его вид (острый, тупой или прямой)

Вариант 2.

Дан : А(1;0;2), В(0;-1;3), С(3;2;-2). ВМ – медиана.

Найдите: 1) , 2) 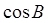и определите вид угла В (острый, тупой, прямой)