Порядок выполнения расчетного задания

Потеря устойчивости стержня, сжатого центральными силами

В упругой стадии деформирования величину критической сжимающей силы можно определить по формуле Эйлера:

где - коэффициент приведения длины, зависящий от способа закрепления концов стержня.

J_min- минимальный осевой момент инерции поперечного сечения стержня.

Формулой Эйлера можно пользоваться при условии .

где l - гибкость стержня,

где s_пц – предел пропорциональности материала.

Для стержней, у которых действительная гибкость меньше критической гибкости (), используют эмпирическую формулу Тетмайера – Ясинского для определения критических напряжений потери устойчивости:

s_кр .= а + в λ,

 

где а, в – эмпирические коэффициенты с размерностью напряжения. Для таких стержней

Р _кр= (а – в · λ) F _сеч.

 

При практических расчетах на устойчивость удобно пользоваться допускаемыми напряжениями сжатия при продольном изгибе

 

,

где j - коэффициент снижения основного допускаемого напряжения, изменяющийся в пределах 0 < j ≤ 1;

- основное допускаемое напряжение для материала стержня при сжатии.

Условие устойчивости записывается в виде:

.

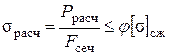Порядок выполнения расчетного задания

Для выполнения задания требуется:

1. Подобрать размеры поперечного сечения стержня с помощью таблиц коэффициентов снижения основного допускаемого напряжения методом последовательных приближений. В первом приближении принять

величину коэффициента снижения основного допускаемого напряжения

φ ₁= 0,5 в последующих приближениях принимать коэффициент φ как среднее арифметическое значение между принятым в предыдущем приближении и полученным табличным значением в этом же приближении.

2. Определить величину критической сжимающей силы Р _критич по формуле Эйлера или по формуле Тетмайера — Ясинского (в зависимости от величины гибкости стержня).

3. Определить величину коэффициента запаса устойчивости (n_уст).

Примечания:

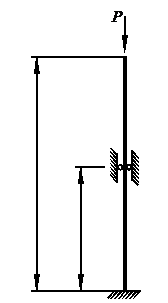
1. Схемы нагружения и закрепления стержней даны на стр. 46, 47 с величинами коэффициентов приведения длинны стержня v

2. Значения Величин Е, Р, l приведены в табл. 1 (варианты 1– 21.)

3. Виды поперечных сечений стержней приведены на стр. 49 – 54.

 

 

Таблица 1

 

Вариант 1

 

		0,1	0,2	0,3	0,4	0,5
v		1,87	1,73	1,60	1,47	1,35
	0,6	0,7	0,8	0,9	1,0
v	1,23	1,13	1,06	1,01	1,0

 

 

 

Вариант 2

 

 

		0,1	0,2	0,3	0,4	0,5
v		1,85	1,70	1,55	1,4	1,26
	0,6	0,7	0,8	0,9	1,0
v	1,11	0,975	0,852	0,757	0,699

 

Вариант 3

 

		0,1	0,2	0,3	0,4	0,5
v	0,5	0,467	0,436	0,412	0,41	0,439
	0,6	0,7	0,8	0,9	1,0
v	0,487	0,539	0,593	0,646	0,699

 

 

Окончание таблицы 1

Вариант 4

 

		0,1	0,2	0,3	0,4	0,5
v	0,5	0,463	0,426	0,391	0,362	0,350
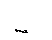
	0,6	0,7	0,8	0,9	1,0
v	0,362	0,391	0,426	0,463	0,5

 

 

Вариант 5

 

		0,1	0,2	0,3	0,4	0,5
v	0,699	0,652	0,604	0,558	0,518	0,5
	0,6	0,7	0,8	0,9	1,0
v	0,518	0,558	0,604	0,652	0,699

 

 

 

 

 

P

 

Вариант 6

 

		0,1	0,2	0,3	0,4	0,5
v	0,699	0,645	0,593	0,593	0,487	0,439
	0,6	0,7	0,8	0,9	1,0
v	0,41	0,412	0,436	0,467	0,5

 

Таблица 1

 

N ˚ - вар.	Р кн.	l м		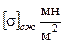Е
		4,2		2 · 10 5
		4,0		2,1 · 105
		3,8		2,2 · 10 5
		3,6		2 · 105
		3,4		1,9 · 105
		3,3		2 ·105
		3,2		2,1· 105
		3,1		2 ·105
		3,0	150.	2,2 · 105
		3,0		2 · 105
		2,9		l,9 · 105
		2,8		2 · 105
		2,7		2· 105
		2,6		1,95· 10 5
		2,5		2,05 · 105
		2,4		2,1 · 105
		2,4		2,15 · 105
		2,3		2,2 ·105
		2,3		2,0 · 105
		2,2		2,0 · 105
		2,1		2,0·105

 

 

Схемы поперечных сечений

 

 

 

 

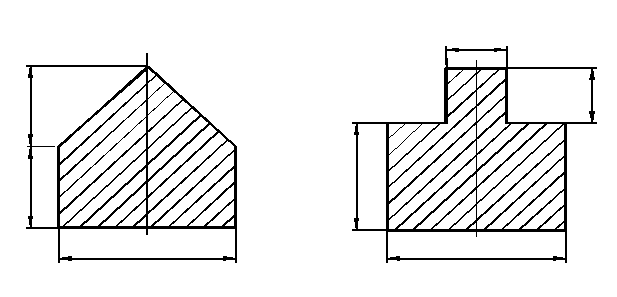
Продолжение таблицы 3

 

 

 

 

 

 

 

 

 

N˚- l ср.
l мм
t мм

 

 

N˚- l ср.
l мм
t мм

 

 

 

N˚- l ср.
l мм
t мм

N˚- l ср.
l мм
t мм

Пример 2.1. Расчет на устойчивость.

 

Подобрать размеры поперечного сечения стержня (рис.2.2) из расчета на устойчивость с помощью таблиц коэффициентов понижения основного допускаемого напряжения. Определить критическую силу по формулам Эйлера или по Тетмайера -Ясинского (в зависимости от Хгибкости).Определить коэффициент запаса устойчивости. Схемы закрепления стержня показаны на рис.2.1, вид поперечного сечения стержня – на рис.2.2.

 

Числовые данные:

Р =200 кН, l =3 м, Материал Ст 3 ГОСТ 380-88 ,

Е = 2 ∙10⁵ , υ = 0,7 – коэффициент приведения длины.

(Опорные условия одинаковые для обеих плоскостей конструкции).

Решение:

1.Определяем геометрические характеристики поперечного сечения стержня, выражая их через параметр а.

1.1.Определяем величину площади поперечного сечения стержня:

F _cеч.=3 а ² + а ² + 2 а ² = 6 а ².

1.2. Определяем положение центра тяжести поперечного сечения и положение главных центральных осей инерции сечения. Положение центра тяжести определяем в системе координатных осей у, х ₁ (рис. 2.2,)

Х _{1ц. т} = 0, т. к. ось у - ось симметрии.

где - статический момент поперечного сечения относительно оси X,

 

 

Главными центральными осями инерции поперечного сечения являются оси Y, X проходящие через центр тяжести сечения (рис. 2.2).

1.3. Определяем величины осевых моментов инерции поперечного сечения относительно главных центральных осей Y, X:

 

1.4. Определяем величину минимального радиуса инерции поперечного сечения

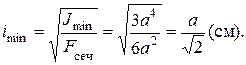
1.5. Определяем величину гибкости стержня λ:

2. Определяем размеры поперечного сечения стержня (размера) из расчета на устойчивость методом последовательных приближений.

2.1. Производим расчет в первом приближении. Принимаем величину

φ₁ = 0,5 (среднее значение, т.к. 0 < φ ≤1),

Принимаем а = 2,2 см. Гибкость стержня

Для материала Ст. 3 требуемая величина φ, определяемая по таблице = 0,38, что значительно отличается от принятой в первом приближении величины φ₁ = 0,5. Поэтому произведем расчет во втором приближении.
2.2. Расчет во втором приближении.

Принимаем то есть среднее арифметическое значение.

Принимаем а =2,37 см. Гибкость стержня

По таблице φ = f (λ) требуемая величина φ = 0,4136, что также еще значительно отличается от принятой во втором приближении величины φ₂ =0,44. Поэтому произведем расчет в тре­тьемприближении.

2.3. Расчет в третьем приближении.

Принимаем

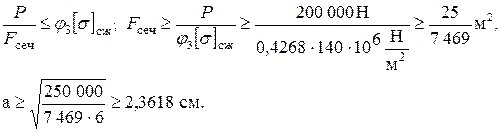
Принимаем a = 2,37 см. Гибкость стержня .

По таблице φ = f (λ) требуемая величина φ = 0,4246, что уже мало отличается от принятой в третьем приближении величины φ₃ = 0,4268. Производим расчет в последнем приближении.

2.4.Расчет в четвертом приближении

Принимаем ;

;

Принимаем а =2,37 см. Гибкость стержня

 

. По таблице φ = f (λ) требуемая величина φ=0,4246. Разница между принятым значением φ ₄ и требуемым (табличным) крайне не значительна

(менее 0,21%). Окончательно принимаем а = 2,37см (λ = 125,13). Проверим, выполняется ли условие устойчивости:

Условие устойчивости выполняется.

3. Определяем величину критической силы.

Для подобранного поперечного сечения (а = 2,37см) определяем величину критической сжимающей силы по формуле Эйлера т. к.

λ _действ > λ_кр для рассматриваемого материала (Ст. 3). λ _действ= 125,13,

λ_кр =100

 

4. Определяем величину коэффициента запаса устойчивости.

Пример 2.2. Расчет на устойчивость

Подобрать размеры составного поперечного сечения, показанного на рис.2.4, номер двухтаврового профиля взять по ГОСТ 8239-84.Схема закрепления стержня показана на рис.2.3.Определить коэффициент запаса устойчивости.

 

 

 

 

 

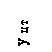Числовые данные:

 

Р = 380 кH, l = 5 м, Материал Ст 3 по ГОСТ 380-88 =140

 

v =1 – коэффициент приведения длинны. Опорные устройства одинаковы для обеих плоскостей конструкции.

Требуется. 1. Подобрать размеры поперечного сечения (номер двутаврового профиля по ГОСТ 8239 – 84 рис.2.4.) из расчета на устойчивость с помощью таблицы коэффициентов φ = f (λ).

2. Определить коэффициент запаса устойчивости.

Решение:

1.Определяем размеры поперечного сечения стержня (номер двутаврового профиля по ГОСТ 8239-89) из расчета на устойчивость методом последовательных приближений.
1.1. Произведем расчет в первом приближении. Принимаем φ₁=0,5 (среднее значение, т.к. 0 < φ ≤1)

.

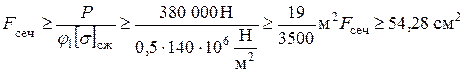По таблице ГОСТ 8239 – 89 выбираем номер профиля 20 а. Размер профиля и геометрические характеристики профиля 20 а выписываем из таблицы ГОСТ 8239 – 89 (рис.2.5): h = 20 см, b = 11см, F _проф.=28,9 см² (площадь поперечного сечения профиля), J_х = 2030 см⁴, J _у= 155 см⁴, d = 5,2 мм.

Определяем положение центра тяжести поперечного сечения в системе координат Y,X ₁, X _1ц.м.= 0 (ось Y – ось симметрии),

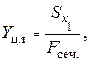
где S _{х 1} – статический момент сечения относительно оси Х ₁ (ось Х ₁ проходит через центр тяжести нижнего профиля см. рис. 2.4).

 

Главными центральными осями инерции поперечного сечения являются оси Y, X, относительно которых,

Рис.2.5.

определяем осевые моменты инерции поперечного сечения

Рис.2.5

(рис.2. 4) 155 + 2 030 = 2 185 см⁴,

J_х = 2 030 + 28,9(5,13) + 155 + 28,9(5,13) = 3 706,12;

J _min = J_у = 2 185 см⁴. Минимальный радиус инерции поперечного сечения

. Гибкость стержня.

По таблице φ=f(λ) требуемая величина φ для гибкости λ_min=81,3 составляет φ=0,742. Это значение φ значительно отличается от принятой в первом приближении величины

φ₁= 0,5, поэтому производим расчет во втором приближении.

1.2. Расчет во втором приближении.

Принимаем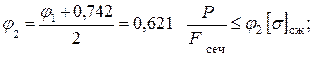

По таблице ГОСТ 8239 – 89 выбираем номер профиля 18. Размеры и геометрические характеристики профиля 18 вписываем из таблицы ГОСТ 8239 – 89 (рис.2.5): h = 18 cм, b = 9 cм, F _проф. = 23,4 см², J_x = 1 290 см⁴, J_y = 82,6 см⁴ , d =0,51. Определяем положение центра тяжести поперечного сечения в системе координат Y, X₁, (рис. 2.5.). X _1ц.т=0,

Определяем осевые моменты инерции поперечного сечения относительно главных центральных осей Y, X: J_у = 82,6 + 1 290 = 1372,6 см⁴;

J_x =1290 см ⁴ + 23,4 см ², (4,6275 см)² + 82,6 см⁴ + 23,4 см²· (4,6275 см)² = =2374,12 см⁴. J _min= J _у = 1 372,6 см⁴. Минимальный радиус инерции поперечного сечения . Гибкость стержня 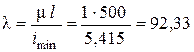. По таблице φ = f(x) требуемая величина φ =0,669 (для Ст.3 и λ_min=92,33), что значительно отличается от принятой в втором приближении величины φ₂ = 0,621. Поэтому производим расчет в третьем приближении.

 

1.3. Расчет в третьем приближении.

Принимаем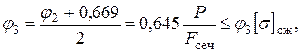

 

По таблице ГОСТ 8239 – 89 выбираем профиль 18, размеры и геометрические характеристики которого, приведены в расчете второго приближения данного примера. Требуемая величина φ =0,669 (для Ст. 3 и λ_min = 92,33) мало отличается от принятой в третьем приближении величины φ₃ = 0,645.Если произвести расчет в четвертом приближении, то опять получим тот же результат (номер профиля 18 по ГОСТ 8239-89). Поэтому окончательно выбираем профиль 18.

Проверим, выполняется ли условие устойчивости: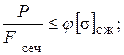

81,196 < 93,66 , условие устойчивости выполняется.
2. Определяем величину критической силы.

 

Для подобранного поперечного сечения стержня (двутавровые профили номер 18) определяем величину критической сжимающей силы по формуле Ф. Ясинского, т. к, λ _{действ.}< λ _кр для рассматриваемого материала (Ст. 3) λ _{действ.}= 92,33, λ _кр.≈ 100. σ_крит.= а – b λ – формула Тетмайера - Ясинского - для Ст.3)

3. Определяем величину коэффициента запаса устойчивости

2.4. Проектировочный расчет без последовательных приближений.

 

Условие прочности 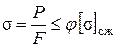, делим его на и подставляем в левую часть , преобразуем его к виду* где

Коэффициент R₀ , для сечений из не прокатных профилей зависит только от формы поперечного сечения, а значения коэффициента с легко получить через λ и φ. Приведем выражения коэффициента R₀для некоторых форм поперечного сечения.

 

	Рис. 2.5

 

Дополним стандартную таблицу коэффициента φ коэффициентом с табл.4

Таблица 4

 

Значения коэффициентов φ и с
λ	Ст. 2, Ст. 3, Ст. 4	Ст. 5	15ХЕ HD	Д16Т	Ч4 12-28 Ч4 21-40
Ф	С · 10 - 3	φ	С · 10 - 3	φ	С · 10 - 3	φ	С · 10 - 3	φ	С · 10 - 3
	1,00	0,00	1,00	0,00	1,00	0,00	1,00	0,00	1,00	0,00
	0,99	0,10	0,98	0,10	0,98	0,10	1,00	0,10	0,96	0,10
	0,97	0,41	0,95	0,42	0,95	0,42	1,00	0,40	0,91	0,44
	0,95	0,95	0,92	0,98	0,93	0,97	0,84	1,07	0,81	1,11
	0,92	1,74	0,89	1,82	0,90	1,78	0,70	2,28	0,69	2,32
	0,89	2,81	0,86	2,91	0,83	3,01	0,57	4,39	0,57	4,39
	0,86	4,19	0,82	4,39	0,78	4,62	0,46	7,8	0,44	8,18
	0,81	6,05	0,76	6,45	0,71	6,91	0,35	14,0	0,34	14,4
	0,75	8,53	0,70	9,14	0,63	10,2	0,27	23,7	0,26	24,6
	0,69	11,7	0,62		0,54	15,0	0,21	38,6	0,20	40,5
	0,60	16,7	0,51	19,6	0,45	22,2	0,17	58,8	0,16	62,5
	0,52	23,3	0,43	28,1	0,39	31,0	0,14	86,4
	0,45	32,0	0,38	37,9	0,33	43,6	0,12
	0,40	42,3	0,32	52,8	0,29	59,2	0,10
	0,36	54,4	0,28	70,0	0,26	75,3	0,087
	0,32	70,3	0,26	86,5	0,23	97,8	0,075
	0,29	88,3	0,24		0,21
	0,26		0,21		0,19
	0,23		0,19		0,17
	0,21		0,17		0,15
	0,19		0,16		0,13

 

Пример 3: Требуется определить диаметр D для стержня изображенного на рис. 2.6.

 

 

Е =2·10⁵ МПа, =120 МПа. Значение коэффициента v выбираем из таблицы 1, v =0,439. Значения геометрических характеристик для данного поперечного сечения:

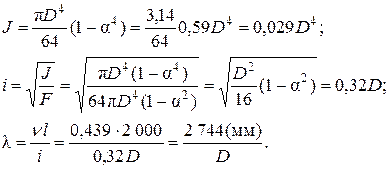
В начале решим задачу методом последовательных приближений 1.Первое приближение φ₁ = 0,5,

 

2. Второе приближение

3. Третье приближение

Расхождение с предыдущим решением , по рекомендациям в некоторых учебниках этого вполне достаточно, диаметр D ₃ можно считать окончательным.

 

Решим задачу по преобразованному условию прочности

Получилось решение, к которому мы стремились при последовательных приближениях (76,67→ 64,05→ 60,1→57,23). Назовем это решение точным.

Исследуем сколько еще нужно приближений чтобы получить это решение методом последовательных приближений.

4.Четвертое приближение

5.Пятое приближение

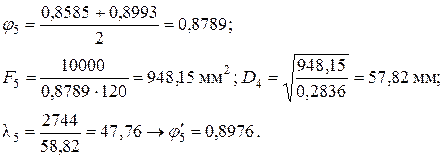
6. Шестое приближение

Это решение уже почти совпадает с точным, хотя видно, что приближение стало уже медленным. Изобразим это графически на рис.2.7.

 

 

 

 

Из рисунка видно, что быстро сходящимся процесс является только на первых приближениях.

Сопоставим подученные решения по напряжениям. Напряжение точного решения . В шестом приближении Расхождение с точным решением

.

В пятом приближении

расхождение между пятым и шестым

В четвертом приближении

 

расхождение между четвертым и пятым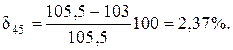

В третьем приближении

расхождение между третьим и четвертым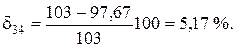

Отсюда видно, что на третьем приближении останавливаться нельзя. Сопоставлять приближения нужно не по коэффициенту φ, а по

напряжениям и то рекомендовать расхождение между последними приближениями не более 3%. И главное – объем вычислений при решении по преобразованному условию прочности в несколько раз меньше, чем методом последовательных приближений (до сих пор рекомендуемым в учебной литературе).Конечно нужно иметь выражение коэффициента R₀ для соответствующих профилей. Для сечений из прокатных профилей решение с помощью преобразованного условия прочности получается со второго приближения, так как для них не соблюдено подобие в размерах.

 

 

Контрольные вопросы

1)Что такое «устойчивость»?

2) Дать определение критической силы

3) Oт чего зависит величина гибкости конкретного стержня?

4) От чего зависит величина предельной гибкости?

5) В каких случаях величина критической силы определяется по формуле Эйлера, а в каких – по формуле – Тетмайера – Ясинского.

6)В сторону какой оси сечения изогнется стержень при потере устойчивости, если имеем следующий поперечные сечения.

Y

X

X

X

X

Y