Зависимости для определения необходимого объема выборки для некоторых способов формирования выборочной совокупности приведены в таблице.
Таблица __ - Необходимый объем выборки для некоторых способов формирования выборочной совокупности
| Вид выборочного наблюдения | Повторный отбор | Бесповторный отбор |
| Собственно - случайная выборка: а) при определении среднего размера признака б) при определении доли признака Механическая выборка | 
 то же
то же
| 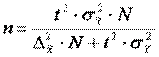
 то же
то же
|
Рассмотрим ряд примеров использования приведенных в табл.___ зависимостей.
Пример №1. В микрорайоне проживет 5000 семей. В порядке случайной бесповторной выборки определить необходимый объем выборки при определении среднего размера семьи при условии, что ошибка выборочной средней не должна превышать 0,8 человека с вероятностью Р = 0,954 и при среднеквадратическом отклонении 3,0 человека.
Так как, при Р = 0,954 Þ t -2, то необходимая численность выборки равна
n = (22*32*5000)/ (5000*0, 64+22 *32)»56 семей
Пример №2. Для определения средней длины детали следует провести обследование методом случайного повторного отбора. Какое количество деталей необходимо отобрать, чтобы ошибка выборки не превышала 3 мм с вероятностью 0,997 при среднем квадратическом отклонении 6 мм.
При Р = 0,997 Þ t = 3. Тогда
n = (32 * 62)/ 32 = 36 деталей
Понятие о малой выборки
При большом числе единиц выборочной совокупности (n >100) распределение случайных ошибок выборочной средней в соответствии с теоремой А.М. Ляпунова нормально или приближается к нормальному по мере увеличения числа наблюдений.
Однако в практике статистического исследования в условиях рыночной экономики все чаще приходится сталкиваться с малыми выборками.
Малой выборкой называется такое выборочное наблюдение, численность единиц которого не превышает 30. Разработка теории малой выборки была начата английским статистиком В.С. ГОССЕТОМ (печатавшимся под псевдонимом СТЬЮДЕНТ). Он доказал, что оценка расхождения между средней малой выборки и генеральной средней имеет особый закон распределения.
При оценке результатов малой выборки величина генеральной совокупности не используется. Для определения возможных пределов ошибки пользуются критерием Стьюдента, определяемым по формуле
 , ()
, ()
где  - средняя ошибка малой выборки
- средняя ошибка малой выборки
Для малой выборки величина коэффициента доверия t по другому связана с вероятностной оценкой, чем при большой выборке (так как, закон распределения отличается от нормального).
Согласно установленному Стьюдентом закону распределения, вероятная ошибка распределения зависит как от величины коэффициента доверия t, так и от объема выборки. В таблице ___ приведен фрагмент таблицы распределения Стьюдента.
Таблица__ - Распределение вероятностей в малых выборках в зависимости от коэффициента доверия t и объема выборки
| n/t | ? | |||||||||
| 0,5 1.0 1,5 2,0 2,5 3,0 | 348 608 770 860 933 942 | 356 626 792 884 946 960 | 362 636 806 908 955 970 | 366 644 816 908 959 976 | 368 650 832 914 963 980 | 370 654 828 920 966 938 | 372 656 832 924 968 984 | 376 666 846 932 975 992 | 378 670 850 940 978 992 | 383 683 865 954 988 977 |
| Примечание. 1. Для определения вероятности соответствующие табличные значения необходимо разделить на 1000. |