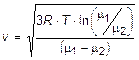Функция распределения давления в изотермической атмосфере в однородном гравитационном поле - барометрическая формула:
,
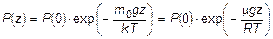z – координата точки наблюдения, отсчитываемая по координатной вертикальной оси, направленной вверх.
Функция распределения концентрации газа в приближении изотермичности газа и однородности гравитационного поля:
.
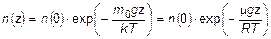Л.Больцман показал, что для газа одинаковых частиц в любом внешнем потенциальном силовом поле справедлива функция распределения концентрации частиц по потенциальным энергиям:
.
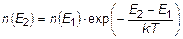Здесь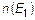 
- концентрация частиц в области, где энергия взаимодействия каждой из них с внешним полем равна 
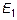. Аналогично трактуется концентрация 
.
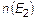10.1. Вычислите давление воздуха на дне скважины глубиной 8 км, если молярная масса воздуха 29 кг/кмоль, универсальная газовая постоянная 8,31 Дж/(моль К), давление у поверхности Земли 101,3 кПа, температура по всей глубине одинакова и равна 270 C.
10.2. Обсерватория расположена на высоте 3250 м над уровнем моря. Вычислите величину давления воздуха на этой высоте при условии, что температура воздуха внизу и наверху одинакова и равна 50 С. Молярная масса воздуха 29 кг/кмоль, универсальная газовая постоянная 8,31 Дж/(моль К), давление на уровне моря 101,3 кПа.
10.3 Найдите высоту над поверхностью Земли, на которой атмосферное давление в два раза меньше, чем на поверхности. Температура 280 К, молярная масса воздуха 29 кг/кмоль, универсальная газовая постоянная 8,31 Дж/(моль К), ln 2 = 0,69.
10.4. Найдите, на какой высоте над поверхностью Земли атмосферное давление в три раза меньше, чем на ее поверхности. Температура 290 К, молярная масса воздуха 29 кг/кмоль, универсальная газовая постоянная 8,31 Дж/(моль К), ln 3 = 1,099.
|
|
10.5. Найдите разность высот, на которых плотности воздуха при температуре 00 C отличаются в 2,7 раз. Молярная масса воздуха 29 кг/кмоль, универсальная газовая постоянная 8,31 Дж/(моль К).
10.6. Пусть a 0 – отношение концентрации молекул водорода к концентрации молекул азота вблизи поверхности Земли, а a – соответствующее отношение на высоте 3 км. Вычислите отношение a / a 0.Температура 280 К, молярная масса водорода 2 кг/кмоль, азота 28 кг/кмоль, универсальная газовая постоянная 8,31 Дж/(моль К).
10.7. Барометр в кабине летящего самолета все время показывает одинаковое давление 79 кПа, благодаря чему летчик считает высоту полета неизменной. Однако, температура воздуха за бортом самолета изменилась с 50 С до 10 С. На сколько ошибся летчик в определении высоты? Молярная масса воздуха 29 кг/кмоль, универсальная газовая постоянная 8,31 Дж/(моль К), давление у поверхности Земли 101,3 кПа.
10.8. Пылинки массой 10-21 кг взвешены в воздухе. Температура воздуха 300 К, постоянная Больцмана 1,38∙10-23 Дж/К. Вычислите толщину слоя воздуха, в пределах которого концентрация пылинок различается не более, чем на 1%.
10.9. Перрен, наблюдая при помощи микроскопа изменение концентрации взвешенных частиц гуммигута с изменением высоты и применяя барометрическую формулу, экспериментально нашел значение постоянной Авогадро. Оказалось, что при расстоянии между двумя слоями 100 мкм, число взвешенных частиц гуммигута в одном слое вдвое больше, чем в другом. Частицы гуммигута находятсяво взвешенном состоянии в жидкости, плотность которой на 200 кг/м3 меньше плотности частиц. Температура жидкости 200 С, диаметр частицы 0,3 мкм, универсальная газовая постоянная 8,31 Дж/(моль К). Вычислите значение постоянной Авогадро.
|
|
10.10. Закрытую с обоих торцов горизонтальную трубку длины 1 м перемещают с постоянным ускорением, направленным вдоль ее оси. Внутри трубки находится аргон при температуре 330 К. Вычислите ускорение трубки, при котором концентрации аргона вблизи торцов трубки будут отличаться друг от друга на 1%. Молярная масса аргона 40 кг/кмоль, универсальная газовая постоянная 8,31 Дж/(моль К).
10.11. Закрытую с обоих торцов горизонтальную трубку длины 1 м вращают с постоянной угловой скоростью вокруг вертикальной оси, проходящей через один из ее торцов. Внутри трубки находится углекислый газ при температуре 300 К. Вычислите угловую скорость трубки, при которой отношение концентраций молекул вблизи торцов трубки будет равно 2,7. Молярная масса углекислого газа 44 кг/кмоль, универсальная газовая постоянная 8,31 Дж/(моль К).
Основное соотношение, определяющее смысл одномерной функции распределения Максвелла по проекциям скорости молекул на произвольную координатную ось Z:
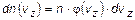
- количество молекул в единице объема, у которых проекция скорости лежит в диапазоне от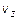 
до 
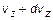пропорционально полному количеству молекул в единице объема, пропорционально ширине диапазона скоростей 
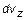и зависит от самой величины : 
.
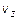Вероятность события, состоящего в том, что скорость произвольной молекулы лежит в диапазоне от 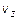до 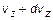, равна 
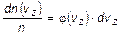. Поэтому условие нормировки функции 
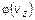принимает вид: 
.
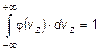Основное соотношение, определяющее смысл функции распределения Максвелла по модулям скорости молекул:
|
|
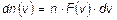
- количество молекул в единице объема, у которых модуль скорости лежит в диапазоне от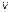 
до 
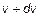пропорционально полному количеству молекул в единице объема, пропорционально ширине диапазона скоростей 
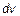и зависит от самой величины :
.
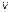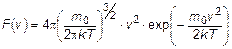Вероятность события, состоящего в том, что скорость произвольной молекулы лежит в диапазоне от 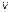до 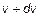, равна 
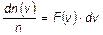. Поэтому условие нормировки функции 
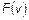принимает вид: 
.
Формулы для вычисления наиболее вероятной, средней арифметической и средней квадратичной скорости:
,
,
.
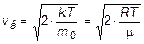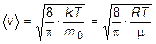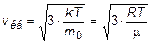10.12. Газообразный азот находится в сосуде при температуре 300 К. Вычислите отношение числа молекул с компонентами скорости вдоль оси Z в интервале от 300 м/с до 303 м/с к числу молекул с компонентами скорости вдоль оси Z в интервале от 500 м/с до 505 м/с. Молярная масса азота 28 кг/кмоль, универсальная газовая постоянная 8,31 Дж/(моль К).
10.13. Газообразный азот находится в сосуде при температуре 300 К. Вычислите вероятность того, что молекула азота имеет скорость с компонентами вдоль осей X, Y, Z в интервалах от 300 м/с до 303 м/с, от 400 м/с до 404 м/с и от 500 м/с до 505 м/с соответственно. Молярная масса азота 28 кг/кмоль, универсальная газовая постоянная 8,31 Дж/(моль К).
10.14. Найдите с помощью функции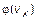 
число b молекул газа, падающих в единицу времени на единичную площадку, перпендикулярную координатной оси X, если концентрация молекул n, температура газа T и масса каждой молекулы m 0. Искомую величину выразите через среднюю скорость 
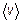молекулы. Возникающий при вычислении интеграл 
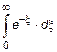равен единице.
10.15. Найдите с помощью функции 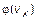давление газа на стенку сосуда, если температура газа T и концентрация молекул n. Возникающий при вычислении интеграл 
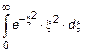равен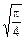 
.
10.16. Вычислите температуру кислорода, для которого функция распределения по скоростям имеет максимум при скорости 420 м/с. Молярная масса кислорода 32 кг/кмоль, универсальная газовая постоянная 8,31 Дж/(моль К).
10.17. Найдите количество молекул кислорода, содержащегося в сосуде объемом 100 см3 при давлении 104 Па, если их средняя скорость 400 м/с. Молярная масса кислорода 32 кг/кмоль,постоянная Авогадро 6∙1023 1/моль.
10.18. Некоторый газ массы 0,6 г в сосуде объемом 4 л создает давление 200 кПа. Вычислите среднюю квадратичную скорость молекул газа.
10.19. Вычислите температуру газа, состоящего из смеси азота и кислорода, при которой наиболее вероятные скорости молекул азота и кислорода будут отличаться друг от друга на 30 м/с. Молярная масса азота 28 кг/кмоль, кислорода 32 кг/кмоль, универсальная газовая постоянная 8,31 Дж/(моль К).
10.20. Вычислите относительное число молекул газа, скорости которых отличаются не более, чем на 1% от значения средней квадратичной скорости.
10.21. Вычислите относительное число молекул газа, скорости которых отличаются не более, чем на 1% от значения наиболее вероятной скорости.
10.22. Вычислите относительное число молекул азота при температуре 1700С, которые обладают скоростями от 295 м/с до 305 м/с. Молярная масса азота 28 кг/кмоль, универсальная газовая постоянная 8,31 Дж/(моль К).
10.23. Найдите скорость, при которой для некоторого идеального газа при температурах T 1 и T 2, совпадают плотности вероятности распределения молекул по абсолютным величинам скоростей. Молярная масса газа μ.
10.24. Найдите скорость, при которой для двух идеальных газов с молярными массами μ1 и μ2 при одной и той же температуре T совпадают плотности вероятности распределения молекул по абсолютным величинам скоростей.
ОТВЕТЫ
10.1. 2,6∙105 Па
10.2. ≈ 67 кПа
10.3. 5,5 км
10.4. 9,1 км
10.5. 7.8 км
10.6. 1,4
10.7. 28 м
10.8. 4,1 мм
10.9. 5,9∙1023 1/моль
10.10. 686 м/с2 ≈ 70∙g
10.11. 337 рад/с
10.12. 1,5
10.13. 9∙10-9
10.14. 
10.15.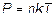 
10.16. 340 К
10.17. 3∙1020
10.18. 2∙103 м/с
10.19. 337 К
10.20. 1,85%
10.21. 1,66%
10.22. 0,011
10.23.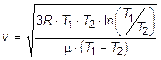 
10.24. 