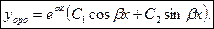Метод вариации произвольных постоянных для линейного неоднородного ДУ
С перем. коэфф. (для ДУ 2-го порядка)
Этот метод рассмотрим на примере уравнения II порядка:
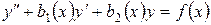 . .
| (1) |
Запишем однородное уравнение, соответствующее уравнению (1):
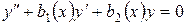 . .
| (5) |
Пусть 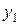 и
и 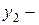 фундаментальная система решений уравнения (2), тогда его общее решение
фундаментальная система решений уравнения (2), тогда его общее решение 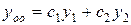 .
.
Решение уравнения (1) будем искать так: в 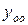 варьируем произвольные постоянные, т.е. будем считать их функциями от х, т.е.
варьируем произвольные постоянные, т.е. будем считать их функциями от х, т.е. 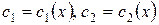 .
.
И потребуем, чтобы функция 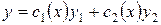 удовлетворяла уравнению (1).
удовлетворяла уравнению (1).
Вычислим производную:
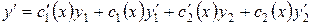 .
.
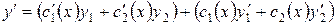 .
.
Потребуем, чтобы выполнилось равенство:
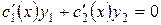 . .
| (А) |
Тогда 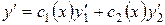 , следовательно,
, следовательно,
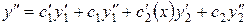 .
.
Подставляя 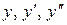 в уравнение (1), получим тождество:
в уравнение (1), получим тождество:
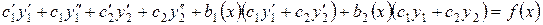 .
.
Сгруппируем слагаемые с 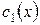 и
и  :
:
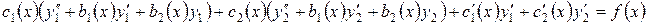
Обе скобки равны нулю, так как 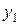 и
и 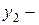 решения уравнения (2).
решения уравнения (2).
Значит, остается:
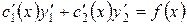 . .
| (В) |
Таким образом, чтобы функция 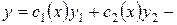 была решением уравнения (1) достаточно, чтобы выполнялись равенства (А) и (В), т.е. приходим к системе:
была решением уравнения (1) достаточно, чтобы выполнялись равенства (А) и (В), т.е. приходим к системе:
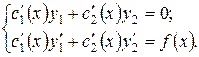
| (С) |
Функции 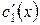 и
и 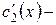 неизвестные в этой системе. Определитель этой системы – есть вронскиан решений
неизвестные в этой системе. Определитель этой системы – есть вронскиан решений 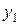 и
и 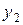 в силу фундаментальности решений
в силу фундаментальности решений 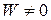 , значит, система имеет единственное решение:
, значит, система имеет единственное решение:
 .
.
Интегрируя, находим:
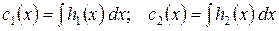 .
.
Подставляя найденные функции в общий вид решения, получаем общее решение линейного неоднородного уравнения:
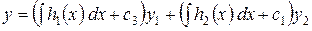 .
.
Линейные однородные ДУ с постоян. Коэффициентами
Линейным дифференциальным уравнением второго порядка называется уравнение вида:
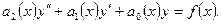
Если 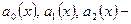 постоянные числа, то уравнение будем называть уравнением с постоянными коэффициентами. Кроме этого, будем считать что коэффициент при второй производной равен 1. Положим
постоянные числа, то уравнение будем называть уравнением с постоянными коэффициентами. Кроме этого, будем считать что коэффициент при второй производной равен 1. Положим 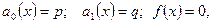 где
где 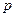 и
и  произвольные числа.
произвольные числа.
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами (ЛОДУ) называется уравнение вида
|
|
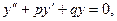
где 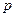 и
и  некоторые действительные числа.
некоторые действительные числа.
Общее решение ЛОДУ находится достаточно просто, если известны, так называемые, линейно независимые частные решения этого уравнения.
Функции 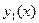 и
и 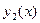 называются линейно независимыми на множестве D, если их отношение не является постоянной величиной, то есть
называются линейно независимыми на множестве D, если их отношение не является постоянной величиной, то есть 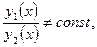 или другими словами: не существует такого постоянного числа
или другими словами: не существует такого постоянного числа 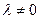 при котором выполнено равенство
при котором выполнено равенство 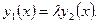
В противном случае, функции 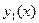 и
и 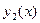 называются линейно зависимыми. Например, функции
называются линейно зависимыми. Например, функции 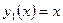 и
и 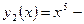 линейно независимые, а функции
линейно независимые, а функции 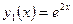 и
и 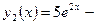 линейно зависимые.
линейно зависимые.
Обозначим через 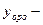 общее решение однородного уравнения ().
общее решение однородного уравнения ().
Теорема 8.4. (о структуре общего решения ЛОДУ второго порядка). Если 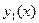 и
и 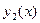 – два линейно независимые частные решения ЛОДУ
– два линейно независимые частные решения ЛОДУ 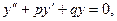 то функция
то функция 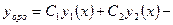 общее решение этого уравнения, где
общее решение этого уравнения, где 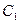 и
и 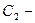 произвольные постоянные.
произвольные постоянные.
Замечание: Не существует общего метода нахождения частных решений уравнения 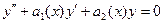 , когда коэффициент
, когда коэффициент 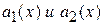 переменные, но для случая, когда они являются константами, Эйлером создан очень удобный метод нахождения частных решений.
переменные, но для случая, когда они являются константами, Эйлером создан очень удобный метод нахождения частных решений.
Характеристические уравнения для ЛОДУ второго порядка:
Будем искать решение 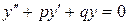 в виде
в виде 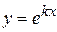 , где k-const.
, где k-const.
Очевидно, что 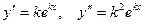 . Подставим эти выражения в уравнение:
. Подставим эти выражения в уравнение:
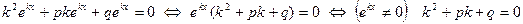
Уравнение 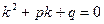 называется характеристическим уравнением дифференциального уравнения
называется характеристическим уравнением дифференциального уравнения 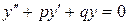 .
.
Характеристическое уравнение 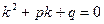 есть алгебраическое квадратное уравнение, имеющее два корня
есть алгебраическое квадратное уравнение, имеющее два корня 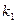 и
и 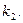 Эти корни, в зависимости от дискриминанта, могут быть действительными и не равными друг другу, действительными и равными и комплексно-сопряженными.
Эти корни, в зависимости от дискриминанта, могут быть действительными и не равными друг другу, действительными и равными и комплексно-сопряженными.
|
|
1. 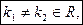 т.е корни действительные и не равные друг другу.
т.е корни действительные и не равные друг другу.
По теореме общее решение ЛОДУ второго порядка имеет вид:
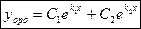
2. 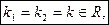 т.е корни действительные и равные друг другу.
т.е корни действительные и равные друг другу.
По теореме общее решение ЛОДУ второго порядка имеет вид:
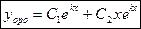 или
или 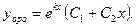
3. 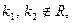 т.е корни комплексно сопряженные числа:
т.е корни комплексно сопряженные числа: 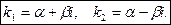
По теореме общее решение ЛОДУ второго порядка имеет вид:
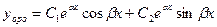 или
или