Г. 10 класс. Теория.
Алгебра и начала математического анализа, 10 класс.
Учитель Трипольская М.В.
Урок №15. Действительные числа.
Перечень вопросов, рассматриваемых в теме
1) множество иррациональных чисел;
2) множество рациональных чисел;
3) правила выполнения действий с бесконечными десятичными дробями;
4)определение бесконечно убывающей геометрической прогрессии.
Глоссарий по теме
Рациональные числа – это такие числа, которые можно записать в виде обыкновенной дроби 
, где m — целое число, n — натуральное число, обозначаются буквой Q.
Иррациональные числа - это действительные числа, которые нельзя представить в виде обыкновенной дроби. Иррациональное число может быть представлено в виде бесконечной непериодической дроби, т.е. числа после запятой в записи данного числа не повторяются.
Дробные числа – это числа, которые можно записать в виде обыкновенной дроби.
Все основные действия над рациональными числами сохраняются и для действительных чисел (переместительный, сочетательный и распределительный законы, правила сравнения, правила раскрытия скобок и т.д.).
Арифметические операции над действительными числами обычно заменяются операциями над их приближениями.
Геометрическая прогрессия называется бесконечно убывающей, если модуль её знаменателя меньше единицы.
Теоретический материал для самостоятельного изучения
Все числа, которые мы изучаем в школе, называются действительными числами. Они образуют множество действительных чисел, которые принято обозначать латинской буквой R.
В свою очередь все действительные числа можно разделить на 2 группы: рациональные числа и иррациональные числа.
|
|
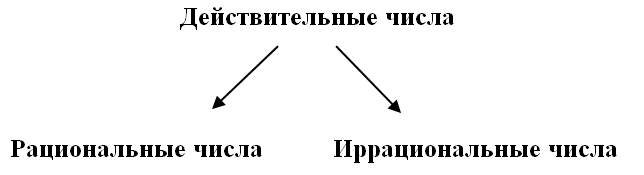
Рациональные числа – это такие числа, которые можно записать в виде обыкновенной дроби , где m —целое число, n — натуральное число, обозначаются буквой Q.
Пример: -3; -0,5; 
.
Иррациональные числа - это действительные числа, которые нельзя представить в виде обыкновенной дроби. Иррациональное число может быть представлено в виде бесконечной непериодической дроби, т.е. числа после запятой в записи данного числа не повторяются.
Пример: π=3,141592…; 0, 113456....
Рациональные числа, в свою очередь, можно разделить на 2 вида – это целые числа и дробные числа.
Дробные числа – это числа, которые можно записать в виде обыкновенной дроби.
Целые же числа можно разделить еще на несколько групп: отрицательные целые числа, нуль и положительные (натуральные) целые числа.
На числовой оси (Ох) между целыми числами будут находиться дробные иррациональные числа. Все вместе они будут представлять собой множество действительных чисел, R.
Обратите внимание, что все основные действия над рациональными числами сохраняются и для действительных чисел (переместительный, сочетательный и распределительный законы, правила сравнения, правила раскрытия скобок и т.д.).
Арифметические операции над действительными числами обычно заменяются операциями над их приближениями.
Числа 4; 4,2; 4,28 и т.д. являются последовательными приближениями значений суммы
.
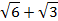Пусть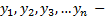 
это последовательные приближения действительного числа у с точностью до 1, до 0,1, до 0,01 и т.д. Тогда погрешность приближения 
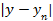как угодно близко приближается к нулю.
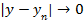при 
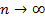или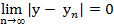 
|
|
Читается «модуль разности у и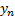 
стремится к нулю при n, стремящемся к бесконечности» или «предел модуля разности у и 
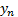при n, стремящемся к бесконечности, равен нулю»
Т.е. если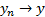 
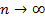при или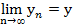 
Модуль действительного числа у обозначается как |у| и определяется так же, как и модуль рационально числа:
.
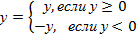Пример 1: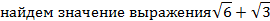 
Воспользуемся калькулятором:
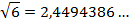
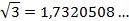
Найдем значение данного выражения с точностью до единиц.
Округлим полученные результаты до десятых:
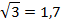
Тогда получаем:
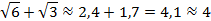
Найдем значение данного выражения с точностью до десятых.
Округлим полученные результаты до сотых:
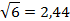
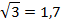3
Тогда получаем:
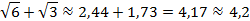
Найдем значение данного выражения с точностью до сотых.
Округлим полученные результаты до тысячных:
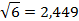
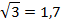32
Тогда получаем:
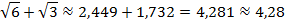и т.д.
Пример 2.
Давайте выясним, является ли последовательность бесконечно убывающей геометрической прогрессией, если она задана формулой:
а)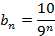 
; б)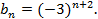 
Решение:
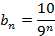. Найдем q.
; 
; 
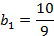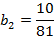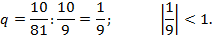
Следовательно, данная геометрическая прогрессия является бесконечно убывающей.
б)
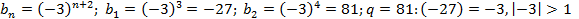
Следовательно, данная последовательность не является бесконечно убывающей геометрической прогрессией.
Действительные числа
Одним из самых основных понятий в математике является число.
Натуральные числа: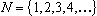 
.
Целые числа: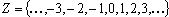 
.
Рациональные числа: Q = { m/n, где m – целое число, а n – натуральное}.
Можно также считать, что рациональные числа - это бесконечные периодические десятичные дроби.
Иррациональные числа – это числа, не представимые в виде обыкновенной дроби, т.е. бесконечные непериодические десятичные дроби. Например: π = 3,1416…, е = 2,7182…;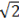 
=1,4142…
Все эти числа называют действительными числами – R.
Определение модуля числа: 
.
|
|
Основное свойство дроби: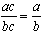 
.
Основное свойство пропорции: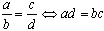 
.
Определение процента: 1% - это 1/100 часть числа.
Пример 3. Сократить дробь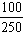 
.
Решение:
В соответствии с основным свойством дроби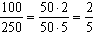 
.
Ответ: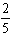 
.
Пример 4. Вычислите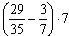 
.
Решение:
.
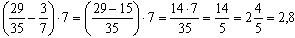Ответ: 2,8.
Пример 5. Влажность сухой цементной смеси на складе составляет 18%. Во время перевозки из-за дождей влажность смеси повысилась на 2%. Найдите массу привезенной смеси, если со склада было отправлено 400 кг.
Решение:
400 ∙ 0,18 = 72 (кг) - масса влаги в цементе на складе;
400 – 72 = 328 (кг) - масса цемента без влаги (сухого);
328 ∙ 100: 80 = 410 (кг) - масса привезённой смеси со склада.
Ответ: 410 кг.
Пример 6. Вычислите |-9,6|+|-7,4|-2.
Решение:
На основании определения модуля
|-9,6|+|-7,4|-2 = 9,6 + 7,4 – 2 = 15.
Ответ: 15.
Пример 7. Найти х, если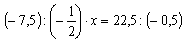 
.
Решение:
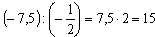; 22,5: (– 0,5) = – 225: 5 = – 45; 15 ∙ х = – 45; х = – 45: 15 = – 3.
Ответ: – 3.