Тема: Работа по перемещению проводника с током в магнитном поле.

Задачи урока:

Активизация мыслительной деятельности, формирование мышления; развитие умений сравнивать, выявлять закономерности, обобщать, логически мыслить. Воспитание ответственного отношения к учебному труду, активизация познавательного интереса учащихся, воспитание отношения к информации как к третьей сущности мира наряду с веществом и энергией.

Изучить лекцию и составить краткий конспект в теnрадях:

Рассмотрим контур с током, образованный неподвижными проводами и скользящей по ним подвижной перемычкой длиной l (рис. 2.17). Этот контур находится во внешнем однородном магнитном поле , перпендикулярном к плоскости контура. При показанном на рисунке направлении тока I, вектор сонаправлен с .

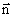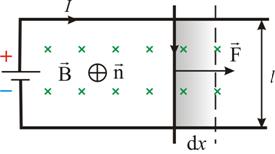
Рис. 2.17

На элемент тока I (подвижный провод) длиной l действует сила Ампера, направленная вправо:

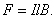
Пусть проводник l переместится параллельно самому себе на расстояние d x. При этом совершится работа:

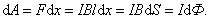
Итак,

,

(2.9.1)

Работа, совершаемая проводником с током при перемещении, численно равна произведению тока на магнитный поток, пересечённый этим проводником.

Формула остаётся справедливой, если проводник любой формы движется под любым углом к линиям вектора магнитной индукции.

Выведем выражение для работы по перемещению замкнутого контура с током в магнитном поле.

Рассмотрим прямоугольный контур с током 1-2-3-4-1 (рис. 2.18). Магнитное поле направлено от нас перпендикулярно плоскости контура. Магнитный поток , пронизывающий контур, направлен по нормали 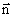к контуру, поэтому .

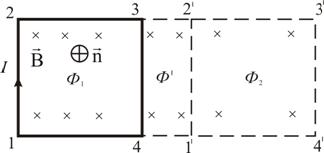
Рис. 2.18

Переместим этот контур параллельно самому себе в новое положение 1'-2'-3'-4'-1'. Магнитное поле в общем случае может быть неоднородным и новый контур будет пронизан магнитным потоком .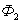

Площадка 4-3-2'-1'-4, расположенная между старым и новым контуром, пронизывается потоком .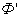

Полная работа по перемещению контура в магнитном поле равна алгебраической сумме работ, совершаемых при перемещении каждой из четырех сторон контура:

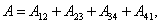
где , равны нулю, т.к. эти стороны не пересекают магнитного потока, при своём перемещение (очерчивают нулевую площадку).

.

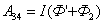Провод 1–2 перерезает поток (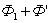), но движется против сил действия магнитного поля.

.

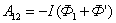Тогда общая работа по перемещению контура

или

,

(2.9.2)

здесь 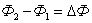– это изменение магнитного потока, сцепленного с контуром.

Работа, совершаемая при перемещении замкнутого контура с током в магнитном поле, равна произведению величины тока на изменение магнитного потока, сцепленного с этим контуром.

Элементарную работу по бесконечно малому перемещению контура в магнитном поле можно найти по формуле

,

(2.9.5)

Выражения (2.9.1) и (2.9.5) внешне тождественны, но физический смысл величины d Ф различен.

Соотношение (2.9.5), выведенное нами для простейшего случая, остаётся справедливым для контура любой формы в произвольном магнитном поле. Более того, если контур неподвижен, а меняется 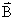, то при изменении магнитного потока в контуре на величину dФ, магнитное поле совершает ту же работу