ЛЕКЦИЯ 5
ВЕКТОРЫНА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ.
Вектором называется направленный отрезок  с началом в точке А и концом в точке В (который можно перемещать параллельно самому себе).
с началом в точке А и концом в точке В (который можно перемещать параллельно самому себе).

Длиной (или модулем) вектора  называется число
называется число  , равное длине отрезка
, равное длине отрезка  .
.
Векторы, лежащие на одной или на параллельных прямых, называются коллинеарными.
Если начало и конец вектора совпадают, например  , то вектор называется нулевым и обозначается
, то вектор называется нулевым и обозначается  .
.
Длина нулевого вектора равна нулю:  . Считаем, что нулевой вектор коллинеарен любому вектору.
. Считаем, что нулевой вектор коллинеарен любому вектору.
Действия с векторами:
1. Произведение вектора 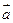 на число
на число  называется вектор
называется вектор 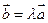 , имеющий длину
, имеющий длину  , направление которого совпадает с направлением
, направление которого совпадает с направлением 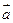 , если
, если  >0, и противоположно ему, если
>0, и противоположно ему, если  <0.
<0.
2. Суммой двух векторов 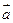 и
и  называется вектор
называется вектор 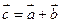 , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора 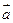 , а конец совпадает с концом вектора
, а конец совпадает с концом вектора  при условии, что начало вектора
при условии, что начало вектора  совпадает с концом вектора
совпадает с концом вектора 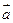 (правило треугольника).
(правило треугольника).
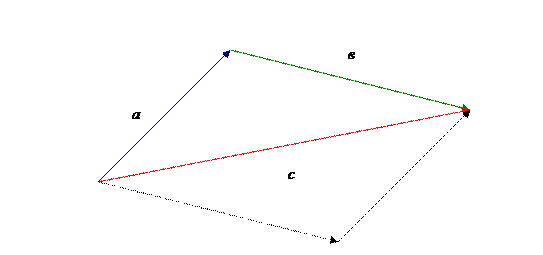
В этом случае вектор  является диагональю параллелограмма
является диагональю параллелограмма
(правило параллелограмма).
3. Скалярным произведением двух векторов определяется равенством: 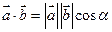 где
где  - угол между векторами
- угол между векторами 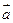 и
и  .
.
4. Проекцией вектора  на вектор
на вектор 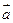 называется число
называется число 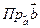 , равное длине вектора
, равное длине вектора  , если векторы
, если векторы 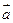 и
и  одинаково направлены, и равное длине вектора
одинаково направлены, и равное длине вектора  со знаком «-», если векторы
со знаком «-», если векторы 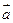 и
и  направлены в разные стороны. Проекция находится по формуле:
направлены в разные стороны. Проекция находится по формуле: 
Следствие:  .
. 
Проекция суммы двух векторов равна сумме проекций:


Свойства скалярного произведения векторов.
1. 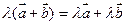 , где
, где 
следует из определения.
2. 
3. 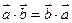
следует из определения.
4. 
следует из свойства проекций.
5.  ,
,  (условие перпендикулярности двух векторов)
(условие перпендикулярности двух векторов)
Доказательство:  .
.
5. 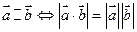 , для
, для  (условие коллинеарности двух векторов)
(условие коллинеарности двух векторов)
Доказательство: 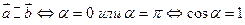 или
или 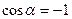 (так как угол между векторами
(так как угол между векторами  ).
).
7. 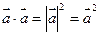 , или
, или 
следует из св-ва 6.
Координаты вектора.
Пусть  - единичные векторы системы координат в трехмерном пространстве, то есть
- единичные векторы системы координат в трехмерном пространстве, то есть  . Векторы
. Векторы  направлены по осям OX, OY, OZ соответственно.
направлены по осям OX, OY, OZ соответственно.
На плоскости система координат имеет две перпендикулярные оси OX и OY. Поэтому плоскость является двухмерным пространством.
Определение. Проекции вектора 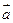 на единичные векторы системы координат называются координатами вектора
на единичные векторы системы координат называются координатами вектора 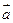 .
.
Координаты вектора в пространстве определяются тройкой чисел  .
.
Координаты вектора на плоскости определяются двумя числами  .
.
Пусть даны 2 вектора: 
Теорема. 
Доказательство:  .
.
Тогда: 

 .
.
Мы использовали, что  ,
,  .
.
Следствие:  , где
, где 
Доказательство: 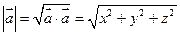 .
.
ЛЕКЦИЯ 6
Векторное произведение двух векторов.
Векторным произведением двух векторов 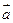 и
и  называется вектор
называется вектор  , удовлетворяющий условиям:
, удовлетворяющий условиям:
1.  ;
;  .
.
2.  , то есть длина вектора
, то есть длина вектора  равна площади параллелограмма, построенного на векторах
равна площади параллелограмма, построенного на векторах 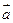 и
и  .
.
3. Направление вектора  определяется таким образом, что если смотреть с конца вектора
определяется таким образом, что если смотреть с конца вектора  на плоскость, в которой расположены вектора
на плоскость, в которой расположены вектора 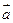 и
и  , то кратчайшее направление вращения вектора
, то кратчайшее направление вращения вектора 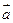 до совпадения с направлением вектора
до совпадения с направлением вектора  будет осуществляться против часовой стрелки.
будет осуществляться против часовой стрелки.
В дальнейшем мы будем говорить, что векторы 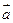 ,
,  и
и  образуют правую тройку.
образуют правую тройку.
Свойства.
1.  (антикоммутативность).
(антикоммутативность).
2.  .
.
3.  .
.
4.  .
.
5.  ;
;  .
.
Следуют из определения векторного произведения.
Если известны координаты векторов  , то векторное произведение можно найти, записав символический определитель, который разложим по 1-й строке:
, то векторное произведение можно найти, записав символический определитель, который разложим по 1-й строке:  =
=  =
=  .
.
Доказательство: 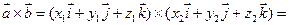
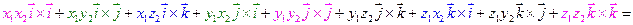

 .
.
Мы использовали соотношения 5.
Смешанное произведение трех векторов
Определение. 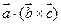 - смешанное произведение векторов.
- смешанное произведение векторов.
Если известны координаты векторов  ;
;  , то смешанное произведение можно найти по формуле:.
, то смешанное произведение можно найти по формуле:. 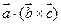 =
=  .
.
Доказательство:  ;
; 
. 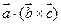 =
=  =
=  .
.
Теорема. Объем параллелепипеда, построенного на векторах  , исходящих из одной точки равен модулю смешанного произведения векторов
, исходящих из одной точки равен модулю смешанного произведения векторов  , то есть
, то есть  .
.
Доказательство. Пусть  .
.
Тогда 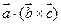 =
=  =
= 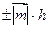 =
= 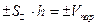 . Следовательно,
. Следовательно,  .
.
Условие компланарности трех векторов 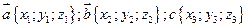 :
:
 или
или 
Вернемся к условиям перпендикулярности и коллинеарности и векторов и запишем их в координатах. Пусть даны 2 вектора: 
1. 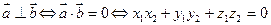 .
.
2.  , где
, где 
 .
.
Замечание. Если какая-либо координата одного вектора =0, то соответствующая координата другого вектора также =0. Например, если  , то
, то  .
.
Примеры.
1) При каких значениях n векторы  и
и  будут перпендикулярны?
будут перпендикулярны?
Решение.  ;
; 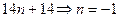 .
.
2) При каких значениях m и n векторы 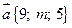 и
и  будут коллинеарны?
будут коллинеарны?
Решение. Запишем условие коллинеарности:  ;
; 
 .
.
3) Пусть 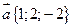 ;
;  .
.
Найти а)  ; б)
; б)  ; в) угол между векторами
; в) угол между векторами 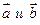
Решение. а)  . б)
. б)  .
.
в) 
 .
.
4) Найти векторное произведение векторов  и
и  .
.
Решение.  =
=  или
или  .
.
Определение. Координатами точки на плоскости (в пространстве) называются координаты ее радиус-вектора. 
Пусть даны две точки на плоскости:  и
и  . Тогда координаты вектора
. Тогда координаты вектора 

Доказательство.  . Но
. Но 

 .
.