Окружность.
Опр. Окружностью называется множество точек плоскости, находящихся на одинаковом расстоянии от данной точки, называемой центром.
Окр. (O; r).
О – центр окружности.
ВС – хорда.
ОА – радиус.
AD – диаметр.
DOE – сектор.
Опр. Часть плоскости, ограниченная окружностью, называется кругом.
P.S. Окружность – граница круга.
Опр. Радиусом называется отрезок, соединяющий центр с любой точкой окружности.
Опр. Хордой называется отрезок, соединяющий 2 любые точки окружности.
Опр. Диаметром называется хорда, проходящая центр.
Опр. Сектором называется часть круга, ограниченная радиусами.
Опр. Сегментом называется часть круга, ограниченная хордой.
P.S. Любая хорда образует 2 сегмента.
Опр. Дугой называется часть окружности, ограниченная 2-мя точками.
Взаимное расположение прямой и окружности.
d – расстояние от центра окружности до прямой.
r – радиус окружности.
I. Две общие точки.
d < r.
р – секущая.
II. Одна общая точка.
d = r.
р – касательная.
А – точка касания.
III. Нет общих точек.
d > r.
OA = d.
OB = r.
Касательная к окружности.
Опр. Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности. Их общая точка называется точкой касания прямой и окружности.
Свойства касательной.
1) Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Дано: окр.(О; R = ОА).
р – касательная.
А – точка касания.
Доказать: 
Доказательство:
Будем доказывать методом от противного.
Предположим, что ОА не перпендикулярна р. Тогда перпендикуляр, проведенный из точки О к прямой р меньше, чем ОА (перпендикуляр всегда меньше наклонной). Значит, ОА – наклонная. Поэтому прямая имеет с окружностью 2 общие точки. Тогда р – секущая, а по условию р – касательная. Получим противоречие. Наше предположение неверно. Значит,
|
|
Что и требовалось доказать.
2) Отрезки касательных к окружности, проведенные из одной точки, равны.
Дано: окр.(О; R).
АМ и AN – касательные.
M и N – точки касания.
Доказать: AM = AN.
Доказательство:
I) Д.П.: OM и ON – радиусы, ОА.
II) Рассмотрим 
и 
- они прямоугольные по свойству 1.
1) OM = ON = R.
2) ОА – общая.
Из условий 1) и 2) получаем, что = по катету и гипотенузе. Тогда AM = AN. Ч. и т.д.
3) Отрезки касательных к окружности, проведенные из одной точки, составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Дано: окр.(О; R). АМ.
AN – касательная.
M и N – точки касания.
Доказать: 
Доказательство:
I) Д.П.: OM и ON – радиусы, ОА.
II) Рассмотрим и - они прямоугольные по свойству 1.
1) OM = ON = R.
2) ОА – общая.
Из условий 1) и 2) получаем, что = по катету и гипотенузе. Тогда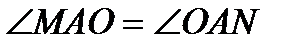 
.
Что и требовалось доказать.
Признак касательной.
(теорема, обратная свойству 1)
Теорема:
Прямая, проведенная через конец радиуса и перпендикулярная радиусу, является касательной.
Дано: окр.(О; R = ОА).
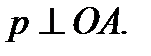
Доказать: р – касательная.
Доказательство:
Так как радиус является перпендикуляром к прямой, то d = R. А это означает, что прямая имеет с окружностью 1 общую точку. Значит, р – касательная.
Что и требовалось доказать.
Способ построения касательной.
Если точка лежит на окружности и через нее нужно провести касательную, то поступают следующим образом:
1) Проводят в эту точку радиус.
2) Восстанавливают перпендикуляр к радиусу.
|
|
Получаем касательную по признаку.