I. Теорема об отрезках пересекающихся хорд.
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой.
Дано: окр.(О; R).
АВ, CD – хорды.
Доказать: 
Доказательство:
1) Д.П.: AD, CB – хорды.
2) Рассмотрим 
.
(как вертикальные).
.
Отсюда 
(по 2-м углам).
Тогда 
. По свойству пропорции
Что и требовалось доказать.
II. Свойство угла, образованного хордой и касательной.
Угол, образованный хордой и касательной, измеряется половиной дуги, заключенной внутри угла.
Дано: окр.(О; R).
АВ – хорда.
р – касательная, А – точка касания.
Доказать: 
͜ АВ.
Доказательство:
1) Д.П.: AD – диаметр.
2)
Что и требовалось доказать.
III. Теорема о свойствах дуг, заключенных между параллельными хордами.
Градусные меры дуг, заключенных между параллельными хордами равны.
Дано: окр.(О; R).
АВ и CD – хорды.
АВ ǁ CD
Доказать: 
.
Доказательство:
1) Д.П.: AD – хорда.
2) 
(как накрест лежащие углы при параллельных прямых АВ и CD и секущей AD)
3) 
(по теореме о вписанном угле). Тогда 
. Отсюда
Что и требовалось доказать.
IV. Свойство перпендикуляра, проведенного к диаметру.
Перпендикуляр, проведенный к диаметру – есть среднеепропорциональное между отрезками диаметра.
Дано: окр.(О; R).
АВ – диаметр.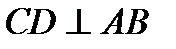 
Доказать: 
Доказательство:
1) Д.П.: AС и ВС – хорды
2) 
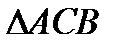- прямоугольный (по теореме о вписанном угле). Тогда 
Следствие (задача на построение отрезка, пропорционального двум данным).
Задача: Построить отрезок, средний пропорциональный между двумя данными.
Дано:
Построить:
Построение:
1) Проведем прямую т.
2) Отложим отрезок a + b.
3) 
4) окр.(О; R = ОА).
5) 
Доказательство: 
(по свойству IV).
Исследование: задача имеет единственное решение.
|
|
V. Свойство касательной и секущей.
Квадрат отрезка касательной равен произведению отрезков секущей, если касательная и секущая не параллельны.
Дано: окр.(О; R).
АВ – касательная. В – точка касания.
PQ(AQ) – секущая, 
Доказать: 
Доказательство:
1) Д.П.: BQ и BP – хорды.
2) Рассмотрим 
и 
.
- общий.
.
3) Отсюда ~ (по 2-м углам).
Тогда 
. По свойству пропорции
Что и требовалось доказать.
Следствие.
Если из одной точки к окружности провести две секущие, то произведение отрезков одной секущей равно произведению отрезков другой.
Дано: окр.(О; R).
АС и АЕ – секущие.
Доказать: 
Доказательство:
1) Д.П.: касательная АМ.
2) 
Тогда
Что и требовалось доказать.
VI. Свойство угла, образованного секущими (точка пересечения внутри круга).
Если две секущие пересекаются внутри круга, то угол, образованный этими секущими, равен полусумме дуг, заключенных внутри угла.
Дано: окр.(О; R).
АС и BD – секущие.
Доказать:
VII. Свойство угла, образованного секущими (точка пересечения вне круга).
Если две секущие пересекаются вне круга, то угол, образованный этими секущими, равен полуразности дуг, заключенных внутри угла.
Дано: окр.(О; R).
АС и BD – секущие.
Доказать:
Построение касательной к окружности, проходящей через точку, не лежащую на окружности.
Построение:
1) 
ОА.
2) ОМ = МА.
3) окр.(М; R = ОМ) 
окр.(О; R) = 
.
4) АВ и АС – касательные.
Доказательство:
I. Д.П.: ОВ и ОС – хорды.
II. 
(по свойству 1).
III. АВ и АС – касательные (по пр.). Что и требовалось доказать.
Исследование: задача всегда имеет 2 решения.