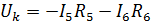ПОСТАНОВКА ЗАДАЧИ
Для схемы, соответствующей номеру варианта, разработать алгоритм и составить программу, которая предусматривает:
1. Расчет токов в ветвях по законам Кирхгофа.
2. Проверку баланса мощностей.
3. Построение потенциальной диаграммы для любого замкнутого контура, включающего источник ЭДС.
Сделать проверочные расчеты:
1. Расчет токов в ветвях матричным методом.
2. Промоделировать процессы в электрической схеме в среде Simulink.
Систему линейных уравнений с неизвестными токами решить методом Гаусса. Для этого создать универсальную собственную функцию. Расчеты проводить в среде пакета Matlab.
Таблица 1.1 – Исходные данные
| № вар. | 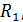 Ом
Ом
| 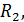 Ом
Ом
| 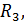 Ом
Ом
| 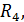 Ом
Ом
| 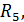 Ом
Ом
| 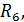 Ом
Ом
| 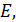 В
В
| 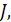 А
А
|
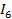
|
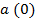
|
| 3 к. |
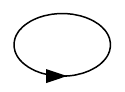
| 2 к. |
| 1 к. |
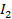
|
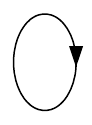

 (2) (2)
|
|
 (1) (1)
|
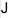
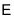
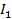
|

|
|


|
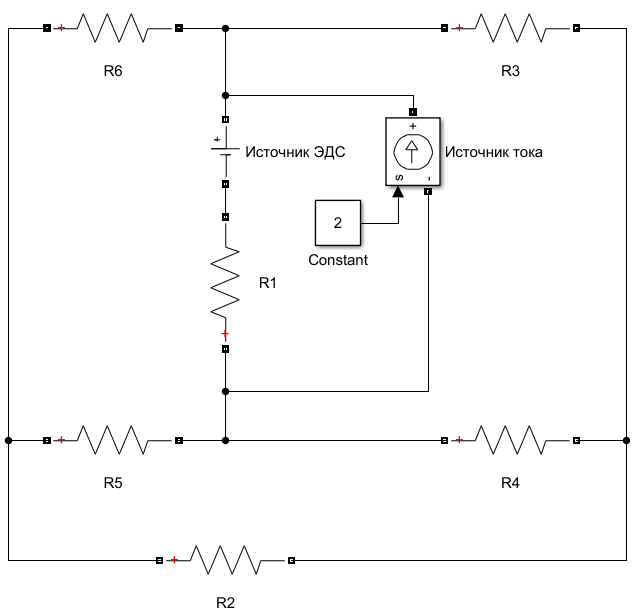
Рисунок 1.1 – Электрическая цепь
2 РЕШЕНИЕ ЗАДАЧИ
2.1 Расчет токов по законам Кирхгофа
Первый закон Кирхгофа устанавливает зависимость между токами для узлов электрической цепи, к которым подходит несколько ветвей. Согласно этому закону алгебраическая сумма токов ветвей, сходящихся в узле электрической цепи, равна нулю.
При этом токи, направленные к узлу, берут с одним знаком (например, положительным), а токи, направленные от узла – с противоположным знаком (отрицательным).
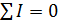
Число независимых уравнений, составленных по 1-му закону Кирхгофа, составляет 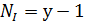 , где
, где  – число узлов в схеме.
– число узлов в схеме.
Второй закон Кирхгофа устанавливает зависимость между ЭДС и напряжением в замкнутой электрической цепи. Согласно этому закону во всяком замкнутом контуре алгебраическая сумма ЭДС равна алгебраической сумме падений напряжения на сопротивлениях, входящих в этот контур. При составлении формул, характеризующих второй закон Кирхгофа, значения ЭДС 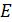 и падений напряжений
и падений напряжений 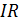 считают положительными, если направления ЭДС и токов на соответствующих участках контура совпадают с произвольно выбранным направлением обхода контура. Если же направления ЭДС и токов на соответствующих участках контура противоположны выбранному направлению обхода, то такие ЭДС и падения напряжения считают отрицательными.
считают положительными, если направления ЭДС и токов на соответствующих участках контура совпадают с произвольно выбранным направлением обхода контура. Если же направления ЭДС и токов на соответствующих участках контура противоположны выбранному направлению обхода, то такие ЭДС и падения напряжения считают отрицательными.
Число независимых уравнений, составленных по 2-му закону Кирхгофа, составляет 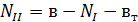 , где
, где 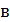 – число ветвей с неизвестными токами в схеме,
– число ветвей с неизвестными токами в схеме, 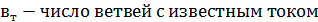 .
.
Уравнения составляются для независимых контуров.
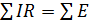
Таким образом, получаем систему 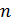 линейных уравнений с
линейных уравнений с 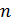 неизвестными, которую можно решить любым из известных методов. Ток в ветви может иметь отрицательное значение. Это означает, что действительное направление тока противоположно выбранному в начале расчета произвольно направлению.
неизвестными, которую можно решить любым из известных методов. Ток в ветви может иметь отрицательное значение. Это означает, что действительное направление тока противоположно выбранному в начале расчета произвольно направлению.
Рассмотрим случай, указанный в задании. В схеме 4 узла, 7 ветвей, 1 ветвь с известным током. Необходимо составить 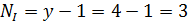 уравнения по 1-му закону Кирхгофа и
уравнения по 1-му закону Кирхгофа и 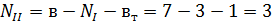 уравнения по 2-му.
уравнения по 2-му.
Cоставим систему из 3-х уравнений по 1-му закону Кирхгофа для 3-х узлов:
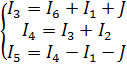
Также составим систему из 3-х уравнений по 2-му закону Кирхгофа для 3-х контуров:
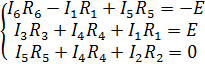
В ходе подстановки уравнений, составленных по 1-му закону Кирхгофа в систему по 2-му, получим следующую СЛАУ:
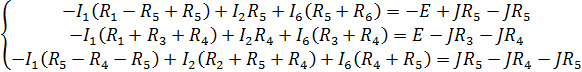
Решив полученную СЛАУ методом Гаусса, определим значение токов 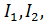 и
и 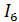 . Затем определим токи
. Затем определим токи 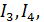 и
и 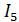 при помощи известных уравнений по 1-му закону Кирхгофа.
при помощи известных уравнений по 1-му закону Кирхгофа.
Расчет токов матричным методом
Матричный метод расчета токов в ветвях разветвленных электрических цепей, по сути, представляет собой формализацию метода контурных токов, известного из электротехники.
Вначале необходимо определить параметры цепи:
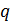 – количество узлов в схеме;
– количество узлов в схеме;
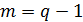 – количество независимых узлов;
– количество независимых узлов;
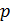 – количество ветвей с неизвестными токами;
– количество ветвей с неизвестными токами;
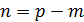 – количество независимых контуров.
– количество независимых контуров.
Для каждой ветви выбирается положительное направление тока, для каждого контура – положительное направление обхода.
Записываются векторы-столбцы ЭДС 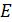 размером (
размером (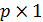 ) и источников тока
) и источников тока 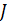 размером (
размером (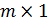 ), составляется квадратная диагональная матрица сопротивлений ветвей
), составляется квадратная диагональная матрица сопротивлений ветвей 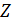 размером (
размером (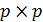 ).
).
После этого составляется матрица независимых контуров 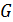 размером (
размером (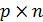 ) по принципу:
) по принципу:

и матрица соединений 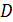 размером (
размером (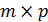 ):
):

Запишем уравнения в матричной форме по законам Ома и по I и II законам
Кирхгофа:
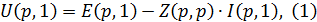
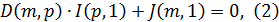
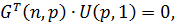
Умножив уравнение 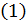 на
на 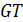 слева, имеем:
слева, имеем:
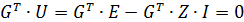 ,
,
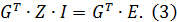
Если объединить уравнения 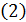 и
и 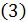 в одну систему, получим:
в одну систему, получим:
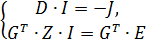
Обозначив матрицу коэффициентов как 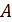 и вектор свободных членов как
и вектор свободных членов как 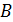 :
:
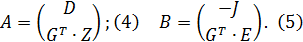
получаем систему линейных уравнений в матричном виде 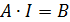 , которую можно решить любым известным методом.
, которую можно решить любым известным методом.
Сформируем указанные матрицы, используя данный метод.
Векторы-столбцы источников ЭДС 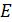 и тока
и тока 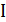 , а также матрица сопротивлений ветвей
, а также матрица сопротивлений ветвей 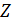 будут иметь следующей вид для данной цепи:
будут иметь следующей вид для данной цепи:
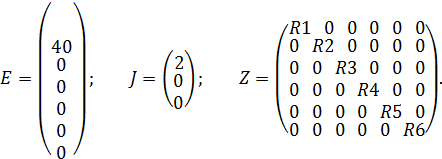
Составим матрицу независимых контуров 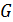 для независимых контуров 1, 2 и 3 и матрицу соединений
для независимых контуров 1, 2 и 3 и матрицу соединений 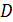 для независимых узлов 1, 2, 3, обозначенных на рис. 1.1.
для независимых узлов 1, 2, 3, обозначенных на рис. 1.1.
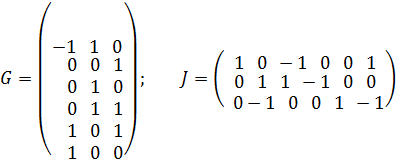
Составив матрицу коэффициентов 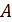 и вектор свободных членов
и вектор свободных членов 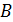 , воспользуемся формулами (4) и (5), соответственно:
, воспользуемся формулами (4) и (5), соответственно:
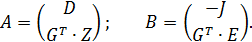
Решим полученную матрицу при помощи метода Гаусса получим результаты.
2.3 Построение потенциальной диаграммы
Потенциальная диаграмма является одной из проверок вычисления токов в ветвях. При обходе какого-либо замкнутого контура потенциал узла, с которого начинается обход, принимается равным нулю, и если после завершения обхода последний потенциал (то есть потенциал, с которого начинался обход) равен нулю, то токи в контуре рассчитаны правильно.
Для построения потенциальной диаграммы 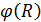 надо рассчитать вектор потенциалов (по закону Ома) и соответствующий ему вектор сопротивлений по направлению обхода контура.
надо рассчитать вектор потенциалов (по закону Ома) и соответствующий ему вектор сопротивлений по направлению обхода контура.
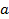
|
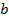
|
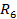
|
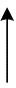
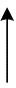
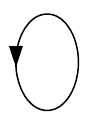
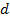
|
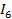
|
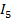
|
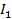
|

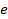
|
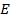
|
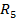
|
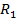
|
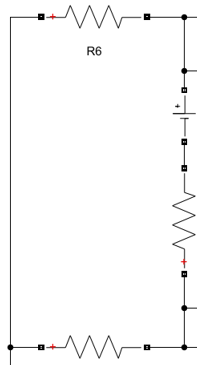
Рисунок 2.1 – Контур электрической цепи
Примем 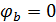 , тогда:
, тогда:
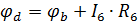
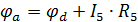
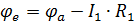
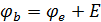
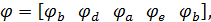
и соответствующий вектор сопративлений будет равен:
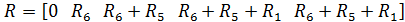
2.3 Проверка баланса мощностей
Для проверки результата вычисления токов ветвей в электрической цепи необходимо рассчитать баланс мощностей. Для любых замкнутых цепей сумма мощностей источников электрической энергии 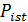 равна сумме мощностей, расходуемых в приемниках энергии
равна сумме мощностей, расходуемых в приемниках энергии 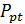 .
.
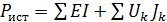
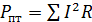
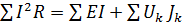
Если направление тока 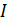 , протекающего через источник ЭДС
, протекающего через источник ЭДС 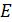 , совпадает с направлением ЭДС, то источник ЭДС доставляет в цепь мощность равную
, совпадает с направлением ЭДС, то источник ЭДС доставляет в цепь мощность равную 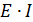 с положительным знаком. Если направление тока
с положительным знаком. Если направление тока 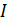 встречно направлению источника ЭДС
встречно направлению источника ЭДС 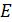 , то источник ЭДС не доставляет в цепь энергию, а потребляет ее, и мощность
, то источник ЭДС не доставляет в цепь энергию, а потребляет ее, и мощность 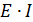 войдет в уравнение энергетического баланса с отрицательным знаком.
войдет в уравнение энергетического баланса с отрицательным знаком.
Если схема питается не только от источников ЭДС, но и от источников тока 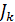 , при составлении уравнения энергетического баланса необходимо учесть и энергию, доставляемую источниками тока. Для этого следует найти напряжение на зажимах источников тока
, при составлении уравнения энергетического баланса необходимо учесть и энергию, доставляемую источниками тока. Для этого следует найти напряжение на зажимах источников тока 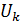 .
.
Баланс мощностей не должен превышать 5 %.
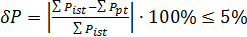
Для исходной электрической цепи уравнение энергетического баланса будет иметь вид:
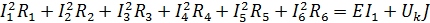
По 2-му закону Кирхгофа 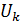 в данной электрической цепи равен:
в данной электрической цепи равен: