В ходе выполнения курсовой работы была составлена следующая модель электрической схемы в Simulink:
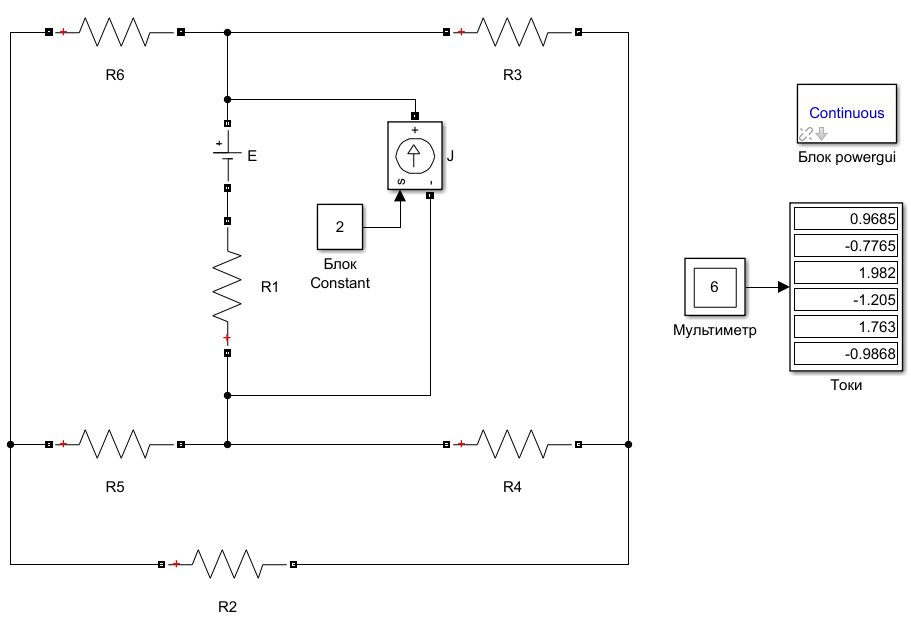
Рисунок 2.5 – Модель электрической схемы в Simulink и значения токов 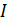
Как мы видим значения токов совпадают с теми, что были получены решением СЛАУ, составленной при помощи методов Кирхгофа.
3 МАТЕМАТИЧЕСКИЕ МЕТОДЫРАСЧЕТА
В практической деятельности специалистов электротехнической области очень часто случается рассчитывать разные параметры электрических схем. Математические модели таких схем в своем большинстве описываются системами линейных алгебраических уравнений (СЛАУ) с действительными коэффициентами.
Существуют разные методы решения таких задач. К наиболее распространенным и удобным при использовании вычислительной техники относятся методы Гаусса, Крамера и обратной матрицы. В данной варианте будет использоваться метод Гаусса.
3.1 Метод Гаусса
В общем виде систему линейных алгебраических уравнений с действительными коэффициентами можно записать в виде:
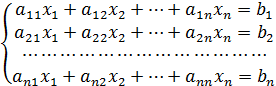
или в матричном виде: 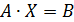 ,
,
где
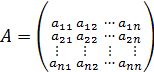 – квадратная матрица коэффициентов;
– квадратная матрица коэффициентов;
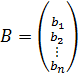 – вектор свободных членов;
– вектор свободных членов;
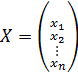 – искомый вектор корней;
– искомый вектор корней;
Целью решения такой системы и есть нахождение значений корней 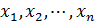 .
.
СЛАУ имеет единственное решение, если определитель 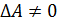 .
.
Метод Гаусса предусматривает решение задачи в два этапа:
1) на первом этапе, который называется прямой ход, выполняется последовательное исключение корней, начиная с первого (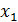 ) к предпоследнему (
) к предпоследнему (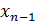 ), при этом матрица коэффициентов А из квадратной становится треугольной.
), при этом матрица коэффициентов А из квадратной становится треугольной.
2) на втором этапе, который называется обратный ход, выполняется последовательное вычисление корней из преобразованной на первом этапе системы уравнений в обратном направлении, начиная от последнего (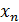 ) и к первому (
) и к первому (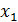 ).
).
После выполнения первого этапа система уравнений принимает вид:
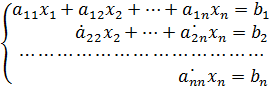
В этом случае, полученные после преобразований коэффициенты при неизвестных корнях и свободные члены будут иметь значения, которые отличаются от начальных, во всех уравнениях кроме первого. Они обозначены символом ( ).
).
В общем случае исключение 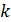 -го корня (
-го корня (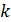 = 1, 2, 3,
= 1, 2, 3, 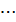 ,
, 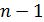 ) с
) с 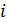 -го уравнения (
-го уравнения (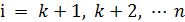 ) выполняется путем замены всех коэффициентов
) выполняется путем замены всех коэффициентов 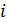 -го уравнения разностью между начальными коэффициентами этого уравнения (до преобразования) и соответствующими коэффициентами
-го уравнения разностью между начальными коэффициентами этого уравнения (до преобразования) и соответствующими коэффициентами 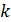 -го уравнения, умноженными на масштабный множитель, который вычисляется таким образом:
-го уравнения, умноженными на масштабный множитель, который вычисляется таким образом:
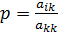 .
.
После преобразований коэффициенты 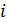 -го уравнения будут иметь следующие значения:
-го уравнения будут иметь следующие значения:
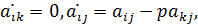
где 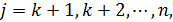
а свободный член:
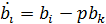 .
.
Вычисление корней на этапе обратного хода выполняется, начиная с последнего корня:
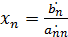 .
.
Затем, его значение 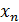 подставляется в предпоследнее уравнение и вычисляется корень
подставляется в предпоследнее уравнение и вычисляется корень 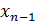 , и так далее до первого
, и так далее до первого 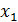 . В общем виде формула для вычисления корней СЛАУ имеет вид:
. В общем виде формула для вычисления корней СЛАУ имеет вид:
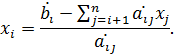
В рассмотренном выше варианте метода Гаусса могут возникнуть ситуации, когда решение не может быть найдено или иметь существенную погрешность: например, в случае если главный элемент равен 0, при нормализации возникает деление на 0; также существенно меньшее значение главного элемента по сравнению с остальными может привести к увеличению погрешности вычислений. Для исправления таких ситуаций применяют т.н. выбор главного элемента: выбор максимального значения главного элемента с последующей перестановкой строк и столбцов, или частный случай: выбор максимального значения главного элемента с последующей перестановкой строк.
Перестановка выполняется таким образом, чтобы модуль коэффициента 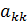 при исключаемом корне был максимальным.
при исключаемом корне был максимальным.
Алгоритм метода Гаусса можно упростить, если объединить квадратную матрицу коэффициентов 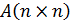 и вектор-столбец
и вектор-столбец 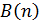 одну матрицу
одну матрицу 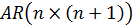 , которая называется расширенной матрицей коэффициентов. В ней
, которая называется расширенной матрицей коэффициентов. В ней 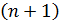 -й столбец составляют элементы вектора свободных членов
-й столбец составляют элементы вектора свободных членов 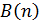 . Соответственно переменные
. Соответственно переменные 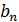 и
и 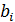 заменяются переменными
заменяются переменными 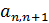 и
и  .
.
4 ОПИСАНИЕ АЛГОРИТМА
Блок-схема алгоритма основной программы (рис. Б.1) состоит из следующих блоков:
4 – Задание коэффициентов матрицы 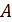 , созданной по законам Кирхгофа.
, созданной по законам Кирхгофа.
5 – Вызов функции для решения СЛАУ методом Гаусса.
6 – Вывод искомых токов 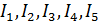 и
и 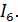
7 - 9 – Расчет баланса мощностей электрической цепи.
10 - 12 – Построение потенциальной диаграммы.
13 – Запись векторов-столбцов ЭДС 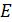 и источников тока
и источников тока 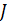 , а также матрицы сопротивлений ветвей
, а также матрицы сопротивлений ветвей 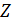 .
.
14 – Запись матрицы независимых контуров 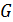 .
.
15 – Запись матрицы соединений 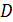 .
.
16 – Задание коэффициентов матрицы 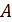 , созданной матричным методом.
, созданной матричным методом.
5 АНАЛИЗ РЕЗУЛЬТАТОВ
В результате выполнения программы, написанной на языке Matlab и решенной методом Гаусса, были получены следующие результаты:
Таблица 5.1 – Сравнение результатов в Matlab
| Токи в цепи | Метод законов Кирхгофа | Матричный метод |
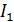 , А , А
| 0,9685 | 0,9685 |
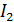 , А , А
| -0,7765 | -0,7765 |
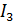 , А , А
| 1,9817 | 1,9817 |
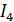 , А , А
| 1,2052 | 1,2052 |
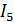 , А , А
| -1,7633 | -1,7633 |
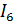 , А , А
| -0,9868 | -0,9868 |
Как можем видеть, значения абсолютно идентичны, что указывает на высокую точность математических расчетов.
По завершению создания модели электрической цепи, которая выполнена в графическом окружении Simulink, были получены идентичные значения токов:
Таблица 5.2 – Значения токов в модели Simulink
| Токи в цепи | Моделирование в Simulink |
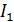 , А , А
| 0,9685 |
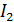 , А , А
| -0,7765 |
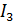 , А , А
| 1,982 |
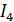 , А , А
| -1,205 |
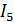 , А , А
| 1,763 |
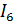 , А , А
| -0,9868 |
В программе Matlab была также произведена проверка баланса мощностей:
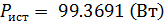
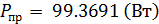
Суммарная мощность, вырабатываемая источниками электрической энергии равна сумме мощностей, потребляемой в цепи, что подтверждает правильность расчетов.
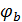
|
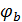
|
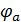
|
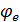
|
|
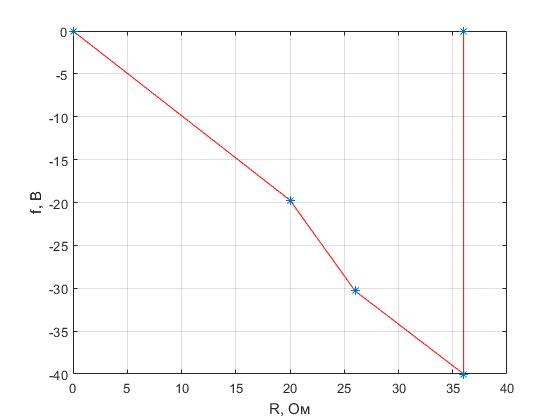
Рисунок 5.1 – Потенциальная диаграмма контура
Таблица 5.3 – Значения потенциалов на диаграмме
| Потенциалы | Значение, В |
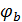
| |
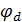
| -19.7358 |
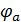
| -30.3154 |
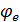
| -40 |
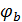
|
На рис. 5.1 видно, что при обходе замкнутого контура потенциал узла, с которого начинается обход (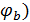 , равен нулю, и после завершения обхода последний потенциал (то есть потенциал
, равен нулю, и после завершения обхода последний потенциал (то есть потенциал 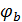 , с которого начинался обход) также равен нулю. Это доказывает то, что токи в контуре рассчитаны правильно.
, с которого начинался обход) также равен нулю. Это доказывает то, что токи в контуре рассчитаны правильно.
Можем сделать вывод, что полученные результаты с помощью программы, написанной в математической среде Matlab, полностью совпадают с данными, которые получены в графическом окружении Simulink, а также, что уравнения энергетического баланса и потенциальная диаграмма контура составлены верно и отражают корректность вычислений. Также можем обратить внимание, что искомые значения токов 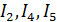 и
и 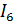 получились отрицательные. Это говорит о том, что фактическое направление токов на данном участке цепи обратно принятому. Сравнив результаты, делаем вывод, что погрешность вычислений не превышает 0,001 (А), то есть результат выполнения расчетов любым способом достаточно точен.
получились отрицательные. Это говорит о том, что фактическое направление токов на данном участке цепи обратно принятому. Сравнив результаты, делаем вывод, что погрешность вычислений не превышает 0,001 (А), то есть результат выполнения расчетов любым способом достаточно точен.
ЗАКЛЮЧЕНИЕ
В ходе выполнения курсовой работы были получены навыки пользования библиотеками Simulink математического пакета Matlab, закреплены знания в области ТОЭ и практические навыки работы с языком Matlab.
В результате выполнения курсовой работы была разработана программа, которая рассчитывает значения токов в электрической цепи при помощи метода Гаусса, выполняет проверку баланса мощностей, строит потенциальную диаграмму контура цепи. Программа производит вывод результата в консоль. Создана математическая модель электрической цепи в Simulink. Также составлены блок-схемы алгоритма программы и приведено их описание.
Можем сделать вывод, что использование Matlab и других современных пакетов прикладных программ для решения технических задач любой сложности существенно увеличивает точность и скорость нахождения результатов. Навыки по созданию алгоритмов и программ в пакете Matlab, полученные в ходе выполнения работы, могут использоваться в профессиональной деятельности современного инженера для решения более сложных заданий.
СПИСОК ЛИТЕРАТУРЫ
1. Дьяконов В.П. MATLAB R2006/2007/2008+Simulink 5/6/7: основы применения / В. П. Дьяконов - 2-е изд., перер. и доп. – М.: СОЛОН-ПРЕСС, 2008. 800с.: ил.
2. Курбатова Е.А. MATLAB 7 / Е.А. Курбатова – М.; СПб.; К.: Диалектика, 2006. – 256с.: ил.
3. Краскевич В.Е. Численные методы в инженерных исследованиях: учебное
пособие для вузов / В.Е. Краскевич, К.Х. Зеленский, В.И. Гречко – К.: Вища школа, 1986. - 263с.: граф.
4. Л.А. Бессонов. Теоретические основы электротехники. М. ВШ. 1973. 749с.
5. Теоретические основы электротехники / Под. ред. П.А. Ионкина. – М.:ВШ. 1976. – 383 с.
6. Основы теории цепей / Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. – М.: Энергоатомиздат. 1989. – 528 с.
ПРИЛОЖЕНИЕ А
Перечень замечаний нормоконтролера
cтудента Жука О.Е., группы ЭАПУ-20
| Обозначение документа | Документ | Условная оценка | Содержание замечания |
Дата ____________ Подпись __________________________
(Ф.И.О)
ПРИЛОЖЕНИЕ Б
Блок-схемы алгоритмов
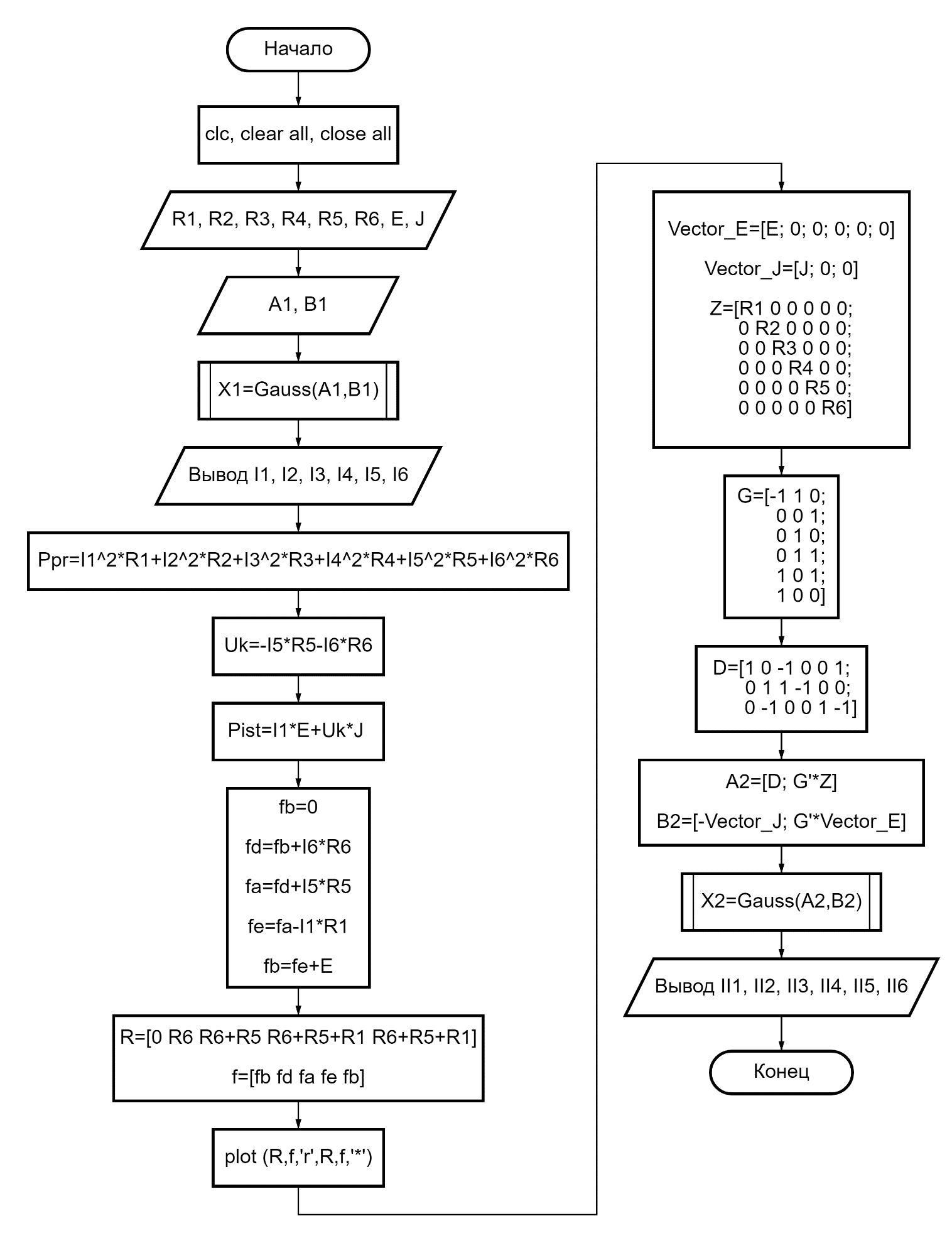
Рисунок Б.1 – Основная программа
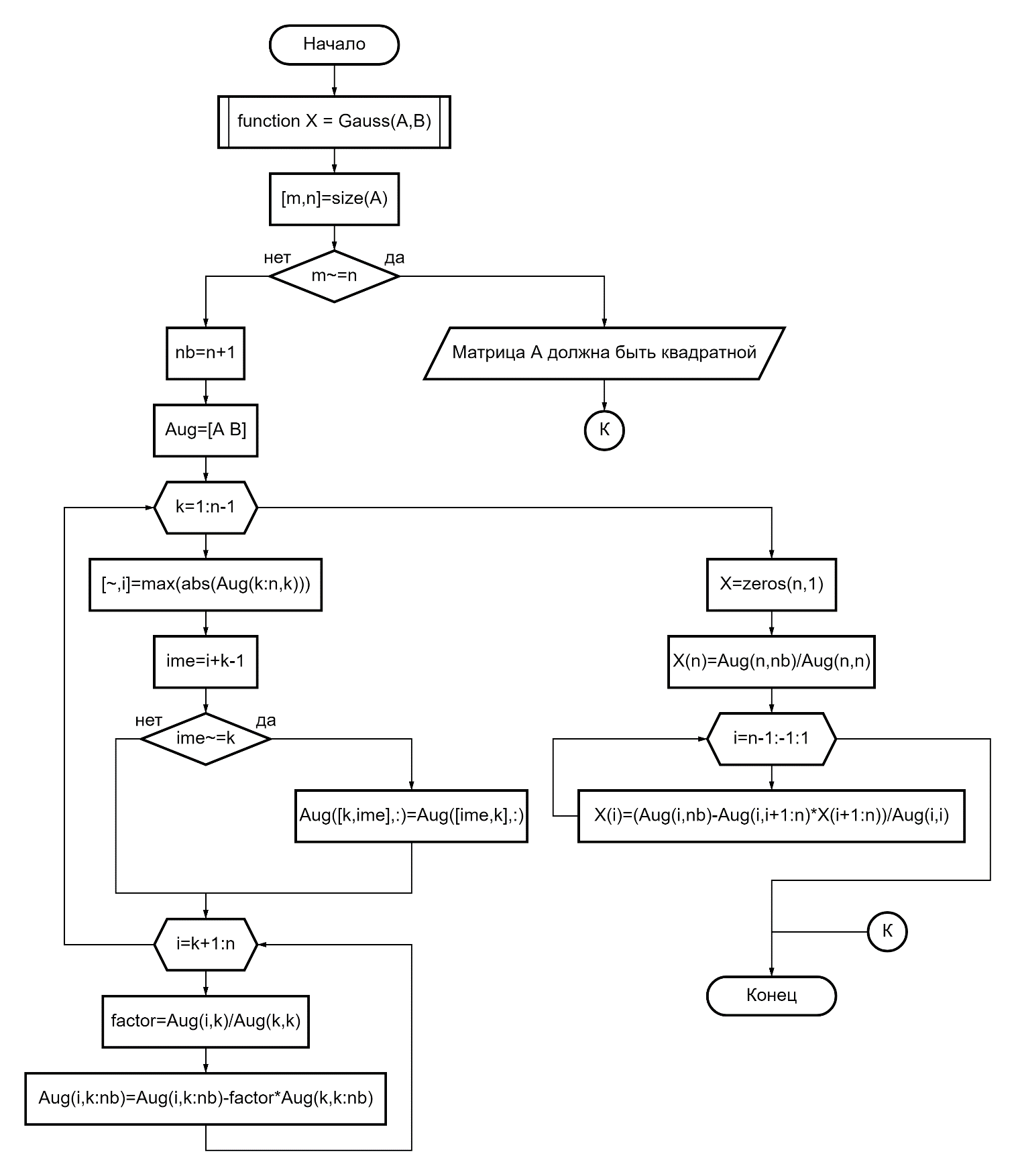
Рисунок Б.2 – Функция Gauss
ПРИЛОЖЕНИЕ В
Листинг программы
Program:
clc, clear all, close all
%Исходные данные:%
R1=10; R2=5; R3=8; R4=12; R5=6; R6=20; E=40; J=2;
disp('Матрица коэффициентов по законам Кирхгофа:')
A1=[-(R1+R5-R5) R5 (R5+R6); (R1+R3+R4) R4 (R3+R4); -(-R4+R5-R5) (R2+R4+R5) (R4+R5)]
B1=[-E+J*R5-J*R5; E-J*R3-J*R4; -J*R4+J*R5-J*R5]
disp('Результаты вычислений методом Гаусса:')
X1=Gauss(A1,B1);
I1=X1(1,:)
I2=X1(2,:)
I6=X1(3,:)
disp('Токи по 1-му закону Кирхгофа:')
I3=I6+I1+J
I4=I3+I2
I5=I4-I1-J
disp('Проверка баланса мощностей:')
Ppr=I1^2*R1+I2^2*R2+I3^2*R3+I4^2*R4+I5^2*R5+I6^2*R6
Uk=-I5*R5-I6*R6;
Pist=I1*E+Uk*J
disp('Построение потенциальной диаграммы:')
fb=0
fd=fb+I6*R6
fa=fd+I5*R5
fe=fa-I1*R1
fb=fe+E
R=[0 R6 R6+R5 R6+R5+R1 R6+R5+R1]; f=[fb fd fa fe fb];
figure(1)
plot (R,f,'r',R,f,'*'), grid on,
xlabel('R, Ом'), ylabel('f, В')
disp('Результаты вычислений матричным методом:')
Vector_E=[E; 0; 0; 0; 0; 0];
Vector_J=[J; 0; 0];
Z=[R1 0 0 0 0 0; 0 R2 0 0 0 0; 0 0 R3 0 0 0; 0 0 0 R4 0 0; 0 0 0 0 R5 0; 0 0 0 0 0 R6];
G=[-1 1 0; 0 0 1; 0 1 0; 0 1 1; 1 0 1; 1 0 0];
D=[1 0 -1 0 0 1; 0 1 1 -1 0 0; 0 -1 0 0 1 -1];
A2=[D; G'*Z]; B2=[-Vector_J; G'*Vector_E];
X2=Gauss(A2,B2);
II1=X2(1,:)
II2=X2(2,:)
II3=X2(3,:)
II4=X2(4,:)
II5=X2(5,:)
II6=X2(6,:)
Gauss:
function X = Gauss(A,B)
[m,n]=size(A);
if m~=n, error('Матрица A должна быть квадратной'); end
nb=n+1;
Aug=[A B];
for k=1:n-1
[~,i]=max(abs(Aug(k:n,k)));
ime=i+k-1;
if ime~=k
Aug([k,ime],:)=Aug([ime,k],:);
end
for i=k+1:n
factor=Aug(i,k)/Aug(k,k);
Aug(i,k:nb)=Aug(i,k:nb)-factor*Aug(k,k:nb);
end
end
X=zeros(n,1);
X(n)=Aug(n,nb)/Aug(n,n);
for i=n-1:-1:1
X(i)=(Aug(i,nb)-Aug(i,i+1:n)*X(i+1:n))/Aug(i,i);
end
ПРИЛОЖЕНИЕ Г
Результаты работы программы
Матрица коэффициентов по законам Кирхгофа:
A1 =
-10 6 26
30 12 20
12 23 18
B1 =
-40
-24
Результаты вычислений методом Гаусса:
I1 =
0.9685
I2 =
-0.7765
I6 =
-0.9868
Токи по 1-му закону Кирхгофа:
I3 =
1.9817
I4 =
1.2052
I5 =
-1.7633
Проверка баланса мощностей:
Ppr =
99.3691
Pist =
99.3691
Построение потенциальной диаграммы:
fb =
fd =
-19.7358
fa =
-30.3154
fe =
-40
fb =
Результаты вычислений матричным методом:
II1 =
0.9685
II2 =
-0.7765
II3 =
1.9817
II4 =
1.2052
II5 =
-1.7633
II6 =
-0.9868