При решении линейных динамических задач наиболее широкое применение нашел метод разложения искомой функции по собственным формам колебаний (в отечественной литературе этот метод часто именуется обобщенным методом Галеркина).
Рассмотрим типовое уравнение нагружения стержневых систем
| (5.1) |
Здесь m – погонная масса; w – перемещения, H – характеризует диссипацию, 
– погонная распределенная сила.
В случае продольного нагружения прямолинейного стержня
|
в случае поперечного нагружения прямолинейного стержня (балки)
|
Для удобства решения задачи будем считать, что функция w (x) удовлетворяет однородным граничным условиям, которые являются различными для каждой задачи.
Силы и моменты, действующие в начальном или конечном сечениях балки, с использованием дельта-функций включаются внутрь области, в которой решается уравнение (5.1), и учитываются в правой части уравнения (5.1) и в обобщенных силах (5.18)-(5.22).
Начальные условия являются общими для различных типов задач. Задается начальное поле перемещения
| (5.2) |
и начальное поле скорости
| (5.3) |
Будем искать решение в следующем виде
| (5.4) |
Здесь 
– собственные формы колебаний рассматриваемой задачи, которые используются в качестве базисных функций,
– обобщенные координаты.
Остановимся на определении собственных частот и форм колебаний рассматриваемой задачи. Из уравнения (5.1) исключаются внешние и диссипативные силы и решение отыскивается в виде стационарной функции
 (i – мнимая единица).
| (5.5) |
Для форм колебаний получаем следующее уравнение
| (5.6) |
с однородными граничными условиями, соответствующими исходной задаче (5.1).
Известно, что в случае континуальной модели существует счетное множество собственных частот wi и соответствующих им форм колебаний 
. При этом из (5.6) очевидно, что собственные формы определяются с точностью до констант в виде множителей.
В связи с тем, что формы колебаний удовлетворяют граничным условиям задачи (5.1), решение, отыскиваемое в форме (5.4), также удовлетворяет граничным условиям.
Подставляя представление (5.4) (5.разложение по собственным формам колебаний) в уравнение (5.1) придем к следующему равенству
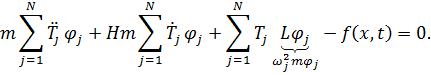
| (5.7) |
С учетом уравнения для собственных форм колебаний (5.6) равенство (5.7) преобразуется к следующему виду
| (5.8) |
Потребуем, чтобы выражение 
(5.8) было ортогонально ко всем собственным формам колебаний jn, которые образуют полную систему функций,
| (5.9) |
С учетом ортогональности собственных форм колебаний с весовой функцией в виде погонной массы m из суммы в равенстве (5.9) останется только n ‑ый член
| (5.10) |
где
| – обобщенная сила по n –му тону колебаний, | (5.10а) |
| – приведенная масса, | |
| – логарифмический декремент. |
Диссипативные члены 
вводятся в уравнение (5.10) на основе опыта, полученного при вибродинамических испытаниях объектов (см. раздел 2.5).
Из условия удовлетворения обобщенными координатами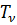 
уравнениям (5.10) следует тождественное равенство нулю П(x,t) из (5.8). Это означает, что функция (5.4) с учетом (5.10) является решением уравнения (5.1).
Для решения уравнений (5.10) необходимо определить начальные условия Tj (0) и 
. С этой целью подставим представления (5.4) в равенства (5.2) и (5.3).
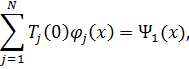
| (5.11) |
|
Умножаем скалярно левую и правую часть равенств (5.2) и (5.3)на 
с учетом ортогональности форм колебаний получаем начальные данные для интегрирования уравнений (5.10).
| (5.12) |
В случае пространственной конструкции со свободными краями для полноты системы базисных функций к упругим тонам колебаний добавляются шесть ортогонализированных тонов твёрдого тела 
и представление (5.4) примет вид
| (5.13) |
В этом случае к уравнениям (5.10) для обобщённых координат , соответствующих упругим тонам, добавится шесть уравнений, соответствующих твёрдым тонам. Предварительно должна быть проведена ортогонализация тонов твердого тела для получения распадающейся системы уравнений. Связано это с тем, что в пространственном случае шестикратной нулевой частоте твердого тела соответствует шесть линейно независимых функций
| (5.14) |
При этом обобщённая сила и приведённая масса определяются по формулам (5.10а), в которых формы упругих тонов заменяются на формы твёрдого тела .
К начальным значениям (5.12) добавятся начальные значения для обобщённых координат тонов твёрдого тела. В этих формулах необходимо заменить на 
.
После определения тонов упругих колебаний и тонов твёрдого тела, а также обобщённых координат решение задачи для перемещений завершается. Определение силовых факторов конструкции сводится к дифференцированию перемещений по координатам.
Дифференцирование рядов, как известно, приводит к ухудшению сходимости рядов. Поэтому для улучшения сходимости силовых факторов в отечественной практике используется метод выделения квазистатики, в зарубежных программных комплексах используется метод расширения базиса собственных функций "residual" векторами (см. раздел).
С учётом того, что формы колебаний jn (5.6) определяются с точностью до констант в виде множителей, в программных комплексах для удобства используется единичная нормировка приведённых масс Мn.
 .
| (5.15) |
Совокупность уравнений (5.10), (5.14) и начальных условий (5.12) позволяет определить обобщенные координаты 
.
Общее решение неоднородного дифференциального уравнения (5.10) с начальными данными (5.12) имеет вид
| (5.16) | |||
где  
| ||||
 .
| ||||
Импульсная функция 
соответствует решению однородного уравнения (5.10), когда 
, при следующих начальных условиях:
Приведенная масса и обобщенная сила для составных систем
Дадим расшифровку скалярных произведений, определяющих обобщенную силу и приведенную массу (5.10а) на примере механической системы, совершающей поперечные колебаний (рисунок 5.1). На рисунке 5.1 приняты обозначения:
F 1, F II, F IY, F 5 – сосредоточенные силы,
G III и G6 – сосредоточенные моменты,
вся балка разбита сосредоточенными элементами на шесть участков.
| F 1 |
| I |
| II |
| F II |
| III |
| GIII |
| F IY |
| F 5 |
| G6 |
| Y |
| m II |
| m III |
| m IY |
| m Y |
| J III |
| J Y |
Рисунок 5.1
Прежде чем перейти к обобщенной силе и приведенной массе всей системы, рассмотрим отдельно простейшие случаи.
1. Поперечные колебания стержня с погонной массой m и распределенной силой f (t, x) (рисунок 5.2).
В этом случае на основе обобщенного скалярного произведения получим:
Рисунок 5.2 |
|
2. На стержень дополнительно действует сосредоточенная сила Р (t), и к нему присоединена сосредоточенная масса М (рисунок 5.3).
Рисунок 5.3 | В этом случае путем использования обобщенной дельта-функции D(х) сосредо-точенные силу Р и массу М можно представить в виде распределенных параметров: | |||||||
| (5.18) | |||||||
Тогда с учетом свойств D – функции обобщенная сила и приведенная масса запишутся так:
| (5.19) |
|
3. На стержень действует сосредоточенный момент G, который можно представить в виде двух бесконечно близко расположенных сосредоточенных противоположно направленных сил (рисунок 5.4):
Рисунок 5.4 |
Тогда обобщенную силу запишем так:
|
Устремляя в формуле (5.21) e к нулю, придем к следующему значению обобщенной силы:
| (5.22) |
Отметим, что сосредоточенные силы и моменты могут быть также приложены к граничным точкам системы 0 и l. В этом случае обобщенные силы сохраняют вид (5.19) и (5.22), где вместо координат xР и xG нужно подставить соответственно 0 и l.
4. К стержню присоединены маятник и осциллятор, к которым приложены силы P I и P II (рисунок 5.5). По физическому смыслу произведение обобщенной силы на вариацию обобщенной координаты равно вариации элементарной работы внешней силы
| (5.23) | |||||
Рисунок 5.5
|
Элементарная работа сил (см. рис. 5) запишется так:
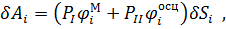
| (5.24) |
где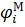 
и 
– абсолютные перемещения массы маятника и осциллятора, соответствующие i -му тону колебаний системы. Отсюда для обобщенной силы получим следующее выражение:
 .
| (5.25) |
Приведенная масса системы (см. рис. 5) имеет вид
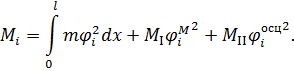
| (5.26) |
Это следует из структуры уравнений движения маятника и осциллятора.
5. Из анализа уравнений движения состыкованных стержней с различного рода инерционными включениями ясно, что вектор перемещений ji, входящий в скалярное произведение, компонуется из кинематических подвекторов (абсолютных перемещений и углов поворота) всех элементов системы, а матрица масс – в соответствии с видом инерционных членов, входящих в уравнения движения составных элементов системы. Из структуры формул для расчета приведенной массы (5.19), (5.26) видно, что они аналогичны формулам кинетической энергии (увеличенной вдвое), в которых для получения приведенной массы необходимо линейные и угловые скорости инерционных элементов заменить перемещениями и углами поворота соответствующих элементов по некоторому тону колебаний. Указанная аналогия позволяет упростить построение приведенной массы для любой сколь угодно сложной системы по известной форме колебаний и инерционным характеристикам системы.
Что касается обобщенной силы, то по определению произведение обобщенной силы на вариацию обобщенной координаты d si равно работе внешних силовых факторов на вариациях линейных и угловых перемещений, соответствующих i -й обобщенной координате d Ai = Fi d si. Отсюда следует, что если на стержневую систему (при поперечных колебаниях) действуют распределенные силы f (x, t), а также сосредоточенные силы и моменты Рn и Gk в сечениях хРn и хGk, то обобщенная сила примет вид
| (5.27) |
где ji и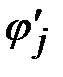 
– перемещения и углы поворота сечения по j- му тону колебаний.
6. После рассмотрения типовых элементов, дающих вклад в обобщенную силу и приведенную массу, и общего анализа физического содержания указанных величин вернемся к рассмотрению системы, изображенной на рисунке 5.1.
Приведенная масса указанной системы при поперечных колебаниях запишется так:
 .
| (5.28) |
Первое слагаемое соответствует вкладу в приведенную массу шести стержневых элементов, остальные слагаемые – вкладу маятника II, груза III, осциллятора IY и груза Y.
Обобщенная сила в том случае, если на каждый стержневой элемент, кроме указанных на рисунке 5.1 сил и моментов, будут действовать распределенные силы fk (x, t) (k = 1, 2,..., 6), запишется так:
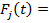
| (5.29) |
Здесь имеется в виду, что каждое внешнее силовое и моментное воздействие может изменяться во времени.