Вынужденные колебания ферм при вибрационной нагрузке
Канонические уравнения вынужденных колебаний ферм при вибрационной нагрузке P=P0sinθt аналогичнытем, которые были записаны для рам. Подставляя амплитудные значения инерционных сил 
, можно канонические уравнения представить в виде системы линейных алгебраических уравнений относительно неизвестных амплитудных значений инерционных сил Z1, Z2,…Zn:
(9.2.1)
Вводим следующие обозначения,
….. 
Тогда систему (9.2.1) можно переписать в упрощенном виде:
(9.2.2)
Для получения канонических уравнений в развернутом виде, надо к вырезанному узлу kприложить действующие вибрационные силы PkxsinθtиPkysinθt, а также инерционные силы, приложенные к массе (рис. 9.2.1):
Рисунок 9.2.1. Направления инерционных, продольных и внешних нагрузок в k-ом узле.
Уравнения динамического равновесия имеют вид:
(9.2.3)
Эти уравнения можно записать:
(9.2.4)
Определение динамического коэффициента.
Динамический коэффициентμот заданной гармонической нагрузки показывает,во сколько разее динамическое действие превышает статическое действие ее амплитуды. Динамический коэффициент определяют для изгибающего момента, поперечной силы и перемещения, т.е.
Т.к.динамический коэффициент больше 1, то учет сил инерции приводит к увеличению внутренних сил и деформаций. Для построения полной эпюры изгибающих моментов надо учесть так же влияние на изгиб вес массQ1, Q2, Q3и сложить с М дин.
3. На стальной раме из двутавра №24 находятся два груза с массами m=700кг и работающий двигатель с N=100 об/мин (рис. 3). Двигатель создает вибрационную нагрузку, максимальное значение которой 
=95 Н. Провести расчет рамы на воздействие вертикальной составляющей вибрационной нагрузки 
, считая грузы точечными. Собственным весом двигателя и стержней рамы пренебречь. Принять условно EI=1, a=300см
Рис. 3
Решение. Установим необходимые исходные данные: a=3 м; m=1000 кг; E=2,1×106 кг/см2 =2×1011 Н/м2; I=3460 см4=0,346×10-4 м4; EI=0,692×107 Нм2; W=289 см3=0,289×10-3 м3; [s]=1600 кг/см2=1,57×108 Н/м2; [s дин ]=1/4[s]=3,92× 107 Н/м2.
1. Расчет на собственные колебания
Если не учитывать продольные колебания стержней, то положение двух точечных масс данной рамы будет определяться двумя независимыми параметрами y 1, y 2 (рис. 4 а). Следовательно, число динамических степеней системы равно двум.
Рис. 4
Выберем положительные направления перемещений и обобщенных сил (рис. 4 а, б). В направлении первой степени свободы колеблются обе массы, а в направлении второй степени − только одна из масс. Поэтому 
и матрица масс системы будет
.
Дляопределенияматрицы податливости d рассмотрим два единичных загружения системы (рис. 4 в, г) и в каждом из них построим эпюры изгибающих моментов. Данная рама статически неопределима, поэтому ее статическую неопределимость раскроем методом сил, как более выгодному в этом случае (n мс = 
3=4−3=1, nмп= n угл+ n лин= 2+2=4).
На рис. 5 представлены основная система (рис. 5 а), единичная эпюра 
(рис. 5 б) и грузовая эпюра 
(рис. 5 в) для первого единичного состояния.
Каноническое уравнение метода сил будет 
, а его коэффициент 
и свободный член 
.
Рис. 5
Тогда 
. По формуле 
строим эпюру моментов для первого единичного состояния (рис. 6 а).
Аналогично строится эпюра второго единичного состояния (рис. 6 б).
Рис. 6
Вычислим элементы матрицы податливости 
. В статически неопределимой системе их можно вычислить двумя способами: 1) 
или 2) 
. Второй способ проще:
.
Аналогично, 
.
Величину последнего элемента найдем первым способом:
.
Тогда 
, 
.
Если ввести обозначение 
, то матричное уравнение собственных колебаний 
принимает вид
. (1)
Из векового уравнения 
получим полином
,
который имеет два корня 
, 
.
Определим собственные значения и соответствующие им круговые частоты собственных колебаний:
; 
;
; 
.
Для определения форм собственных колебаний систему уравнений (1) запишем в обычном виде:
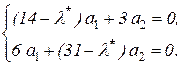
Если положить a 1= 1 и исключить первое уравнение, то второе уравнение будет
,
откуда
.
Из этого уравнения определяются ординаты форм собственных колебаний:
– для первой формы при 
имеем 
, 
;
– для второй формы при 
= 13 имеем 
, 
.
Эти формы удовлетворяют условию ортогональности:
.
Представим обе формы колебаний графически (рис. 7 а, б):
Рис. 7
2. Проверка на резонанс
Определим круговую частоту вибрационной силы:
.
Тогда
;
.
Как видно, близко резонансное состояние по 1-ой форме. Следовательно, расчеты необходимо продолжить.
3. Проверка динамической прочности
С этой целью проведем расчет на вынужденные колебания. Вначале определим вектор амплитудных значений вибрационной нагрузки:
.
Запишем канонические уравнения расчета на вибрационную нагрузку
и вычислим их коэффициенты:
;
;
.
Определим правые части уравнений:
.
Тогда 
, 
.
Система канонических уравнений принимает вид
из которой получаем: J 1= 264, J 2 = 718.
Определим обобщенные силы:
;
.
Они показаны на рис. 8 а.
По формуле 
строим эпюру наибольших динамических моментов (рис. 8 б). Из нее определяем: 
.
Таким образом, условие прочности выполняется.
Рис. 8
4. Проверка динамической жесткости
Техническая частота вращения двигателя: 
Гц.
Максимальные перемещения масс при колебаниях:
,
.
На рис. 8 впоказана примерная форма колебаний рамы. Как и следовало ожидать (так как частота нагрузки близка к первой форме), она близка к первой форме собственных колебаний.
Из табл. 1 следует, что если человек во время работы будет постоянно находиться рядом со 2-ой массой, то амплитуда колебаний будет превышать допустимую (при частоте f=3,33 Гц амплитуда a ≈ 1 мм). Поэтому жесткость рамы недостаточна и ее необходимо укрепить.