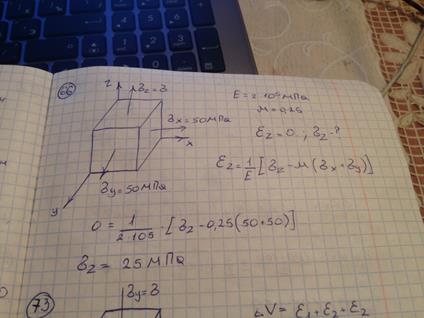
80) Объемный элемент находится под действием нормальных напряжений, показанных на рисунке: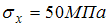 
, 
, 
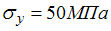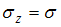. Модуль упругости материала 
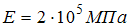, коэффициент Пуассона 
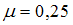. Линейная деформация в направлении оси z будет равна нулю, когда 
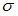принимает значение 25Мпа.
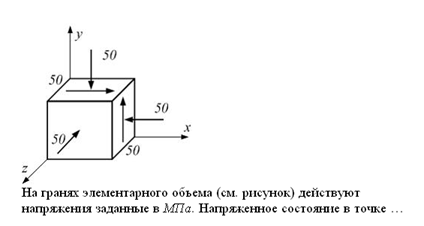
81) На гранях элементарного объёма действуют напряжения, заданные в Мпа. Напряженное состояние в точке где только одно нормальное напряжение.(Линейная деформация) (Сжатие)
82) Изотропный материал на растяжение и сжатие работает неодинаково. Для оценки прочности материала при сложном напряженном состоянии используется теория О. Мора.
При оценке прочности материала, неодинаково работающего на растяжение и сжатие, используют теорию прочности О. Мора. Эквивалентное напряжение по данной теории определяют по формуле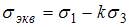 
.
Коэффициент «k » для пластичного материала равен отношению предела текучести при растяжении к пределу текучести при сжатии,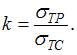 
Для хрупкого материала 
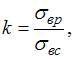где 
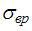– предел прочности материала при растяжении, 
– предел прочности материала при сжатии.
83) Площадки в исследуемой точке напряженного тела, на которых касательные напряжения равны нулю, называют главными, а нормальные напряжения, действующие по этим площадкам, называются главными напряжениями.
84) Напряженное состояние при значениях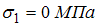 
, 
, 
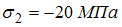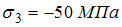называют плоским.
85) Три взаимно перпендикулярные оси, в системе которых отсутствуют угловые деформации, называют главными осями деформированного состояния. Среди множества осей, проходящих через точку, в которой исследуется деформированное состояние, существуют три взаимно перпендикулярные оси, в системе которых угловые деформации равны нулю. Эти оси называются главными осями деформированного состояния, а линейные деформации в этой системе – главными деформациями.
|
|
86) Совокупность линейных и угловых деформаций, возникающих по раз-личным осям и в различных плоскостях, проходящих через данную точку тела, называют деформированным состоянием в точке.
В общем случае элементарный объем испытывает три линейные деформации и три угловые. Деформированное состояние в точке полностью определяется, если заданы шесть компонентов тензора деформаций (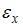
, 
, 
, 
, 
, 
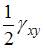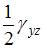). Зная эти компоненты, можно определить линейную и угловую деформации в любом направлении и в любой плоскости, проходящей через данную точку. Совокупность этих деформаций по множеству направлений и плоскостей, проходящих через данную точку, и называется деформированным состоянием в этой точке.
87) Модуль упругости материала E и коэффициент Пуассона M заданы. Относительное изменение объёма равно
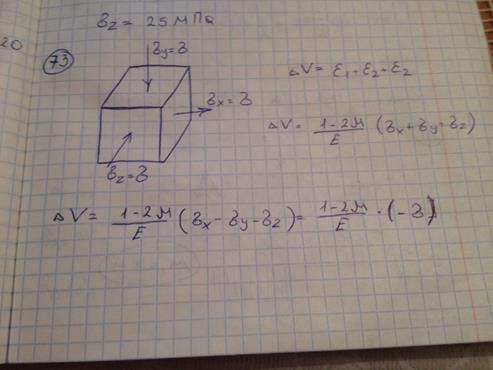
88) Главные напряжения для напряженного состояния, показанного на рисунке, равны
89) Зависимость между компонентами напряженного и деформированного состояния в пределах малых упругих деформаций носит название обобщенного закона Гука.
90) Согласно теории наибольших касательных напряжений (третья теория прочности), самое опасное напряженное состояние показано на рисунке ответ Б.
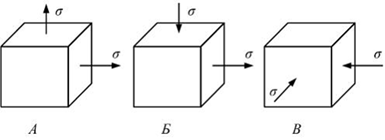
91) Тип напряженного состояния, показанного на рисунке, называется растяжение.
92) Чему равно наибольшее касательное напряжение в случае плоского напряженного состояния?
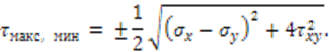
93) Что представляют собой площадки сдвига и как они наклонены к главным площадкам?
94) Проверка на прочность по касательным напряжениям необходима в случае, если длинные балки нагружены сосредоточенными силами и моментами.
|
|
95) Эпюра изгибающих моментов имеет вид:
96) Балка нагружена равномерно распределенной нагрузкой интенсивности q. Эпюра изгибающих моментов имеет вид…
97) Вывод формулы для определения нормальных напряжений при чистом изгибе основывается на гипотезе плоских сечений и гипотезе об отсутствии взаимного надавливания продольных слоев балки.В основе гипотезы плоских сечений лежит предположение, что и внутри стержня деформации имеют такой же характер, как на поверхности.
98) Прямоугольная балка имеет два варианта расположения поперечного сечения. Отношение наибольших нормальных напряжений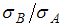 
для этих двух вариантов равно ответ 2.
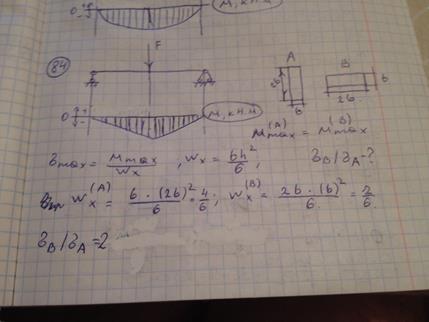
99) Консольная балка нагружена, как показано на схеме. Материал балки одинаково работает на растяжение и сжатие. Допускаемое напряжение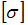 
, размеры b и l заданы. Из расчета по допускаемым напряжениям значение силы
100) Стальная балка имеет два варианта расположения квадратного поперечного сечения. В первом случае она нагружается параллельно стороне квадрата. Во втором – в диагональной плоскости. Отношение прогибов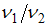 
равно
101) Из таблицы сортаментов для двутавровых балок имеем:
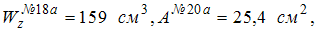
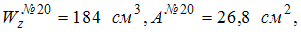
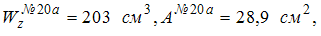
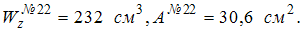
В опасном сечении балки, выполненной из пластичного материала (допускаемое напряжение [s] = 160 МПа), значение изгибающего момента 
. Отношение массы балки прямоугольного сечения (с отношением сторон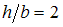 
) к массе балки двутаврого сечения равно ответ: 3.1.
102) Полная проверка прочности балки при изгибе включает в себя проверку по нормальным напряжениям, проверку по касательным напряжениям и проверку по главным напряжениям.
|
|
103) Прогиб на свободном конце балки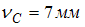 
. Угол поворота поперечного сечения над опорой 
равен 24 минуты.
104) Поперечная сила Qy в произвольном поперечном сечении стержня численно равна алгебраической сумме проекций на ось y всех внешних сил (в том числе и реакций внешних связей), расположенных по одну сторону от рассматриваемого сечения.
105) При плоском поперечном изгибе нормальные напряжения по ширине сечения балки распределяются равномерно.
106) Консольная балка на участке АВ нагружена равномерно распределенной нагрузкой интенсивности q. Жесткость поперечного сечения стержня на изгиб EIz всей длине постоянна. Угол поворота сечения B, по абсолютной величине равен
107) Жесткость поперечного сечения на изгиб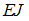 
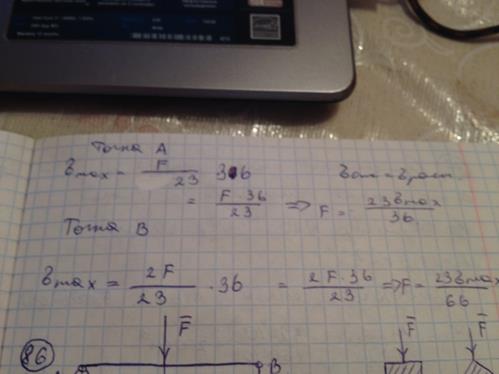
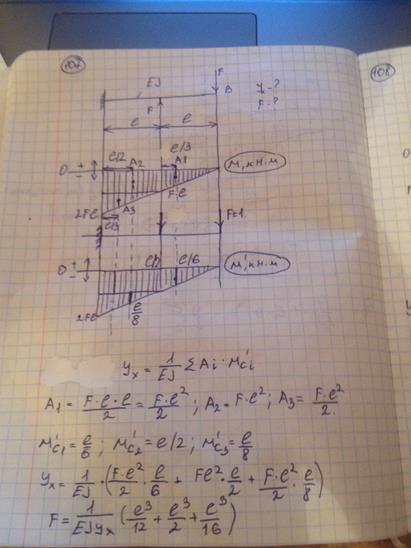
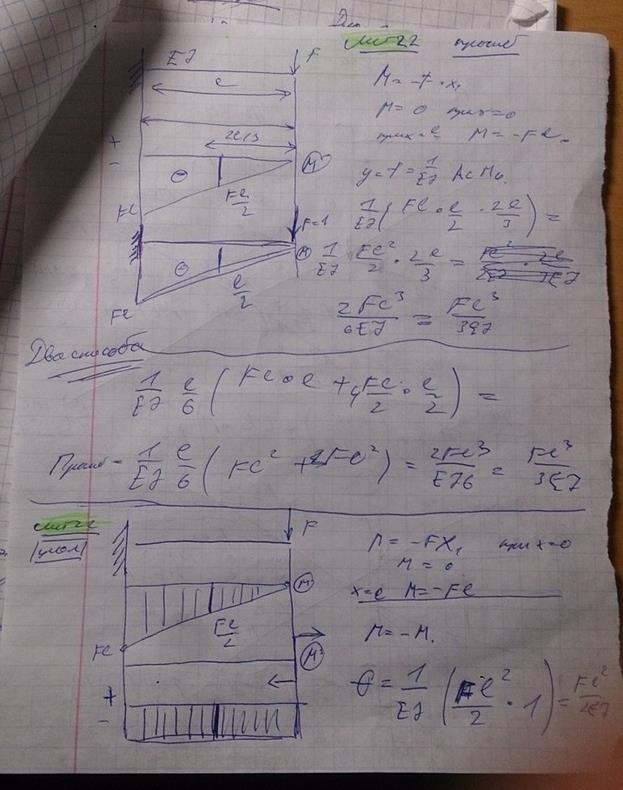
по длине балки постоянна. Размер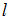 
задан. Значение силы F, при которой прогиб концевого сечения В будет f, равно
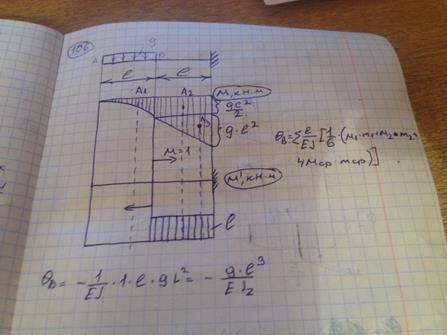
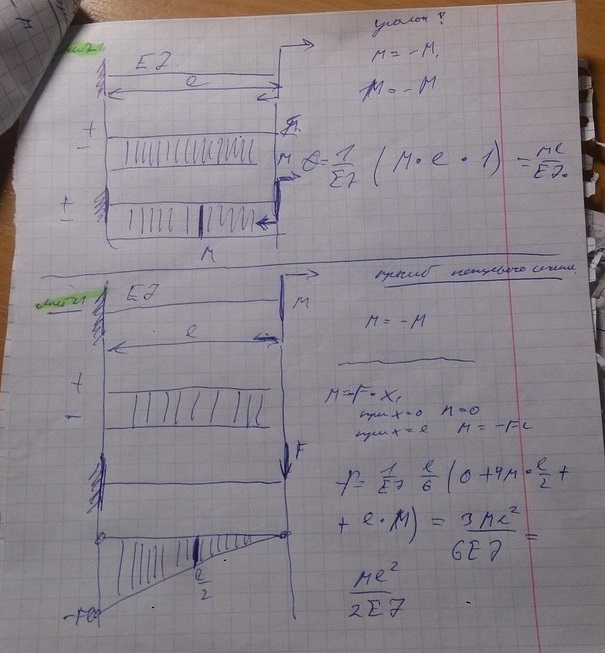
108) Жесткость поперечного сечения на изгиб 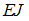по длине балки постоянна. Сила F, размер l заданы. Прогиб свободного конца балки равен нулю, когда значение момента M равно
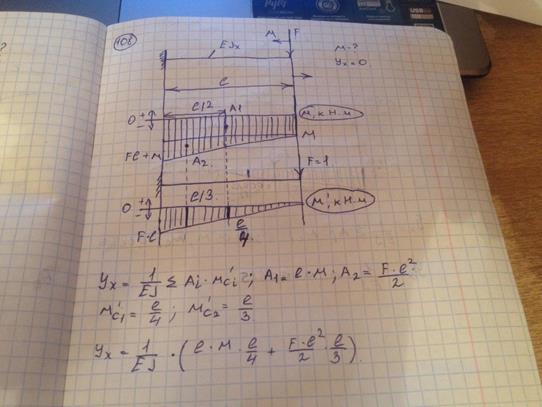
109) Для вычисления интегралов Мора использовать правило Верещагина. Вертикальное перемещение сечения C равно
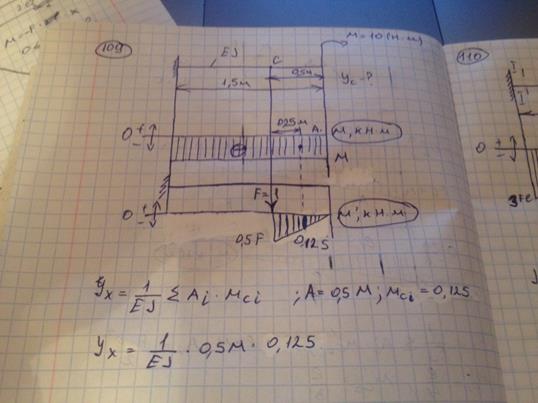
110) Схема нагружения балки прямоугольного сечения с размерами bx3b представлена на рисунке. Сила F и размер l заданы. Значение нормального напряжения в точке K сечения I-I равно
111) Степень статической неопределимости для плоского замкнутого контура равна 3. В поперечном сечении плоского замкну-того контура имеют место три внутренние связи. Они запрещают взаимные два линейных перемещения и одно угловое двух сторон сечения.
112) Что такое момент сопротивления при изгибе и какова его раз-мерность? Способность тела сопротивляться изгибу, ед. измерения см^3.
113) По какой формуле определяются касательные напряжения при поперечном изгибе?
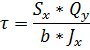
114) Для заданной статически неопределимой балки пред-ставлены четыре варианта основной системы метода сил. Неправильный ответ соответствует варианту 4.
Данная балка является два раза статически неопределимой системой. На нее наложены шесть связей (необходимых четыре). Таким образом, дополнительных связей две. Удаление двух связей (удаление опоры В и превращение жесткой заделки в шарнирно-неподвижную опору) превращает систему в кинематически изменяемую.
115) Система канонических уравнений имеет вид 
. Произведение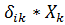 
– это перемещение по направлению i-го силового фактора от неизвестной k-ой силы.
На основании принципа независимости действия сил перемещение в направлении i -ой неизвестной силы равно сумме перемещений от действия всех неизвестных сил, внешней нагрузки и равно нулю, т.е.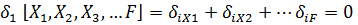 
.Каждое пе-ремещение пропорционально соответствующей силе, поэтому величину 
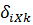можно записать в виде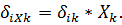 
116) В чем заключается проверка эпюр Q и M при изгибе?
Статическая проверка правильности эпюр Q и M заключается в составлении условий статического равновесия всей системы в целом, ее узлов и отдельно выделенных произвольных частей.
117) На каком волокне поперечного сечения балки изображается эпюра изгибающих моментов? На сжатом волокне.
118) Как расположены нейтральный слой и нейтральная ось при поперечном изгибе? По середине поперечного сечения балки.
119) По какой формуле определяются нормальные напряжения в поперечном сечении балки при поперечном изгибе и как они изменяются по высоте балки?
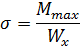
120) Что называется жесткостью сечения при изгибе? Способность конструкции сопротивляться изгибу при внешнем воздействии.
121) Определить угол поворота сечения балки над левой опорой
122) Определить угол поворота сечения балки над правой опорой
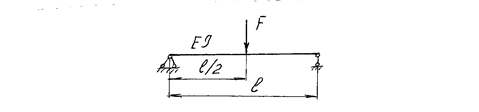
123) Определить стрелу прогиба балки
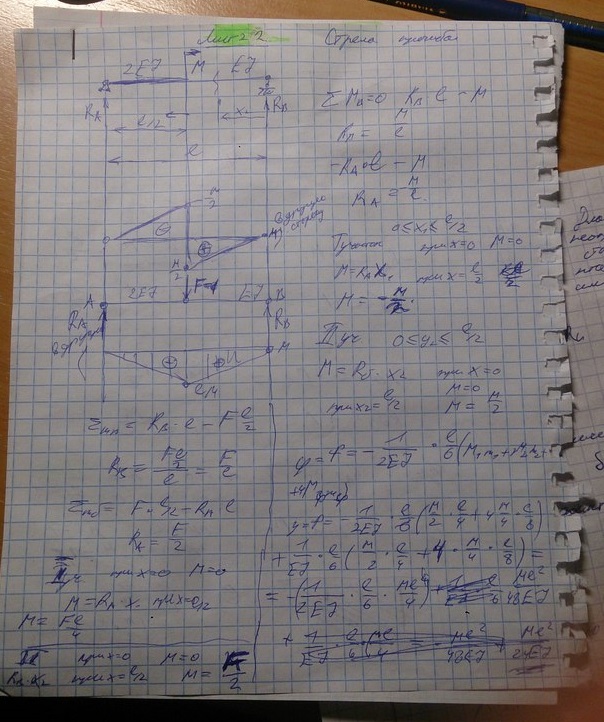
124) Определить прогиб концевого сечения балки. Определить угол поворота концевого сечения балки.
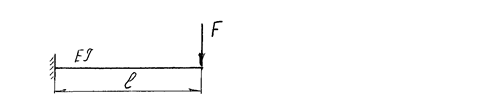
125) Определить стрелу прогиба балки
126) Определить угол поворота сечения балки над правой опорой
127) Определить угол поворота концевого сечения балки
128) Балка нагружена равномерно распределённой нагрузкой интенсивности q. Жесткость поперечного сечения балки на изгиб по всей длине постоянна и равна EJ. Прогиб в середине пролета балки длиной l равен
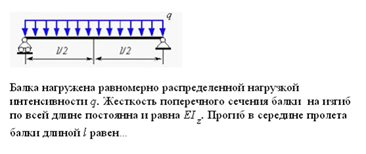
129) Определить угол поворота сечения балки над левой опорой