Симметричный оптимум
Рассмотрим сначала структурную схему двигателя постоянного тока при питании от тиристорного преобразователя (рис.10.18).
Если считать управляющее воздействие постоянным, то изменение (перепад) скорости 
в установившемся режиме может быть установлено с помощью выражения:
, (1)
где
–
передаточная функция двигателя постоянного тока по возмущающему воздействию.
Если считать, что нагрузка изменяется скачком и является постоянной по величине (рис.10.19), то
.
Используя теорему о конечном значении (табл.2.2), получаем:
. (2)
С учетом (1) получаем, что статическое падение скорости (по модулю)
. (3)
Рассмотрим теперь систему регулирования скорости с пропорциональным РС (рис.10.20).
Контур регулирования тока (КРТ) аппроксимирован апериодическим звеном с передаточной функцией
.
Пусть контур регулирования скорости (КРС) синтезирован по модульному оптимуму:
; 
.
Система регулирования скорости с пропорциональным РС является однократноинтегрирующей: астатической 1-го порядка по управлению и статической по отношению к нагрузке 
(величина установившейся скорости 
зависит от нагрузки). Передаточная функция замкнутой системы регулирования скорости по возмущению:
(4)
Статическое падение скорости (по модулю):
. (5)
Если сравнить это выражение с аналогичным выражением для двигателя постоянного тока (разомкнутой системы) – то есть, сравнить (3) и (5), – то получим соотношение:
. (6)
Таким образом, статическое падение скорости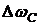 
в замкнутой системе равно статическому падению скорости в разомкнутой системе, помноженному на 
. В реальных системах:
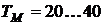мс;
мс.
Поэтому в замкнутых системах статическое падение скорости оказывается в 1,0…3,5 раза меньше.
Дополним рассмотренную систему регулирования скорости еще одним КРС с интегральным РС, используя тот же сигнал обратной связи (на рис.10.20 соответствующие линии показаны пунктиром).
Из условия оптимизации по модульному оптимуму:
,
что даст
; 
%.
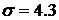Рассмотрим левую часть системы (рис.10.20), и первую обратную связь по скорости (сплошная линия) перенесем на вход интегрального РС (рис.10.21).
Формировать дифференцирующее звено в канале ОС по скорости нецелесообразно (поскольку сложно и не следует усиливать помехи, которые обязательно присутствуют). Поэтому преобразуем схему рис.10.21 путем переноса точки приложения задания UωЗ в точку а.
В результате получим структурную схему, приведенную на рис.10.22. Правая часть структурной схемы СПР скорости остается без изменений (см. рис.10.20). Таким образом, СПР с двумя (П- и И-) регуляторами скорости эквивалентна системе с фильтром Ф на входе и пропорционально-интегральным (ПИ-) регулятором скорости.
СПР скорости с ПИ-РС является астатической 2-го порядка по возмущению и астатической 1-го порядка по управлению. Поскольку ПИ-РС фактически содержит два интегратора (один из них скомпенсирован дифференциатором, введенным для компенсации интегратора в механической части объекта), ее часто называют двукратноинтегрирующей СПР скорости.
Передаточная функция разомкнутого КРС:
,
где ; 
.
Используем правило оперативного определения частоты среза:
· после 1-го этапа: 
.
· после 2-го этапа: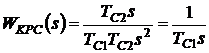 
.
· после 3-го этапа: 
, откуда 
.
ЛАЧХ разомкнутого КРС приведена на рис.10.23.
Таким образом, ЛАЧХ оказывается симметричной относительно частоты среза 
: ЛАЧХ имеет наклон "–2–1–2", частота располагается строго посредине частот сопряжения, которые отличаются друг от друга в 4 раза.
Учитывая вид ЛАЧХ, такую настройку КРС, когда внутренний КРТ аппроксимируется апериодическим звеном с постоянной времени 
, а регулятор скорости выбирается ПИ-типа, часто называют настройкой на симметричный оптимум.
При наличии фильтра на входе системы переходная функция КРС 
имеет перерегулирование 
, и время первого согласования 
. В этом случае система воспроизводит линейно нарастающий сигнал 
с установившейся ошибкой 
.
Примечание. Коэффициент 
датчика скорости используется в сигнале задания как масштабный коэффициент: на узел сравнения должны прийти сигналы (задания и обратной связи) одного порядка.
При отсутствии фильтра на входе значения показателей качества переходных процессов составят 
, 
(если КРТ синтезирован таким образом, что он представляет собой колебательное звено с 
), и 
(если КРТ представлен апериодическим звеном с постоянной времени ). В этом случае ошибка при отработке линейного управляющего воздействия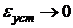 
.
Поскольку сам КРС (без фильтра на входе) воспроизводит линейно изменяющийся сигнал без ошибки, то эта ошибка воспроизведения управляющего сигнала обусловлена именно ошибкой воспроизведения фильтром входного сигнала (рис.10.24):
Используя теорему о конечном значении:
