Кафедра прикладной математики
Название работы:
лабораторная работа на тему
Нахождение корня уравнения
-методом деления отрезка пополам;
-методом Ньютона;
-методом хорд;
ОТЧЕТ
| Студент _______ | Якушова Е.Ю. | |
| (подпись, дата) | (инициалы, фамилия) | |
| Группа М2-С-09 | ||
| (шифр группы) | ||
| Руководитель | ||
| Преподаватель | __________ | Чепурко С.В. |
| (ученая степень, звание) | (подпись, дата) | (инициалы, фамилия) |
Обнинск,2012
CОДЕРЖАНИЕ:
1 МЕТОД ДЕЛЕНИЯ ОТРЕЗКА ПОПОЛАМ………………………………2
1.1 Постановка задачи………………………………………………….2-3
1.2 Достоинства и недостатки метода…………………………………3
1.3 Код программы…………………………………………………………4
1.4 Результаты программы………………………………………………..5
2 МЕТОД ХОРД
2.1 Постановка задачи………………………………………………..…..…6-7
2.2 Код программы……………………..……………………………………..7
2.3 Результаты программы………………………………..…………………8
3 МЕТОД НЬЮТОНА
3.1 Постановка задачи…………………………………………………...9-10
3.2 Код программы…………………………………………………………..11
3.3 Результаты программы…………………………………………………12
МЕТОД ДЕЛЕНИЯ ОТРЕЗКА ПОПОЛАМ
1.1 Постановка задачи:
Ур-е:f(x)=0,xє[a,b] (1)
f(x)-непрерывна на [a,b]
f(a)*f(b)<0 (2)
Функция имеет хотя бы 1 точку пересечения с осью Ох,т е имеет корень.
Алгаритм:а0=а, b0=b, c0=(a0+b0)/2;
Отрезок [a,b] разбивается на [a0,c0],[c0,b0].Из этих ввух отрезков выбираем тот,у которого значение ф-ии на концах имеет разные знаки и выбранный отрезок переобозначаем [a1,b1].
[a0,c0] [c0,bo]->[a1,b1]
If (f(c0)=0) x*=c0;иначе продолжаем процедуру.
Проверяем f(a1)f(b1)<0;[a1,b1] делим пополам;выбираем нужный отрезок,ф-я на краях которого имеет разные знак и так далее.
В результате имеем последовательность вложенных друг в друга отрезков[a0,b0] [a1,b1]…[an,bn]…таких что f(an)f(bn)<0,n>1;
bn-an=(b0-a0)/2^n; (3) (т к при каждом делении длина отрезка уменьшается вдвое)
Теорема(о сходимости метода деления отрезка пополам)
Пусть f(x) непрерывна на [a,b] и f(a)*f(b)<0.Тогда последовательности an и bn сходятся к корню уравнения (1).
Док-во:an:a1,a2,..,an-последовательность левых краев вложенных друг в друга отрезков.По построению она монотонно неубывает ограничена сверху(b).=>X= 
bn:b1,b2,..,bn-последовательность правых краев вложенных друг в друга отрезков.По построению она монотонно невозрастает ограничена снизу(а).=>X= 
Возьмем операцию предела от (3) 
=0=>X=X+=x*
Покажем что х*-корень ур-я(1).Возьмем опрерациб предела от(2)
=f()f()= 
(x*)<=0(2).Т е квадрат ф-ии <=0,следовательно,единственный допустимый случай f(x*)=0;
ч т д
1.2 Достоинства и недостатки метода:
+)Сходится всегда.
-)Сходится быстро,если корней несколько,то при неверном отделении –неправильность в выборе корня
1.3 Код программы:
#include <iostream>
#include <math.h>
#include <conio.h>
using namespace std;
double e, a, b;
double f(double x)
{return sin(x)+cos(x)-pow(x,0.5);}
void delenie ()
{double c=(a+b)/2;
int k=0;
while (fabs(f(c))>=e)
{c = (a + b)/2;
if (f(a)*f(c)<0) b=c;
else
a=c;
k++;
}
cout << "x* = " << c <<endl;
cout << "iter= " << k<<endl;
}
void main()
{ cout << "input a"<<endl;
cin >> a;
cout << "input b"<<endl;
cin >> b;
cout << "input eps"<<endl;
cin >> e;
if(f(a)*f(b)>0) cout<<"error"<<endl;else
if(a<0||b<0) cout<<"error"<<endl;else
if(a==b)cout<<"error"<<endl;
else delenie();
getch();
;
}
1.4 Результаты программы:
График ф-ии:
Нахождение корня ур-я и подсчет кол-ва итераций в зависимости от задания промежутка рассмотрения [a,b] и точности eps.
a=0 b=3 eps=0.001 x*=1.376953125 i=9
a=1 b=1 eps=0.1 x*=1.375 i=3
a=1 b=10 eps=0.00001 x*=1.37732287268 i=19
a=-3 b=-7 eps=0.001 x-error i=error
a=4 b=6 eps=0.001 x-error i=error
a=1.2 b=1.7 eps=0.0001 x=1.377368164 i=12
МЕТОД ХОРД
2.1 Постановка задачи:
f(x)=0, xє[a,b] (1)
f(x)-непрерывна;
f(a)*f(b)<0;
[a,b]->[a,c] [c,b].Из этих двух отрезков выбираем тот у которого ф-я на концах имеет разные знаки.
Найдем формулу,по которой высисляется с:
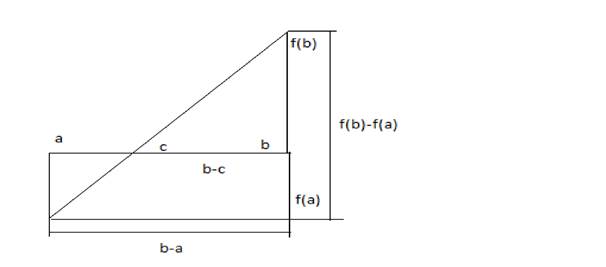
Из соотношения подобия имеем: 
= 
=>c находим как 
= 
=> 
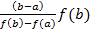1.2 Код программы:
#include <iostream>
#include <math.h>
#include <conio.h>
using namespace std;
double e, a, b;
double f(double x)
{return sin(x)+cos(x)-pow(x,0.5);}
void horda ()
{double c=b-(b-a)*f(b)/(f(b)-f(a));
int k=0;
while (fabs(f(c))>=e)
{ c=b-((b-a)*f(b)/(f(b)-f(a)));
if (f(a)*f(c)<0) b=c;
else
a=c;
k++;
}
cout << "x* = " << c <<endl;
cout << "iter= " << k<<endl;
}
void main()
{ cout << "input a"<<endl;
cin >> a;
cout << "input b"<<endl;
cin >> b;
cout << "input eps"<<endl;
cin >> e;
if(f(a)*f(b)>0) cout<<"error"<<endl;else
if(a<0||b<0) cout<<"error"<<endl;else
if(a==b)cout<<"error"<<endl;
else horda();
getch();
;
}
2.3 Результаты программы:
График аналогичен графику из предыдущего метода.
Нахождение корня ур-я и подсчет кол-ва итераций в зависимости от задания промежутка рассмотрения [a,b] и точности eps.
a=0 b=10 eps=0.01 x*=1.371693772 i=9
a=1 b=3 eps=0.0001 x*=1.3773131424 i=7
a=-1 b=3 eps=0.00001 x-error i-error
a=-1 b=0 eps=0.001 x*-error i-error
a=4 b=6 eps=0.001 x*-error i-error
a=1 b=6 eps=0.000001 x*=1.377336696 i=12
МЕТОД НЬЮТОНА
3.1 Постановка задачи:
f(x)=0,f(x) непрерывна на [a,b]; (1)
f(a)*f(b)<0;
x=x+ 
, x=x- 
, 
- 
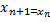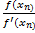, n=0,1,2…
x*:f(x*)=0;
Пусть известно некоторое значение 
, тогда f(x*)=f(x*+ - )=0.Раскладываем по ф-ле Тейлора и устремляем к 0 f”(
тогда x* 
x 
. Заменяем на = и имеем слева приближенное значение 
= -
Геометрический смысл:
Tg 
=f’(x0)=f(x0)/x0-x1 => x1=x0 - 
; касательными приближаемся к корню.
Теорема(о сходимости метода Ньютона):
Пусть ф-я f(x) дважды непрерывно дифференцируема на [a,b]. И f(a)f(b)<0;
f’ f” знакопостоянны на [a,b].Тогда итерационный процесс уравнения Ньютона сходится к единственному корню уравнения f(x)=0;
И для погрешности справедлива формула |x*- | 
M2/2m1*( - 
), где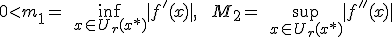 
,
Док-во:
Для определенности f(a)<0, f(b)<0, f’(x)>0,f’’(x)>0;
Рассмотрим итерационный процесс и покажем что 
>x*;
Пусть f’(x)>0, f’’(x0)>0. Тогда в качестве x0 берем точку x0=b, так как f(b)f’’(b)>0. Из (3.23) следует, что xn+1<xn, то есть последовательность {xn} является убывающей
b=x0>x1>…>xn>a (3.24)
Покажем теперь, что эта последовательность имеет предел ξ. Пусть xn-1> ξ. Докажем, что xn> ξ. Для этого запишем n-ое приближение, полученное по формуле Ньютона (см. формулу (3.17)) и по модифицированной формуле Ньютона (3.23)
= 
- 
= -
и найдем разность - = 
*(
)
. (3.25)
Из теории выпуклых функций известно, что если f’’(x) и сохраняет знак на [a,b], то f(x)является выпуклой. Для выпуклой функции f(x) производная f’(x) является неубывающей, то есть для любого x2>x1,f’(x2) 
. Поэтому f’() 
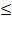f’(
)
. 
(3.26)
С учетом (3.26) из (11) следует ^x- 
. Из теоремы сходимости метода Ньютона мы получали ^ 
, поэтому 
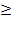кси Отсюда
ξ≤xn. (3.27)
Таким образом, из (3.24) и (3.27) получили убывающую сходящуюся последовательность
x0>x1>…>xn≥ξ.
Следовательно, для любого сколь угодно малого ε>0 можно указать такое n, что
|xn-ξ|< ε. Теорема доказана.
3.2 Код программы:
#include <iostream>
#include <cmath>
#include <conio.h>
using namespace std;
double f(double x)
{return(sin(x)+cos(x)-pow(x,0.5));}
double df(double x)
{return (-1/(2*pow(x,0.5))+cos(x)-sin(x));}
double ddf(double x)
{return (-sin(x)-cos(x)+1/(4*pow(x,1.5)));}
void main()
{
double x0,xn, e=0.0001, n=0, a, b;
cout<<"Vvedi a=";
cin>>a;
cout<<endl<<"Vvedi b=";
cin>>b;
cout<<"Vvedi x0=";
cin>>x0;
if(a<0||b<0)cout <<"error"<<endl;else
if(x0<0) cout <<"error"<<endl;else
if(a==b)cout <<"error"<<endl;else
if(f(a)*f(b)>=0)cout <<"error"<<endl;else
{if(f(x0)*ddf(x0)<=0) cout<<"error x0!"<<endl; else
{xn=x0-f(x0)/df(x0);
while(fabs(xn-x0)>=e){x0=xn;xn=x0-f(x0)/df(x0);n++;}
}cout<<n<<endl;cout<<xn;}
getch();
}
3.3 Результаты программы:
График аналогичен графику из предыдущих двух методов.
Нахождение корня ур-я и подсчет кол-ва итераций в зависимости от задания промежутка рассмотрения [a,b],точности eps и начального задания х0
.
a=1, b=7, x0=1.6, e=0.0001, i=3, x*=1.37734
a=2, b=4, x0=1.6 e=0.0001, i-error, x*-error
a=1,b=2, x0=1.7, e=0.0001, i=3, x*=1.3773369
a=1.1, b=2, x0=1.8,e=0.00001, i=5, x*=1.3773371