Лабораторная работа №6
Тема. Численные методы решения систем линейных алгебраических уравнений (СЛАУ).
Эта работа включает 4 задания. Для расчета используйте СЛАУ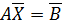 
из приложения 3 в соответствии с вариантом.
Задание 3.1. Решить систему линейных алгебраических уравнений методом Гаусса (точный метод).
Задание 3.2. Используя надстройку Excel поиск решения, решите СЛАУ, заданную вариантом.
Задание 3.3. Решите СЛАУ итерационным методом Якоби с заданной точностью e. Проанализируйте сходимость итерационного процесса в зависимости от e=0,1;. 0,01;.. 0,001.
Задание 3.4. Проанализировать корректность задачи (существование, единственность, устойчивость решения относительно исходных данных).
Порядок выполнения
1. Решите СЛАУ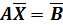 
методом Гаусса ( вручную):
· прямой ход: приведите СЛАУ к эквивалентной системе с треугольной матрицей А, т.е.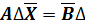 
· обратный ход: последовательно вычислите неизвестные x1,.x2,,хn
Пример 3.1. Решите СЛАУ (3.1) используя алгоритм метода Гаусса, приведенный на рис.3.1. Предварительно убедитесь, что система не является вырожденной.
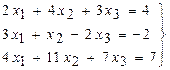(3.1)
Рис 3.1.Расчетная схема метода Гаусса
Как видно из рис 3.1, решением системы (3.1) является вектор
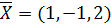
Задание 3.2. Используя надстройку Excel поиск решения, решите СЛАУ, заданную вариантом.
В приложении MS Excel имеется возможность решения СЛАУ с помощью надстройки «Поиск решения».
При этом приложение использует итерационные методы, т.е. строится последовательность приближений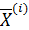 
, i=0,1,…n, i – номер итерации. Назовем вектором невязок следующий вектор:
Задача Excel заключается в том, чтобы найти такое приближение 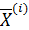, при котором вектор невязок стал бы нулевым, т.е. добиться совпадения значений правых и левых частей системы.
Последовательность действий:
Последовательность действий рассмотрим на примере СЛАУ (3.3):
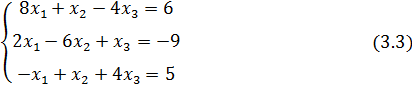
1. Оформите таблицу для решения СЛАУ (3.3), как показано на рис.3.2.
2. В ячейках А8:С8 будет сформировано решение системы (х1, х2, х3 ). Первоначально они остаются пустыми, т.е. равными нулю. Однако для контроля правильности вводимых далее формул, удобно ввести в эти ячейки какие-либо значения, например единицы. Эти значения можно рассматривать как нулевое приближение решения системы, т.е.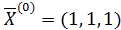 
.
3. Введите коэффициенты системы (матрицу А) в ячейки А3:С5.
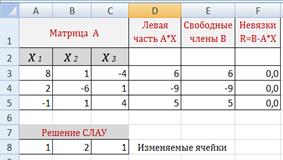
Рис 3.2. Решение СЛАУ с помощью надстройки
4. В столбец D введите выражения для вычисления левых частей исходной системы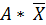 
. Для этого используйте функцию СУММПРОИЗВ из категории Математические.
5. В столбец Е запишите значения правых частей системы (матрицу В).
6. В столбец F введите невязки в соответствии с формулой (3.2). Будет не лишним проверить правильность вычислений для случая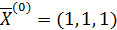 
.
7. Далее используйте надстройку Поиск решения, для этого:
· Выберите команду:
Данные\Анализ «что-если»\Поиск решения (рис. 3.3).
· В поле Изменяя ячейки укажите блок ячеек $А$8:$С$8,
· В поле Ограничения – $F$3:$F$5=0. Для этого надо щелкнуть на кнопке Добавить и ввести эти ограничения.
· Щелкните на кнопке Выполнить
Решение системы (3.3) получено в ячейках А8:С8 - х1=1; х2=2 х3=1 (рис.3.3)
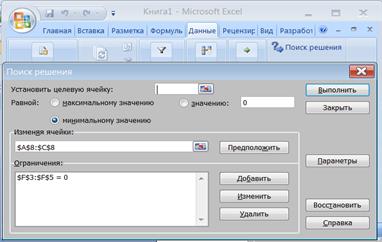
Рис.3.3. Окно Поиск решения
Задание 3.3. Решите СЛАУ итерационным методом Якоби с заданной точностью e. Проанализируйте сходимость итерационного процесса в зависимости от e=0,1;. 0,01;.. 0,001.
Порядок выполнения
1. Для расчета используйте СЛАУ в соответствии с вариантом.
2. Решите СЛАУ методом Якоби. Проанализируйте сходимость итерационного процесса.
3. Если итерационный процесс оказался расходящимся, преобразуйте исходную систему к виду, пригодному для построения итерационного процесса, т.е. к системе с «преобладанием диагональных элементов» матрицы системы.
4. Проверьте правильность сделанных преобразований, решив преобразованную СЛАУ с использованием надстройки Поиск решения.
5. Решите вручную систему методом Якоби, вычислив три итерации. В качестве начального приближения возьмите нулевой вектор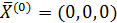 
. Сделайте вывод о продолжении или прекращении итерационного процесса для e=0,1.
6. Решите систему методам Якоби с точностью e=0,01, используя приложение Excel. Расчетная схема приведена на рис.3.4.
7. Исследовательская часть (численный эксперимент). Проанализируйте характер полученных решений для различных значений e =0,1; 0,01; 0,001, построив диаграмму n=n(ε).
8. Проанализируйте сходимость итерационного процесса, построив графики изменения каждой компоненты решения в зависимости от номера итерации (рис.3.5 или рис.3.6).
Пример решение СЛАУ методом Якоби
Пример 3.2.
Найти решение СЛАУ(3.3) методом Якоби с заданной точностью.
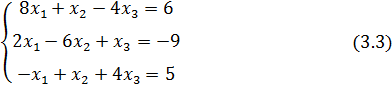
Прежде всего, убедимся, что итерационный метод Якоби можно использовать для заданной системы (3.3). Для этого проверим условие «преобладания диагональных коэффициентов» матрицы системы, что обеспечивает сходимость метода, т.е.
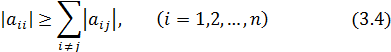
Приведем систему(3.3) к нормальному виду:
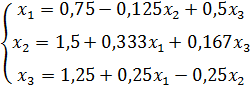(3.5)
Запишем систему в матричной форме
где
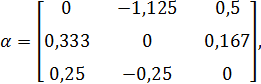
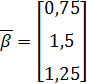
Формулы (3.5) будем использовать для построения итерационной последовательности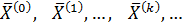 
где к – номер итерации.
Расчетная схема метода Якоби приведена на рис (3.4).
На практике итерационный процесс продолжается до тех пор, пока два соседних приближения не станут достаточно близкими.
Критерий близости двух приближений (двух векторов) может быть определен следующим образом:
· Рассмотрим вектор разности двух соседних итераций
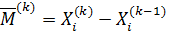
· Если норма этого вектора удовлетворяет условию
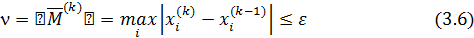
то итерационный процесс прекращается и за приближенное решение системы (3.3) с заданной точностью e принимается k -ое приближение, т.е.
Для проверки выполнения условия (3.6) используйте «условное форматирование » (рис.3.4)
Если условие (3.6) не выполнено, то итерационный процесс необходимо продолжить.
Анализируя результаты, принимаем за приближенное решение исходной системы с точностью e=0,1 четвертую итерацию, т.е. х1 =1,0196; х2 = 2,0217, х3 = 0,9909.
Изменяя значение e в ячейке G14 можно получить новое приближенное решение исходной системы с новой точностью.
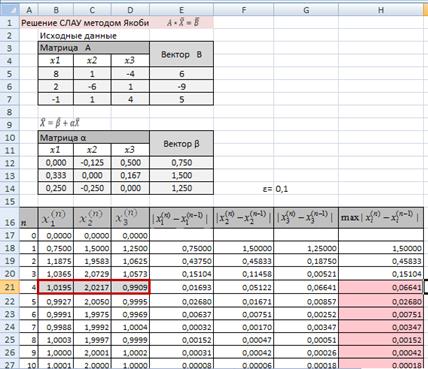
Рис.3.4. Расчетная схема метода Якоби
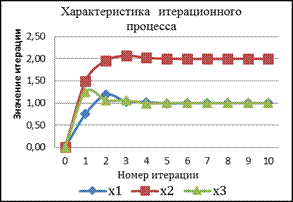
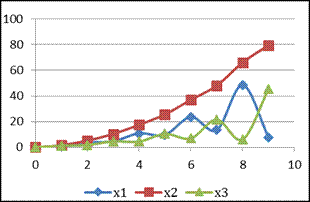
Проанализируйте сходимость итерационного процесса, построив графики (рис.3.5) изменения каждой компоненты вектора решения СЛАУ в зависимости от номера итерации.
| 
|
| Рис. 3.5. Иллюстрация сходящегося итерационного процесса | Рис. 3.6. Иллюстрация расходящегося итерационного процесса |
Задание 3.4. Проанализироватькорректность задачи (существование, единственность, устойчивость решения относительно исходных данных).
Порядок выполнения
1. Вычислите нормы матриц А и А-1 (можно вручную).
2. Исследуйте обусловленность матрицы, вычислив меру обусловленности m(А). Сделайте заключение об обусловленности матрицы A и заданной системы.
3. Проведите численный эксперимент: задайте небольшое возмущение исходных данных (элементов матрицы А, В (~0.1)) и снова решите систему, используя надстройку «Поиск решения». Проанализируйте, как изменились результаты.
4. Проанализировав полученные данные, сделайте заключение о корректности исходной задачи (существование, единственность, устойчивость решения).
Контрольные вопросы
1. Система линейных алгебраических уравнений (СЛАУ). Что является решением СЛАУ. Когда существует единственное решение СЛАУ.
2. Общая характеристика прямых (точных) методов решения СЛАУ. Метод Гаусса.
3. Общая характеристика итерационных методов решения СЛАУ. Метод Якоби (простых итераций).
4. Условия сходимости итерационных процессов.
5. Что понимают под термином корректности задачи решения СЛАУ.