ОКРУЖНОСТЬ. ОКРУЖНОСТИ, ВПИСАННЫЕ В ТРЕУГОЛЬНИК И ЧЕТЫРЕХУГОЛЬНИК
Окружность, касающаяся сторон угла
| C |
| B |
| A |
| O |
| D |
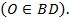
2. Отрезки, соединяющие точки касания с центром окружности, являются ее радиусами и перпендикулярны к сторонам угла
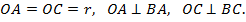
3. Расстояния от вершины угла до точек касания равны 
4. 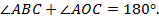
| B |
| A |
| C |
| O |
| P |
Взаимосвязь между отрезками касательной и секущей

Окружности, вписанные в треугольник и четырехугольник
| A |
| B |
| C |
| D |
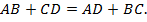
7. Параллелограмм, описанный около окружности, является ромбом.
8. Средняя линия трапеции, описанной около окружности, равна полусумме боковых сторон.
| A |
| B |
| C |
| D |
| O |
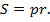
10. Центр окружности, вписанной в ромб, является точкой пересечения его диагоналей.
11. В трапеции 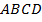 с основаниями
с основаниями  и
и  , описанной около окружности,
, описанной около окружности,

12. Диаметр окружности, вписанной в ромб (трапецию), является высотой ромба (трапеции).
13. Центр вписанной окружности является точкой пересечения биссектрис углов треугольника (четырехугольника).
14. Радиусы вписанной окружности, проведенные в точки касания, перпендикулярны к сторонам треугольника (четырехугольника).
15. Расстояния от вершины угла треугольника (четырехугольника) до точек касания вписанной окружности с его сторонами равны.
№1. Окружность с центром 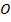 касается сторон угла
касается сторон угла  в точках
в точках 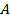 и
и  . Радиус окружности равен 7,
. Радиус окружности равен 7,  . Найдите
. Найдите 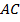 .
.
№2. Окружность с центром 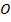 касается сторон угла
касается сторон угла  в точках
в точках 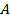 и
и  . Радиус окружности равен 6,
. Радиус окружности равен 6,  . Найдите площадь треугольника
. Найдите площадь треугольника  .
.
№3. Окружность с центром 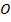 касается сторон угла
касается сторон угла  в точках
в точках 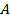 и
и  . Лучи
. Лучи  и
и 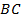 пересекаются в точке
пересекаются в точке 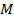 ,
, 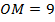 ,
, 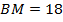 . Найдите площадь треугольника
. Найдите площадь треугольника  .
.
№4. Окружность, вписанная в равнобедренный треугольник 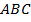 , касается его боковых сторон
, касается его боковых сторон 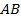 и
и 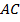 в точках
в точках 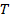 и
и 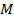 соответственно. Найдите
соответственно. Найдите  , если
, если  ,
,  .
.
№5. В треугольник 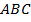 вписана окружность с центром
вписана окружность с центром 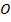 . Лучи
. Лучи  и
и  пересекают стороны
пересекают стороны 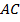 и
и 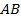 в точках
в точках 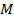 и
и 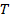 соответственно. Найдите
соответственно. Найдите 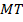 , если
, если 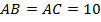 ,
,  .
.
| A |
| B |
| C |
| T |
| O |
| H |
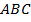 вписана окружность с центром
вписана окружность с центром 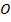 . Прямая, проходящая через точку
. Прямая, проходящая через точку 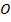 параллельно прямой
параллельно прямой 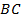 , пересекает стороны
, пересекает стороны 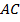 и
и 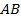 в точках
в точках 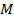 и
и 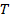 соответственно. Найдите
соответственно. Найдите 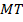 , если
, если 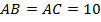 ,
, 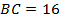 .
.
16. В равнобедренном треугольнике 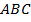 с основанием
с основанием 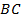 центр вписанной окружности лежит на биссектрисе
центр вписанной окружности лежит на биссектрисе  , являющейся также высотой и медианой треугольника.
, являющейся также высотой и медианой треугольника.  – радиус окружности, перпендикулярный боковой стороне. Из подобия треугольников
– радиус окружности, перпендикулярный боковой стороне. Из подобия треугольников  и
и  следуют формулы
следуют формулы

№6. Окружность с центром 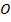 , вписанная в равнобедренный треугольник
, вписанная в равнобедренный треугольник 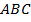 , касается его боковой стороны
, касается его боковой стороны 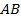 в точке
в точке 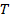 ,
,  ,
,  . Найдите основание
. Найдите основание 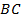 треугольника.
треугольника.
17. Длина гипотенузы  и полупериметр
и полупериметр  прямоугольного треугольника
прямоугольного треугольника 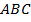 связаны с радиусом вписанной в него окружности
связаны с радиусом вписанной в него окружности  формулой
формулой
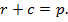
№7. Расстояние от вершины прямого угла треугольника до центра вписанной в треугольник окружности равно  , а площадь треугольника равна 30. Найдите длину гипотенузы.
, а площадь треугольника равна 30. Найдите длину гипотенузы.
№8. Окружность, вписанная в прямоугольный треугольник 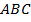 (
( ), касается катета
), касается катета 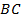 в точке
в точке  . Биссектриса угла
. Биссектриса угла 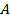 пересекает катет
пересекает катет 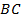 в точке
в точке 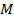 . Найдите
. Найдите  , если
, если  ,
,  .
.
№9. Окружность, вписанная в прямоугольный треугольник, делит гипотенузу на отрезки 6 и 8. Найдите площадь треугольника.
№10. Стороны треугольника равны 20, 20 и 24. В треугольник вписана окружность. Вторая окружность касается первой, одной из меньших сторон и большей стороны треугольника. Найдите радиус второй окружности.
№11. На основании 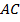 равнобедренного треугольника
равнобедренного треугольника 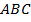 взята точка
взята точка  . В треугольники
. В треугольники  и
и 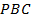 вписаны окружности. Найдите расстояние между точками касания этих окружностей с отрезком
вписаны окружности. Найдите расстояние между точками касания этих окружностей с отрезком  , если точка
, если точка  делит основание
делит основание 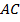 на отрезки
на отрезки  и
и  .
.
№12. Площадь круга, вписанного в трапецию, равна  , а сумма боковых сторон трапеции равна 20. Найдите площадь трапеции.
, а сумма боковых сторон трапеции равна 20. Найдите площадь трапеции.
№13. В прямоугольную трапецию вписана окружность. Расстояния от центра окружности до концов боковой стороны трапеции равны 6 и 8. Найдите площадь трапеции.
№14. Около окружности радиуса 3 описана равнобедренная трапеция, меньшее основание которой равно 8. Найдите площадь трапеции.
№15. В ромб вписана окружность. Точка касания окружности и стороны ромба делит сторону в отношении  . Площадь ромба равна
. Площадь ромба равна  . Найдите радиус окружности.
. Найдите радиус окружности.