Исследование функции, заданной графически»

09.11.2021

Уроки 9-10. Тема: «График функции. Чтение графиков функций.

Исследование функции, заданной графически»

Задание №1. Ознакомьтесь с теорией по данной теме. (УСТНО!)

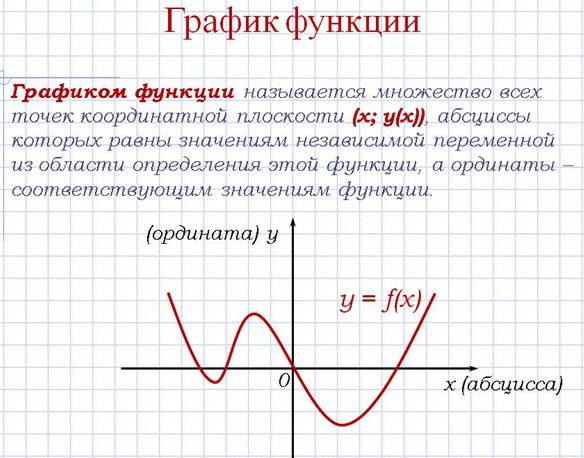
По графику функции можно легко найти все свойства функции: область определения, четность и периодичность, нули функции, промежутки возрастания и убывания, промежутки постоянного знака, точки экстремума, наибольшее и наименьшее значения функции, множество значений функции. Подробнее на примерах рассмотрите.

Свойства функции на графике	Примеры
1. Область определения. Обозначается D(f). Смотрите по оси Ox, промежуток записываем слева-направо. Если крайние точки выколотые, то скобки ставим круглые; если точки закрашенные, то скобки квадратные.	D(f):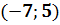
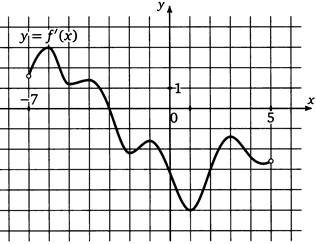
2. Нули функции – это точки пересечения с осью Ox. Если значение неточное, пишите приближенно. Если на графике нет чисел, сами расставляете.	На данном рисунке таких точек три: х=-3; х=2; х=6-нули функции
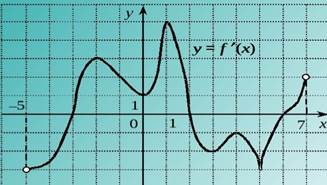
3. Четность. Возможны три случая: функция четная, если график симметричен относительно оси Оy (одинаковый слева и справа от оси Оy) функция нечетная, если график симметричен относительно точки (0;0) (одинаковый крест-накрест) функция ни четная, ни нечетная, если график не симметричен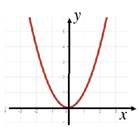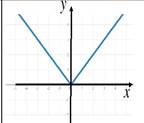
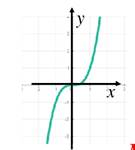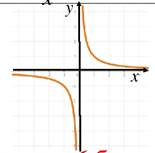
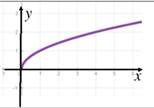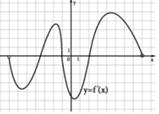
4. Периодичность График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов. Периодом функции называется длина промежутка между соответствующими точками одинаковых фрагментов
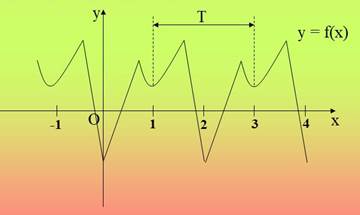
5. Промежутки монотонности (возрастания и убывания). Выписать промежутки по оси Ox, когда график идет вверх, растет (функция возрастает), и когда падает вниз (убывает). Промежутки монотонности записывают в квадратных скобках.	Например, на этом рисунке синим цветом выделены промежутки убывания (-9;-7], [-5;-4],[1;3], [7;8) 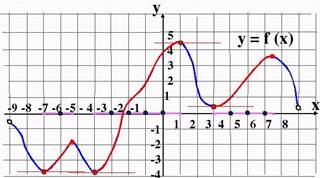красным цветом выделены промежутки возрастания функции [-7;-5], [-4;1],[3;7]
6. Промежутки знакопостоянства y>0 и y<0 записываются по оси Ох. y>0 промежутки, на которых график расположен выше оси Ох y<0 промежутки, на которых график расположен ниже оси Ох Эти промежутки записываются в круглых скобках всегда	На данном рисунке промежутки, когда y>0 выделены зеленым цветом? А когда y<0 – сиреневым цветом y>0 при 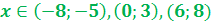y<0 при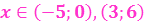
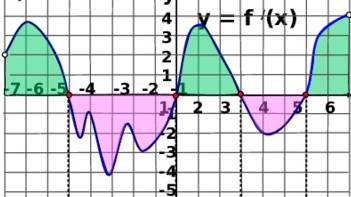
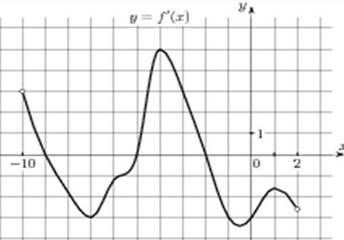
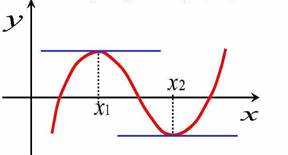
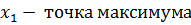
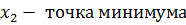
7. Точки экстремума: точки максимума и точки минимума. Выписываются по оси Ох! На графике точки максимума – это все «вершины графика» (все верхние точки), а точки минимума- все нижние точки. В точках максимума образуется «горка», а в точках минимума -«ямка». Крайние точки не учитываем!	На данном рисунке точек максимума 2, точек минимума 2.
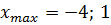
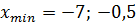
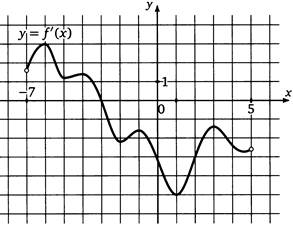
8. Наибольшее и наименьшее значения функции. Обозначается самая высокая и самая низкая точка на графике. Смотрим по оси Оy!
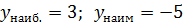
9. Множество значений функции- записываем по оси Оy промежуток от самой низкой точки, до самой высокой. Это свойство 7, записанное в виде промежутка.	E(y): [-5;3] (для предыдущего рисунка)

Задание №2. Разберите по примеру исследование функции, заданной графически. Перечертите схематично график и запишите свойства себе в тетрадь (пример №1).

Пример №1. Проведите по общей схеме исследование функции, заданной графиком.

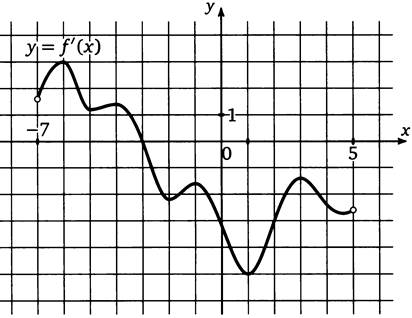
1. D(f):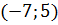

2. Нули функции: x = -3.

3. Функция ни четная, ни нечетная (так как график не симметричен)

4. Функция непериодическая

5. Функция убывает на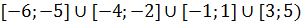

Функция возрастает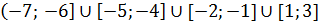

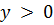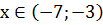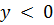6. при ; при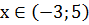

7.

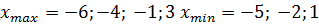
8.

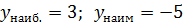
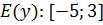
Задание №3. Выполните самостоятельно по образцу 1 пример (любой на ваш выбор, напишите только номер, рисунок перечерчивать не нужно), присылаете мне решение (9 пунктов, записанные, как в примере 1).

Проведите исследование функции по ее графику.
1.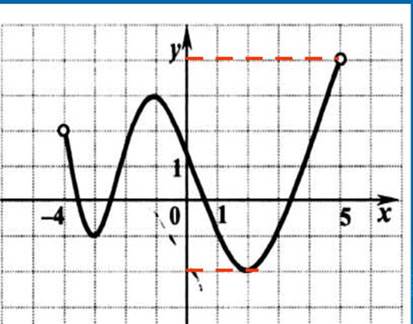
2.
3.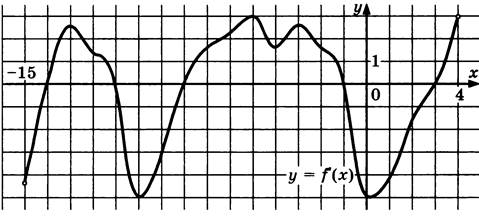
4.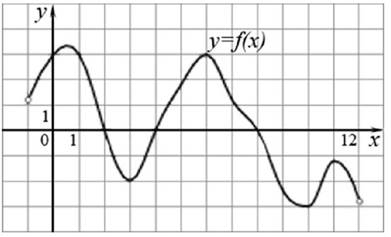
5.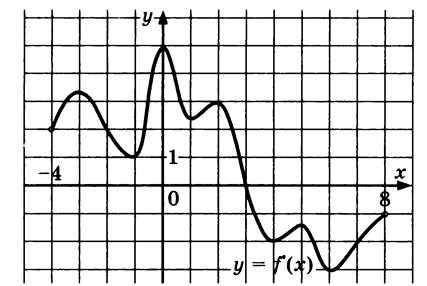
6.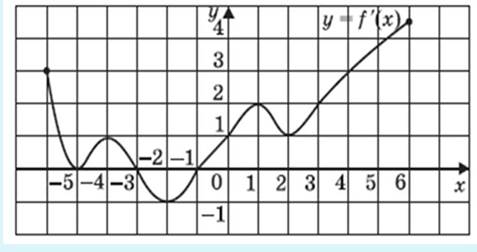
7.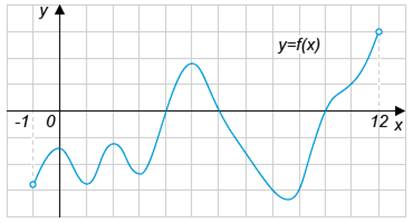
8.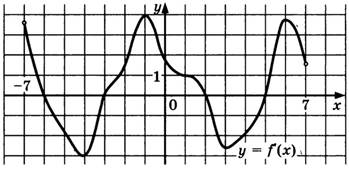
9.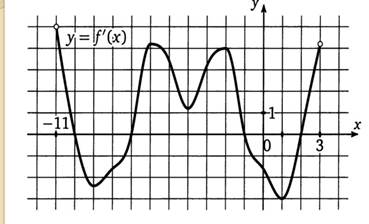
10.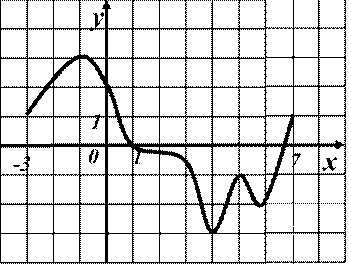
11.
12.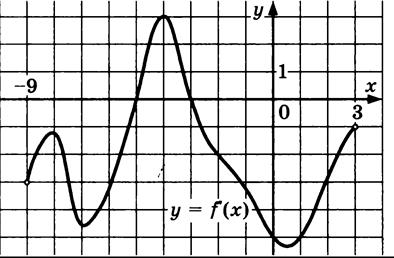
13.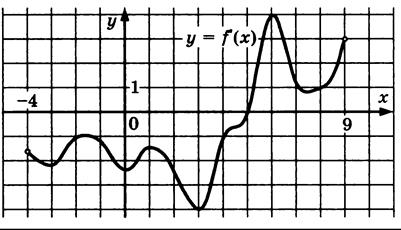
14.
15.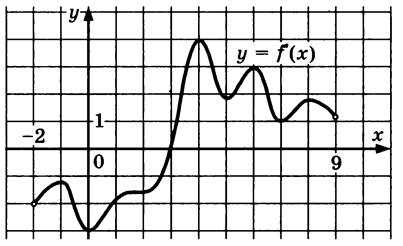