Свойства правильной пирамиды.

Тема: «Пирамида. Объём и площадь поверхности пирамиды »

План

1. Понятие пирамиды.

2. Правильная пирамида и её свойства.

3. Усечённая пирамида. Площадь боковой поверхности усечённой пирамиды.

4. Объём пирамиды.

5. Решение задач.

Цели и задачи занятия:

Обучающие: изучить новый вид многогранников – пирамиды. Выйти на понятия правильной и усечённой пирамиды. Рассмотреть задачи, связанные с нахождением объёма и площади поверхности пирамиды.

Развивающие: развивать познавательный интерес через творческую активность, исследовательскую деятельность на основе умения делать обобщения по данным, полученным в результате исследования.

Воспитательные: прививать навыки математического мышления, побуждать к научной, творческой деятельности студентов, формировать умение мыслить пространственно, анализировать, наблюдать, делать выводы, воспитывать внимание, дисциплинированность, активность.

Понятие пирамиды.

Рассмотрим многоугольник A₁A₂...A_n и точку Р, не лежащую в плоскости этого многоугольника (рис.1). Соединив точку Р с вершинами многоугольника, получим n треугольников: PA₁A₂, PA₂A₃,…, PA_nA₁. (1)

Определение. Многогранник, составленный из n-угольника A₁A₂...A_n и n треугольников (1), называется пирамидой.

Многоугольник A₁A₂...A_n называется основанием, а треугольники PA₁A₂, PA₂A₃,…, PA_nA₁ – боковые грани пирамиды, отрезки PA₁, PA₂,…, PA_n – боковые ребра пирамиды, точка Р – вершина пирамиды.

Пирамиду с основанием A₁A₂...A_n и вершиной Р называют n-угольной пирамидой и обозначают PA₁A₂...A_n.

Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды. На рисунке 1 PH является высотой. Обратите внимание, что высота может лежать и вне пирамиды (рис. 2) или быть одним из боковых ребер (рис. 3).

		Рис.2 Высота вне пирамиды
		Рис.1 Пирамида			Рис.3 Высота пирамиды - боковое ребро

Площадь полной поверхности пирамиды

Площадью полной поверхности пирамиды называются сумма площадей всех ее граней, а площадью боковой поверхности пирамиды – сумма площадей ее боковых граней.

Для пирамиды, верно равенство S_полн= S_бок+S_осн.

2. Правильная пирамида и её свойства.

Определение. Будем называть пирамиду правильной, если ее

основание – правильный многоугольник, а отрезок, соединяющий

вершину пирамиды с центром основания, является ее высотой.

Напомним, что центром правильного многоугольника называется

центр вписанной в него (или описанной около него) окружности

Свойства правильной пирамиды.

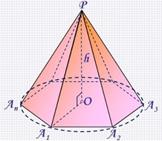
Рассмотрим правильную пирамиду PA₁A₂...A_n (рис. 4). Пусть О – центр описанной около основания окружности, тогда РО – высота пирамиды, значит РО перпендикулярен любой прямой, лежащей в плоскости основания. Таким образом, высота РО перпендикулярна радиусам А₁О, А₂О,...А_nО.

Образованные высотой и радиусами треугольники являются прямоугольными. Причем, эти треугольники имеют общий катет – РО и равные катеты А₁О, А₂О,...А_nО (равны как радиусы). Значит, треугольники РОА₁, РОА₂,...РОА_n равны по двум катетам, значит равны гипотенузы PA_1, РA₂... РA_n, которые являются боковыми ребрами правильной пирамиды.

Боковые ребра пирамиды равны, значит боковые грани – равнобедренные треугольники. Основания этих треугольников равны друг другу, так как в основании лежит правильный многоугольник. Следовательно, боковые грани равны по третьему признаку равенства треугольников.

Таким образом, верны следующие утверждения:

· Все боковые ребра правильной пирамиды равны.

· Боковые грани правильной пирамиды являются равными равнобедренными треугольниками.

Определение. Апофемой называется высота боковой грани правильной пирамиды, проведенная из ее вершины. На рис.4 PE – одна из апофем. Все апофемы правильной пирамиды равны друг другу как высоты в равных треугольниках.

Теорема. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Доказательство

Боковые грани правильной пирамиды - равные равнобедренные треугольники, основания которых - стороны основания пирамиды, а высоты равны апофеме. Площадь S боковой поверхности пирамиды равна сумме произведений сторон основания на половину апофемы d. Вынося множитель за скобки, получим в скобках сумму сторон основания пирамиды, т. е. его периметр. Теорема доказана.