Пирамида. Усеченная пирамида
Определение 1
Многогранник, у которого одна грань есть многоугольник, а все остальные грани — треугольники с общей вершиной, называется пирамидой.
Многоугольная грань пирамиды называется ее основанием, треугольные грани с общей вершиной — боковыми гранями, а их общая вершина — вершиной пирамиды.
Пирамиды в зависимости от числа сторон основания подразделяются на треугольные (они называются тетраэдрами), четырехугольные, пятиугольные и т.д.
Определение 2
Пирамида называется правильной, если:
1) основание есть правильный многоугольник,
2) высота проходит через центр этого многоугольника.
Пирамиду можно получить, если пересечь многогранный угол плоскостью, имеющей общие точки со всеми ребрами.
В правильной пирамиде радиусы правильного многоугольника, лежащего в основании, являются проекциями боковых ребер, поэтому эти ребра равны, а следовательно, равны все боковые грани, являющиеся равнобедренными треугольниками.
Определение 3
Апофемой правильной пирамиды называется высота ее боковой грани.
Определение 4
Усеченной пирамидой называется часть пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию.
Параллельные грани называются основаниями, а отрезок перпендикуляра, заключенный между основаниями, называется высотой усеченной пирамиды.
Определение 5
Усеченная пирамида называется правильной, если она составляет часть правильной пирамиды.
Правильную пирамиду или правильную призму не следует путать с правильным многогранником. Многогранник называется правильным, если все его грани — равные правильные многоугольники и все многогранные углы равны (например, куб или правильный тетраэдр).
|
|
Боковые грани правильной усеченной пирамиды являются равными равнобочными трапециями и многоугольники оснований подобны.
Определение 6
Высота боковой грани (трапеции) называется апофемой усеченной пирамиды.
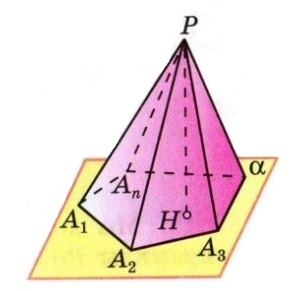
Высота пирамиды
Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды. На рисунке 1 PH является высотой. Обратите внимание, что высота может лежать и вне пирамиды (рис. 3) или быть одним из боковых ребер (рис. 4).
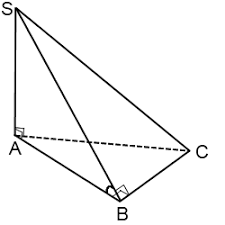АS - высота пирамиды
НS - высота пирамиды, которая расположена вне пирамиды.
Правильная пирамида
Будем называть пирамиду правильной, если ее основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой. Напомним, что центром правильного многоугольника называется центр вписанной в него (или описанной около него) окружности (рис.5).
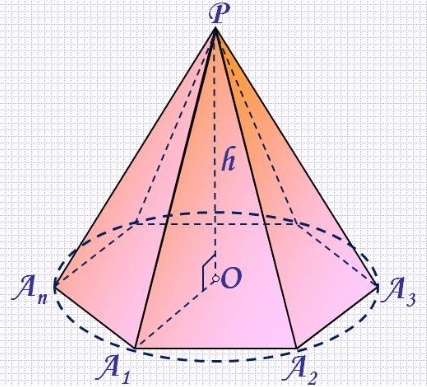
Рисунок 5 – Правильная пирамида
Правильная пирамида обладает несколькими хорошими свойствами. Давайте выясним, какими.
Рассмотрим правильную пирамиду PA1A2...An (рис. 5).
Пусть О – центр описанной около основания окружности, тогда РО – высота пирамиды, значит РО перпендикулярен любой прямой, лежащей в плоскости основания. Таким образом, высота РО перпендикулярна радиусам А1О, А2О,...АnО.
Образованные высотой и радиусами треугольники являются прямоугольными. Причем, эти треугольники имеют общий катет – РО и равные катеты А1О, А2О,...АnО (равны как радиусы). Значит, треугольники РОА1, РОА2,...РОАn равны по двум катетам, значит равны гипотенузы PA1, РA2... РAn, которые являются боковыми ребрами правильной пирамиды.
|
|
Боковые ребра пирамиды равны, значит боковые грани – равнобедренные треугольники. Основания этих треугольников равны друг другу, так как в основании лежит правильный многоугольник. Следовательно, боковые грани равны по третьему признаку равенства треугольников.
Таким образом, верны следующие утверждения:
· Все боковые ребра правильной пирамиды равны.
· Боковые ребра правильной пирамиды являются равными равнобедренными треугольниками.
Введем еще одно определение. Апофемой называется высота боковой грани правильной пирамиды, проведенная из ее вершины. На рисунке 5 PE – одна из апофем.
Все апофемы правильной пирамиды равны друг другу как высоты в равных треугольниках.
Усеченная пирамида
Возьмем произвольную пирамиду PA1A2...An и проведем секущую плоскость β, параллельную плоскости основания пирамиды α и пересекающую боковые ребра в точках В1,В2,...Вn (рис. 6). Плоскость β разбивает пирамиду на два многогранника. Многогранник, гранями которого являются n-угольники A1A2...An и В1В2...Вn (нижнее и верхнее основания соответственн о), расположенные в параллельных плоскостях и n четырехугольников A1A2B2B1, A2A3B3B2, … A1AnBnB1 (боковые грани), называется усеченной пирамидой.
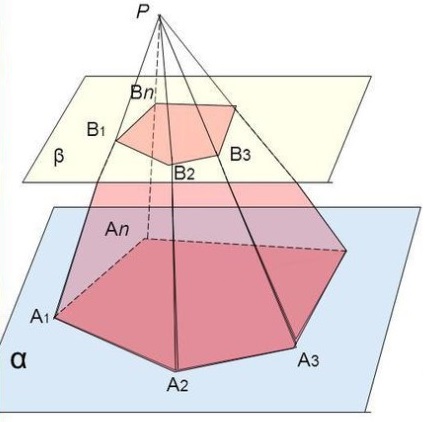
Рисунок 6 – Усеченная пирамида
Отрезки A1B1, A2B2, … AnBn называют боковыми ребрами усеченной пирамиды.
Усеченную пирамиду с основаниями A1A2...An и В1В2...Вn обозначают следующим образом: A1A2...AnВ1В2...Вn.
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания называется высотой усеченной пирамиды. На рисунке 7 отрезки HH1 и В1O –высоты усеченной пирамиды.
|
|
Рисунок 7 – Высота усеченной пирамиды
Площадь поверхности пирамиды
Площадью полной поверхности пирамиды называются сумма площадей всех ее граней, а площадью боковой поверхности пирамиды – сумма площадей ее боковых граней.
Для пирамиды, верно равенство Sполн= Sбок+Sосн.
Докажем теорему для площади боковой поверхности правильной пирамиды.
Теорема. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Для площади боковой поверхности усеченной пирамиды верна следующая теорема
Теорема. Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.