II. Локальная и интегральная теоремы Лапласа

ПОВТОРЕНИЕ ИСПЫТАНИЙ

 

ПЛАН ЛЕКЦИИ

I. Схема испытаний Бернулли. Формулы Бернулли и Пуассона

II. Локальная и интегральная теоремы Лапласа

 

I. Схема испытаний Бернулли. Формулы Бернулли и Пуассона. При практическом применении теории вероятностей часто встречаются задачи, в которых одно и то же испытание повторяется несколько раз. В результате каждого опыта может появиться или не появиться некоторое событие . При этом испытателя интересует не результат каждого отдельного испытания, а общее число появлений события в результате серии испытаний.

Испытания называются независимыми относительно события , если в каждом испытании вероятность события не зависит от исходов других испытаний.

Будем рассматривать такие независимые испытания, в которых событие имеет одну и ту же вероятность .

Введем понятие сложного события, понимая под ним совмещение нескольких отдельных событий, которые называются простыми.

Пусть производится независимых испытаний, в каждом из которых событие может появиться или не появиться, , .

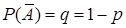Найдем вероятность того, что при испытаниях событие появится раз и не появится раз, причем не требуется, чтобы событие наступило в определенной последовательности. Например, при трех появлениях события в четырех испытаниях возможны следующие сложные события: , , , .

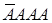Вероятность одного сложного события, состоящего в том, что в испытаниях событие наступит раз и не наступит раз, по теореме умножения вероятностей независимых событий, равна . Таких сложных событий может быть столько, сколько можно составить сочетаний из элементов по , то есть . Эти сложные события несовместны, тогда, по теореме сложения вероятностей несовместных событий, искомая вероятность равна сумме вероятностей всех возможных сложных событий. Вероятности этих сложных событий одинаковы, поэтому вероятность появления события раз в испытаниях равна вероятности одного сложного события, умноженной на их число:

 

. (1)

 

Эта формула называется формулой Бернулли.

Пример 1. Два равносильных противника играют в шахматы. Что вероятнее: выиграть одну партию из двух или две партии из четырех? Ничьи во внимание не принимаются.

Решение. Так как противники равносильные, вероятности выигрыша и проигрыша в одной партии для каждого из них равны, 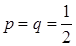. Найдем вероятность выиграть одну партию из двух по формуле Бернулли (1):

 

.

 

Аналогично найдем вероятность выиграть две партии из четырех:

 

.

 

Так как , то вероятнее выиграть одну партию из двух.

С помощью формулы Бернулли можно вычислить следующие вероятности:

1) вероятность того, что в независимых испытаниях событие наступит менее раз,

 

; (2)

 

2) вероятность того, что в независимых испытаниях событие наступит более раз,

 

; (3)

 

3) вероятность того, что в независимых испытаниях событие наступит не менее раз,

 

; (4)

4) вероятность того, что в независимых испытаниях событие наступит не более раз,

 

. (5)

 

Пример 2. Игральный кубик бросают пять раз. Найти вероятность того, что одно очко выпадет: 1) менее трех раз; 2) не менее трех раз.

Решение. Вероятность того, что при одном броске кубика выпадет одно очко, равна . Вероятность того, что одно очко не выпадет, . Вероятность того, что при пяти бросках кубика одно очко выпадет менее трех раз, найдем по формуле (2):

 

.

 

Вероятность того, что при пяти бросках кубика одно очко выпадет не менее трех раз, найдем по формуле (4):

 

.

Заметим, что события «одно очко выпало менее пяти раз» и «одно очко выпало НЕ менее пяти раз» противоположные. Поэтому сумма их вероятностей равна 1.

Если число испытаний велико, а вероятность появления события в каждом испытании очень мала, то используется приближенная формула

 

, (6)

 

где – среднее число появлений события в независимых испытаниях. Эта формула называется формулой Пуассона.

Пример 3. Экспериментатор 1000 раз снимает показания измерительных приборов. Вероятность того, что погрешность при снятии показания превысит допустимую, равна 0,01. Найти вероятность того, что 5 показаний будут сняты с превышением допустимой погрешности.

Решение. Событие – погрешность при снятии одного показания прибора превысит допустимую, (вероятность события мала). Число снятых показаний велико. Поэтому для нахождения вероятности того, что 5 показаний будут сняты с превышением допустимой погрешности, можно использовать формулу Пуассона ():

 

.

 

Ответ: .

II. Локальная и интегральная теоремы Лапласа. При большом числе испытаний использовать формулу Бернулли (1) трудно, так как она требует выполнения действий над большими числами.

Если число испытаний велико, то можно использовать локальную теорему Лапласа, которая дает асимптотическую формулу, позволяющую приближенно найти вероятность появления события ровно раз в испытаниях.

Теорема 1 (локальная теорема Лапласа): если вероятность появления события в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие появится в испытаниях ровно раз, приближенно равна (тем точнее, чем больше ) значению функции

 

, (7)

где .

Значения функции , соответствующие положительным значениям , приведены в таблицах. Функция четная, то есть . Функция называется функцией Гаусса.

Итак, , где .

Пример 4. На опытном участке посеяно 10000 зерен пшеницы. Вероятность того, что одно зерно взойдет, равна 0,9. Найти вероятность того, что взойдет 9000 зерен.

Решение. По условию, , , , . Используем локальную теорему Лапласа:

 

.

Ответ: .

Для вычисления вероятности того, что событие появится в независимых испытаниях не менее и не более раз, используется интегральная теорема Лапласа.

Теорема 2 (интегральная теорема Лапласа): если вероятность появления события в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие появится в независимых испытаниях не менее и не более раз, приближенно равна определенному интегралу

 

, (8)

 

где , .

Значения интеграла для приведены в таблицах. Функция нечетная, то есть . Функция называется функцией Лапласа.

Для того, чтобы использовать таблицу значений функции Лапласа, преобразуем формулу (8):

 

, (9)

 

где , .

Пусть – число появлений события в независимых испытаниях, в каждом из которых вероятность наступления события постоянна и равна . Если число изменяется от до , то дробь изменяется от до . Тогда интегральную теорему Лапласа можно записать в виде

. (10)

 

Пример 5. На опытном участке посеяно 10000 зерен пшеницы. Вероятность того, что зерно взойдет, равна 0,9. Найти вероятность того, что взойдет от 8990 до 9020 зерен.

Решение. По условию, , , , , . Используем интегральную теорему Лапласа:

.

Ответ: .

Найдем вероятность того, что отклонение относительной частоты появления события от его постоянной вероятности по абсолютной величине не превышает заданного положительного числа , то есть найдем вероятность выполнения неравенства

 

. (11)

 

Заменим неравенство (11) равносильным ему:

 

или

.

 

Умножим все части этого неравенства на множитель :

 

. (12)

 

Неравенства (11) и (12) являются равносильными, поэтому найдем вероятность выполнения неравенства (12). Используем для этого интегральную теорему Лапласа в форме (10): , , тогда

 

.

 

Заменяя неравенства в скобках равносильным исходным неравенством, получим

. (13)

 

Пример 6. Вероятность появления события в каждом из 625 независимых испытаний равна 0,8. Найти вероятность того, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более чем на 0,02.

Решение. По условию, , , , . Используя формулу (13), найдем вероятность

 

.

Ответ: 0,7888.

Число наступлений события в независимых испытаниях, в каждом из которых вероятность появления события постоянна и равна , называется наивероятнейшим, если вероятность того, что событие наступит в этих испытаниях раз, превышает (или, по крайней мере, не меньше) вероятностей остальных возможных исходов испытаний.

Наивероятнейшее число определяется из двойного неравенства

 

. (14)

 

Если число дробное, то существует одно наивероятнейшее число . Если число целое, то существуют два наивероятнейших числа и . Если число целое, то наивероятнейшее число .

Пример 7. Производится 35 бросков игрального кубика. Найти наивероятнейшее число появлений одного очка.

Решение. Вероятность выпадения одного очка , тогда . Наивероятнейшее число найдем по формуле (14), , , тогда , то есть существуют два наивероятнейших числа появлений одного очка: 5 и 6. Аналогичные наивероятнейшие числа получаются для любого другого количества очков.

Ответ: 5; 6.