ЛЕКЦИЯ 2
ПРЯМАЯ ЛИНИЯ
Для построения изображения прямой линии на плоскостях проекций достаточно построить проекции двух точек этой прямой (рис.1).
|
| Рис.1 |
a([ВВ2] || [АА2]) ∩ 
= a2
([АА1] || [ВВ1]) ∩ 
= a1
а –прямая в пространстве, a 1 – горизонтальная проекция прямой, а 2 – фронтальная проекция прямой.
Проекция прямой линии есть также прямая линия.
Точка, лежащая на прямой линии, имеет свои проекции на соответствующих проекциях прямой. C1 
[А1В1]; C2 [А2В2].
В каком отношении точка делит отрезок прямой линии в пространстве, в таком же отношении проекции этой точки делят соответствующие проекции отрезка.
.
Совмещая плоскости проекций и строим эпюр отрезка [АВ]. Так как в дальнейшем будут рассматриваться только безосные эпюры, определим разницу между эпюром с осями и безосным эпюром.
По эпюру с осями можно определить положение точек А и В в пространстве по координатам X, Y, Z. Безосный эпюр точек А и В не определяет их положение в пространстве, но позволяет судить об их относительности ориентировке (рис.2).
∆Х характеризует смещение точки А по отношению к точке В в направлении параллельном и . Относительное смещение точки в направлении перпендикулярном плоскости определяется отрезком ∆У; отрезок ∆Z показывает превышение точки В над точкой А.
|
| ||
| Эпюр с осями | Безосный эпюр | ||
| Рис.2. | |||
Положение прямой относительно плоскостей проекций.
1. Прямыми общего положения называются прямые, не параллельные ни одной из плоскостей проекций (рис.1, 2, 3).
|
| Рис. 3 |
2. Прямые уровня - прямые, параллельные плоскостям проекций.
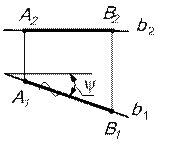
а) Прямые, параллельные горизонтальной плоскости проекций, называются горизонтальными прямыми или горизонталями (рис.4)
| 
|
| Рис.4. |
[АВ] b
[А1В1] b1
[А2В2] b2
b2 ┴ линии связи;
b2 ║ ОХ
b1 – конгруэнтна самой прямой
б) Прямая, параллельная , называется фронтальной прямой или фронталью (рис.5).
| 
|
| Рис. 5 |
[CD] c
[C1D1] c1
[C2D2] c2
c1┴ линии связи
c1║ ОХ
c2 конгруэнтна самой прямой
в) Прямая, параллельная 
называется профильной прямой (рис.6). d2 
OX, d1 OX, d3- конгруэнтна самой прямой.
| 
|
| Рис.6. |
[MN] d
[M1N1] d1
[M2N2] d2
3. Прямые, перпендикулярные плоскостям проекций, называются проецирующими.
Прямая, перпендикулярная , называется горизонтально-проецирующей прямой. Одна из проекций превращается в точку, а другая совпадает с линией проекционной связи и конгруэнтна самой прямой (рис.7). n , [АВ] n; [А2В2] n2; А1 
В1 n1.
| 
|
| Рис. 7 |
Прямая, перпендикулярная , называется фронтально-проецирующей прямой (рис.8). m , [CD] m; [C1D1] m1; C2 D2 m2; m1 конгруэнтна m.
| 
|
| Рис. 8 |
Прямая, перпендикулярная , называется профильно-проецирующей прямой (рис.9). ℓ , [MN] ℓ; [M1N1] ℓ 1; [M2N2] ℓ 2 ; [M1N1]=[M2N2]=[MN].
|
|
| Рис. 9 |
Прямая, параллельная плоскости симметрии 
(рис.10).
Прямая, параллельная плоскости тождества 
(рис.11).
| 
|
| Рис. 10 | Рис.11 |
ОПРЕДЕЛЕНИЕ ДЛИНЫОТРЕЗКА ПРЯМОЙ ЛИНИИ И УГЛОВ НАКЛОНА ЕЕ К ПЛОСКОСТЯМ ПРОЕКЦИЙ
Величина отрезка прямой линии в пространстве выражается гипотенузой прямоугольного треугольника, один катет которого равен проекции отрезка на плоскость, а другой разности удалений концов отрезка от той же плоскости проекций (рис.12).
|
АВ0 ║ А1В1
Δ АВВ0 – прямоугольный
АВ - истинная величина отрезка
АВ0 = А1В1
ВВ0 = ZВ – ZА= ΔZ
ВВ1 = ZВ; В0В1 = АА1 = ZА
<φ – угол наклона прямой к плоскости проекций
<Ψ - угол наклона прямой к плоскости проекций
|
| Рис.2.12 |
Истинная величина отрезка [АВ] определяется гипотенузой прямоугольного треугольника, у которого один катет [АВ0]=[А1В1], а второй ∆Z = ZВ - ZА. Угол φ определяется между отрезком [АВ] и горизонтальной проекцией [А1В1]= [АВ0].
Истинная величина отрезка определяется как гипотенуза прямоугольного треугольника, у которого один катет [АВ0]=[А1В1], а второй ∆Y = YВ - YА. Угол Ψ определяется между отрезком [АВ] и фронтальной проекцией [А2В2]= [АВ0].
Рассмотрим пример определения истинной величины отрезка [АВ] на эпюре (рис.13).
|
| Рис. 13 |