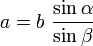Реферат
на тему: Решение треугольников
Выполнила: Зарипова Э.
Проверила: Газизова А.Х
2013 год.
Решение треугольников — исторический термин, означающий решение главной тригонометрической задачи: по известным данным о треугольнике (стороны, углы и т. д.) найти остальные его характеристики. Треугольник может располагаться на плоскости или на сфере. Данная задача часто встречается в тригонометрических приложениях, например, в геодезии, астрономии, строительстве, навигации.
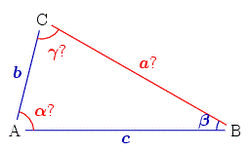
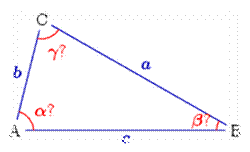
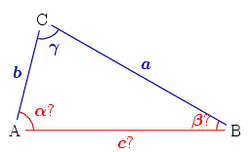
У треугольника общего вида имеется 6 основных характеристик: 3 линейные (длины сторон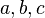 
) и 3 угловые (
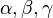), см. рисунок. В классической задаче плоской тригонометрии заданы 3 из этих 6 характеристик, и нужно определить 3 остальные. Очевидно, если известны только 2 или 3 угла, однозначного решения не получится, так как любой треугольник, подобный данному, тоже будет решением, поэтому будем считать, что хотя бы одна из известных величин — линейная.
Стандартным методом решения задачи является использование нескольких фундаментальных соотношений, выполняющихся для всех плоских треугольников:
Теорема косинусов
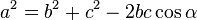
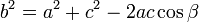
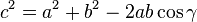
Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
Теорема синусов
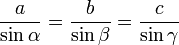
Теорема синусов. Стороны треугольника пропорционально синусам противоположных углов
Сумма углов треугольника
Три стороны
Пусть заданы длины всех трёх сторон 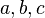. Чтобы найти углы 
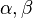, воспользуемся теоремой косинусов:
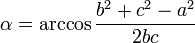
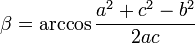
Третий угол сразу находится из правила, что сумма всех трёх углов должна быть равна 180°.
В некоторых источниках предлагается второй угол найти по теореме синусов, но, как указано в вышеприведенном замечании 1, при этом существует опасность спутать тупой угол с острым.
Ещё один метод вычисления углов по известным сторонам: использование теоремы котангенсов.
Две стороны и угол между ними
Пусть, для определённости, известны длины сторон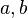 
и угол 
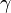между ними. Для определения длины стороны 
вновь воспользуемсятеоремой косинусов:
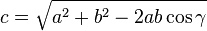
Мы фактически свели задачу к предыдущему случаю. Далее воспользуемся теоремой косинусов для нахождения второго угла:
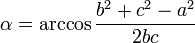
Третий угол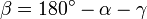 
.
Две стороны и угол не между ними
Этот случай самый сложный и неоднозначный. Пусть, например, известны две стороны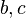 
и угол 
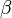. Уравнение для угла 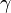найдём изтеоремы синусов
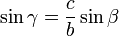
Для краткости обозначим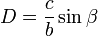 
(правая часть уравнения). При решении уравнения возможны 4 случая.
Если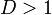 
, такого треугольника не существует (сторона 
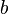«не достаёт» до линии BC).
Если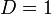 
, существует единственное решение, причём треугольник прямоугольный, 
.
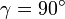Если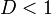 
, то возможны 2 варианта.
Если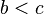 
, то угол 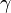имеет два возможных значения: острый угол 
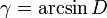и тупой угол 
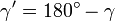. На рисунке справа первому значению соответствуют точка 
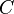, сторона 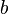и угол 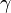, а второму значению — точка 
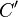, сторона 
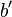и угол 
.
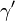Если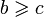 
, то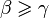 
(как известно, большей стороне треугольника соответствует больший противолежащий угол). Поскольку в треугольнике не может быть двух тупых углов, тупой угол для 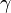исключён, и решение 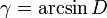единственно.
Третий угол находится как обычно: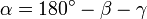 
. Третью сторону можно найти по теореме синусов:
