Основу математических моделей многих процессов и явлений в физике, химии, биологии, экономике и других областях составляют уравнения различного вида: нелинейные уравнения, обыкновенные дифференциальные уравнения, дифференциальные уравнения в частных производных и т.д. Для решения подобных уравнений необходимо иметь возможность вычислять значения функций, входящих в описание математической модели рассматриваемого процесса или явления, при произвольном значении аргумента. Для сложных моделей подобные вычисления могут быть трудоемкими даже при использовании компьютера.
Используемые в математических моделях функции могут быть заданы как аналитическим способом (в виде формулы), так и табличным, при котором функция известна только при определенных дискретных значениях аргумента. Например, если функциональная зависимость получена в результате расчетов, проведенных на ЭВМ, или в процессе измерений, осуществленных в рамках какого-либо эксперимента, то она оказывается заданной именно табличным способом. На практике же нам могут понадобиться значения функции и в других точках, отличных от тех, что заданы в таблице. Однако напрямую получить эти значения можно только путем сложных расчетов или проведением дорогостоящих экспериментов.
Таким образом, с точки зрения экономии времени и средств мы приходим к задаче вычисления приближенных значений функции при любом значении аргумента на основе имеющихся табличных данных.
Эта задача решается путем приближенной замены функции f(x) более простой функцией j(x), которую нетрудно вычислять при любом значении аргумента x в заданном интервале его изменения. Введенную функцию можно использовать не только для приближенного определения численных значений f(x), но и для проведения аналитических расчетов при теоретическом исследовании модели.
|
|
Итак, пусть изучая неизвестную функциональную зависимость между y и x, мы имеем таблицу значений
| x 0 | x 1 | ... | xn |
| y 0 | y 1 | ... | yn |
Задача состоит в том, чтобы найти приближенную зависимость φ(х) для таблично заданной функции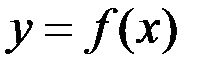 
значения которой при 
мало отличаются от опытных данных yi.
Такое приближение функции f(x) более простой функцией j(x) называется аппроксимацией (от латинского approximo – приближаюсь). Аппроксимирующую функцию j(x) строят таким образом, чтобы отклонения (в некотором смысле) j(x) от f(x) в заданной области было наименьшим. Понятие “малого отклонения” зависит от того, каким способом оценивается близость двух функций, поэтому оно будет уточняться в дальнейшем при рассмотрении конкретных методов аппроксимации. Аппроксимация бывает двух видов: точечная и непрерывная.
Непрерывная аппроксимация. Если исходная функция f(x) задана аналитическим выражением, то при построении аппроксимирующей функции j(x) возможно требовать минимальности отклонения одной функции от другой на некотором непрерывном множестве точек, например, на отрезке [ a,b ]. Такой вид аппроксимации называется непрерывным или интегральным.
Теоретически для наилучшего приближения целесообразно требовать, чтобы во всех точках некоторого отрезка [ a,b ] отклонения аппроксимирующей функции j(x) от функции f(x) было по абсолютной величине меньше заданной величины e>0:
.
В этом случае говорят, что функция j(x) равномерно приближает функцию f(x) с точностью e на интервале [ a,b ]. Практическое получение равномерного приближение представляет большие трудности, и поэтому этот способ применяется главным образом в теоретических исследованиях.
|
|
Наиболее употребительным является так называемое среднеквадратичное приближение, для которого наименьшее значение имеет величина
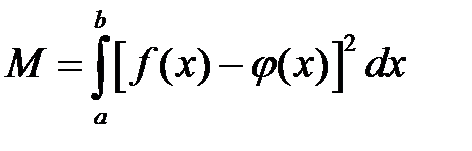
Потребовав обращения в нуль частных производных от М по параметрам, определяющим функцию j(x), получают уравнения, позволяющие найти наилучшие (в указанном смысле) значения этих параметров.
Точечная аппроксимация. Аппроксимация, при которой приближение строится на заданном дискретном множестве точек { xi }, называется точечной.
Для получения точечного среднеквадратичного приближения функции y=f(x), заданной таблично, аппроксимирующую функцию j(x) строят из условия минимума величины
,
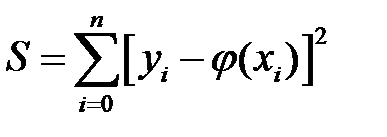где yi – значения функции f(x) в точках xi.
Основная сфера применения среднеквадратичного приближения – обработка экспериментальных данных (построение эмпирических формул).
Все виды аппроксимации представлены на рис.3.1, а возможные варианты аппроксимации и их определения на схеме 3.1.
Рис. 3.1
|
| ||||
   
| ||||
|
В данной лекции мы будем заниматься интерполированием, т.е. таким видом аппроксимации при котором аппроксимирующая функция принимает в заданных точках xi, те же значения yi, что и функция f(x), т.е.
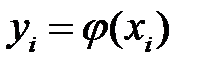, i =0, 1,…. n.
В этом случае, близость интерполирующей функции к заданной функции состоит в том, что их значения совпадают на заданной системе точек.
|
|
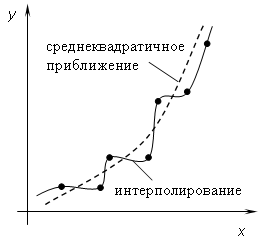Рис. 3.2
|
На рис. 3.2 показаны качественные графики интерполяционной функции (сплошная линия) и результаты среднеквадратичного приближения – т.е. аппроксимации (пунктирная линия). Точками отмечены табличные значения функции f(x).
Постановка задачи интерполирования. Пусть функция у = f(x) задана таблицей значений:
| x | x0 | x1 | … | xn |
| f (x) | y0 | y1 | … | yn |
Аппроксимирующую функцию j(x) будем строить таким образом, чтобы ее значения в точках { xi, i =0, 1,…. n } совпадали с табличными значениями заданной функции f(x):
. (3.1)
Такой способ введения аппроксимирующей функции называют лагранжевой интерполяцией, а условия (3.1) – условиями Лагранжа. Аппроксимирующая функция j(x), удовлетворяющая условиям Лагранжа, называется интерполяционной функцией. Значения { xi, i =0, 1,…. n } в данном контексте называют узлами интерполяции.
Задача интерполяции состоит в нахождение приближенных значений табличной функции при аргументах x, не совпадающих с узловыми, путем вычисления значений интерполяционной функции j(x). Если значение аргумента расположено внутри интервала [ x0, xn ], то нахождение приближенного значения функции f(x) называют интерполяцией, если аппроксимирующую функцию вычисляют вне интервала [ x0, xn ], то процесс называют экстраполяцией. Происхождение этих терминов связано с латинскими словами: inter – между, внутри, extra – вне, pole – узел.
Интерполяция степенным многочленом (полиномом). Известно, что через 
точек на плоскости можно провести кривую, являющуюся графиком степенного многочлена (полинома) степени n, причем такой полином единственный. Например, через две точки на плоскости можно провести только одну единственную прямую, т.е. полином первой степени, через три точки – параболу – полином второй степени и т.д. Этот факт лежит в основе полиномиальной интерполяции, при которой функцию j(x) строят в виде полинома степени n. Если на всем интервале интерполяции [ x0, xn ], содержащем n +1 узлов, строят один полином степени n, то говорят о глобальной интерполяции. Если интервал интерполяции [ x0, xn ], разбивают на меньшие отрезки, содержащие два или более узлов, и на каждом из отрезков строят свой (локальный) интерполяционный полином соответствующей степени, то говорят о локальной или многоинтервальной интерполяции.
Полином в каноническом виде. Выберем в качестве аппроксимирующей функции j(x) полином степени n в каноническом виде
. (3.2)
Коэффициенты полинома ci определяются из условий Лагранжа:
i =0, 1,…. n,
что с учетом выражения (3.2) дает систему уравнений с n+ 1 неизвестными:
(3.3)
Систему уравнений (3.3) можно кратко записать следующим образом
i =0, 1,…. n (3.3а)
или в матричной форме
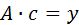, (3.3б)
где с – вектор–столбец, содержащий неизвестные коэффициенты ci, y – вектор–столбец, составленный из табличных значений функции yi, а матрица A имеет вид
.
Система линейных алгебраических уравнений (3.3) относительно неизвестных ci будет иметь решение, если определитель системы (определитель матрицы А) отличен от нуля. Определитель матрицы А, известный в алгебре как определитель Вандермонда, имеет аналитическое выражение:
.
Из этого выражения видно, что условие существования и единственности решения, 
, выполнено, если среди узлов xi нет совпадающих. Формально решение системы уравнений (3.3) может быть записано в матричном виде:
,
где A–1 – обратная матрица.
Глобальная интерполяция в пакете Mathcad легко реализуется самостоятельно, используя интерполяционные полиномы. На рис.3.3 приведен пример построение полинома в каноническом виде (3.2). Для этого, по заданным табличным данным (вектора X и Y) строится матрица А и находится вектор коэффициентов интерполяции – с – путем решения СЛАУ, записанного в виде (3.3б).
 Рис.3.3 Глобальная интерполяция в Mathcad.
|
На самом деле, в Mathcad, конечно, есть функции, позволяющие определить коэффициенты глобального полинома. Это функция
Polycoeff(х,у),
где х и у – таблично заданные данные.
В продолжение программы, приведенной на рис.3.3 можно написать программу, приведенную на рис.3.3а. Первая строка программы вычисляет коэффициенты глобального полинома (S) и сравнивает их с коэффициентами, полученными из решения СЛАУ (с). Вторая функция
Polyint(vx, vy, x)
реализует вычисление значения глобального полинома для таблично заданной функции (vx, vy) в точке х. Неудобство этой функции в том, что polyint возвращает вектор из двух элементов. В первом элементе содержится вычисленное значение, а во втором элементе – погрешность в точке вычисления.
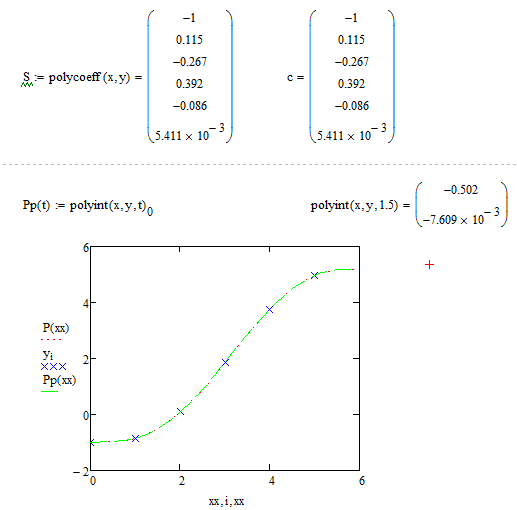 Рис.3.3а. Глобальная интерполяция в Mathcad(продолжение).
|
Еще одна функция,
polyiter(vx,vy,x,N,ε)
позволяет задать значение допустимой погрешности ε и максимальную степень полинома N, таким образом, с её помощью можно выполнять полиномиальную интерполяцию более низких степеней, снижая тем самым погрешность глобальной интерполяции. Возвращает вектор, в котором в 0 и 1 строках содержится служебная информация, а результат работы приведен во 2-й строке. Пример использования данной функции в сравнении с результатами интерполяции, выполненной ранее, приведен на рис.3.3.б.
Рис.3.3б. Глобальная интерполяция в Mathcad(продолжение).
Погрешность глобальной интерполяции. Ошибка приближения функции f (x) интерполяционным полиномом n –й степени Pn (x) в точке x определяется разностью:
. (3.4)
Можно показать, что погрешность Rn (x) определяется следующим выражением:
. (3.5)
Здесь 
– производная (n +1) порядка функции f (x) в некоторой точке 
, а функция ωn(x) определена как:
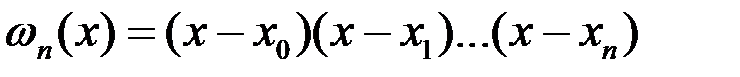(3.6)
Если максимальное значение производной 
равно
,
то для погрешности интерполяции следует оценка
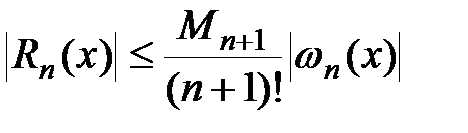. (3.7)
Конкретная величина погрешности в точке x зависит, очевидно, от значения функции ωn(x) в этой точке.
Качественный характер зависимости ωn(x) показан на рис. 3.4.
Рис. 3.4. Погрешность глобальной интерполяции
|
Из рис.3.4 видно, что погрешность интерполяции тем выше, чем ближе точка x лежит к концам отрезка 
. За пределами отрезка интерполяции (т.е. при экстраполяции) 
быстро растет, поэтому погрешность возрастает существенно.
Вследствие описанного поведения погрешности, глобальная интерполяция в некоторых случаях может давать совершенно неудовлетворительный результат.
Такого рода ситуацию в 1901 году обнаружил К. Рунге. Он строил на отрезке [–1,1] интерполяционные полиномы с равномерным расположением узлов для функции 
. Оказалось, что при увеличении степени интерполяционного полинома его значения сильно отклоняются от точных значений функции для любой точки x при 0.7< x <1.
В качестве примера на рис 3.5 приведены результаты интерполяции функции полиномом 8–й степени. Пунктирной линией показан график исходной функции, сплошная линия показывает график интерполяционного полинома, построенного по заданным точкам.
Рис. 3.5. Интерполяция функции  полиномом 8–й степени
|
В некоторых случаях удается улучшить результаты глобальной интерполяции за счет специального расположения узлов интерполяции (если они не зафиксированы). Доказано, что если функция f (x) имеет непрерывную производную на отрезке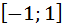 
, то при выборе значений xi, совпадающих с корнями полинома Чебышева степени n, интерполяционные полиномы степени n –1 сходятся к значениям функции в любой точке этого отрезка. Корни многочлена Чебышева 1 рода на отрезке 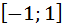, расположены неравномерно на отрезке и сгущаются к его концам. Такое сгущение компенсирует увеличение погрешности интерполяции при приближении к концам отрезка, которое имеет место при равномерном расположении узлов.
Многочлен Чебышёва первого рода Tn (x) характеризуется 
как многочлен степени n со старшим коэффициентом 2 n – 1, который меньше всего отклоняется от нуля на интервале [−1,1]. 
Многочлен Чебышёва второго рода Un (x) характеризуется как многочлен степени n со старшим коэффициентом 2 n, интеграл от абсолютной величины которого по интервалу [−1,1] принимает наименьшее возможное значение: 
.
Однако не всегда удается выбрать такое специальное расположение узлов, которое обеспечивает хорошую точность глобальной интерполяции. В тех случаях, когда узлы интерполяции фиксированы, уменьшение погрешности интерполяции осуществляют за счет уменьшения степени интерполяционных полиномов, применяя многоинтервальную интерполяцию.
Многоинтервальная интерполяция. Как было отмечено выше, глобальная интерполяция не всегда дает удовлетворительные результаты. Несмотря на выполнение условий Лагранжа в узлах, интерполяционная функция может иметь значительное отклонение от аппроксимируемой кривой между узлами. С увеличением количества узлов возрастает и степень интерполяционного полинома, что может приводить к увеличению погрешности в результате возникновения так называемого явления волнистости. Для того чтобы избежать высокой степени полинома отрезок интерполяции разбивают на несколько частей, и на каждом частичном интервале строят самостоятельный (локальный) полином невысокой степени. Ниже рассматриваются наиболее часто используемые виды многоинтервальной интерполяции, реализованные в Mathcad.
Кусочно–линейная интерполяция. Кусочно–линейная интерполяция является простейшим видом многоинтервальной интерполяции, при которой исходная функция на каждом частичном интервале 
аппроксимируется отрезком прямой, соединяющим точки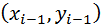 
и 
:
. (3.8)
При использовании кусочно–линейной интерполяции сначала нужно определить интервал, в который попадает значение аргумента x, а затем подставить его в формулу (3.8). Для случая равноотстоящих узлов 
номер интервала i, в который попадает значение аргумента, можно определить следующим образом
,
где int (x) – целая часть аргумента x.
Встроенная функция linterp(vx, vy, x) осуществляет кусочно–линейную интерполяцию. Аргументами этой функции являются два вектора vx и vy, содержащие исходные данные и независимая переменная x. пример использования этой функции приведен на рис. 3.6.
 Рис. 3.6
|
Сплайн–интерполяция. Существенным недостатком кусочно-линейной интерполяции является то, что в точках стыка разных интерполяционных полиномов оказывается разрывной их первая производная (функция имеет излом). Этот недостаток устраняется при использовании особого вида многоинтервальной интерполяции – интерполяции сплайнами (англ. spline – рейка, линейка).
Сплайн – это функция, которая на каждом частичном интервале представляется полиномом некоторой степени, и на всем отрезке интерполяции непрерывна вместе с несколькими своими производными. На практике широкое применение получили сплайны третьей степени (кубические сплайны).
На интервале кубический сплайн можно представить в следующем виде
, (3.9)
где 
– коэффициенты сплайнов; 
– номер сплайна (интервала).
Для определения коэффициентов сплайнов на всех n элементарных отрезках необходимо получить 4 n уравнений. Часть из них вытекает из так называемых условий сшивания соседних сплайнов в узловых точках:
1) равенство значений сплайнов s (x) и аппроксимируемой функции в узлах – условия Лагранжа, т.е. 
. Эти условия можно записать в виде:
,
, 
. (3.10)
2) непрерывность первой и второй производной сплайнов в узлах
, 
, 
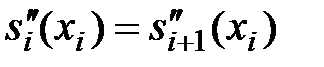(3.11)
Подставляя выражение (3.9) в (3.11) получаем 2n–2 уравнений
,
. (3.12)
Недостающие два соотношения получаются из условий закрепления концов сплайна.
В частности, при свободном закреплении концов можно приравнять нулю кривизну линии в этих точках. Такая функция, называемая свободным кубическим сплайном, обладает свойством минимальной кривизны, т. Е. она самая гладкая среди всех интерполяционных функций данного класса. Из условий нулевой кривизны на концах следуют равенства нулю вторых производных в этих точках:
, 
. (3.13)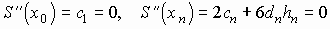 
Дополнительные условия могут быть и иными, поскольку их выбор, в общем случае, зависит от конкретной задачи.
Подстановка выражения (3.9) в (3.13) дает
, 
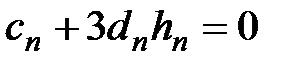. (3.14)
Соотношения (3.10), (3.12) и (3.14) дают полную систему из 4 n линейных алгебраических уравнений относительно коэффициентов сплайнов . На практике эту систему преобразуют к виду с трехдиагональной матрицей и решают методом прогонки.
Интерполяция сплайнами имеет очень простое и наглядное физико–механическое обоснование. Если попытаться совместить упругую металлическую линейку (или тонкий стержень) с узловыми точками, то форма, которую примет в этом случае линейка между соседними узлами будет совпадать с графиком кубического сплайна (сплошная линия на рис. 5). С физической точки зрения линейка принимает форму, при которой оказывается минимальной её потенциальная энергия. Из курса сопротивления материалов известно, что при этом форма линейки будет описываться уравнением вида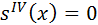 
. Откуда следует, что между каждой парой соседних узлов функция s (x) является полиномом степени не выше третьей. Вне узловых точек, где линейка свободна, она описывается уравнением прямой. Соответствующее поведение сплайна обеспечивается условием (3.13), в связи с чем, его иногда называют “условием свободных концов сплайнов”. Если к свободным концам линейки подвесить небольшие грузы, то линейка деформируется (пунктирная линия на рис. 3.7) и ее поведение вне узловых точек может быть описано, например, уравнением параболы. В этом случае условия (3.13) будут совершенно иными (“условия нагруженных сплайнов”).
|
lspline(vx, vy), pspline(vx, vy), cspline(vx, vy) – функции, возвращающие коэффициенты сплайнов;
interp(vs, vx, vy, x) – функция, возвращающая значение сплайна в точке x по исходным векторам vx и vy и по коэффициентам сплайна vs.
Функции lspline, pspline и cspline отличаются граничными условиями, определяющими поведения сплайнов вне интервала интерполяции.
· функция lspline генерирует кривую сплайна, которая приближается к прямой линии в граничных точках;
· функция pspline генерирует кривую сплайна, которая приближается к параболе в граничных точках.
функция cspline генерирует кривую сплайна, которая может быть кубическим полиномом в граничных точках.
Пример использования и наглядная разница в работе трех вариантов функции кубической интерполяции показаны на рис.3.8.
 Рис. 3.8.
|
Вообще можно строить полиномы, не только проходящие через заданные точки, но и имеющие в них заданные касательные, например, интерполяционный многочлен Эрмита является одной из модификаций многочлена Лагранжа. При его построении требуется, чтобы в узлах xi совпадали с табличными данными не только его значения, но и их производные до некоторого порядка. В общем случае выражение для многочлена Эрмита очень громоздко, и пользоваться им на практике трудно. Поэтому ограничиваются лишь некоторыми простейшими случаями. Но для этих случаев встроенных функций в пакете Mathcad не предусмотрено, однако при необходимости их можно написать самостоятельно.
Заметим, что от интерполирующих функций можно вычислять производные и интегралы, используя вcтроенные возможности Mathcad. Пример такого использования приведен на рис. 3.9.
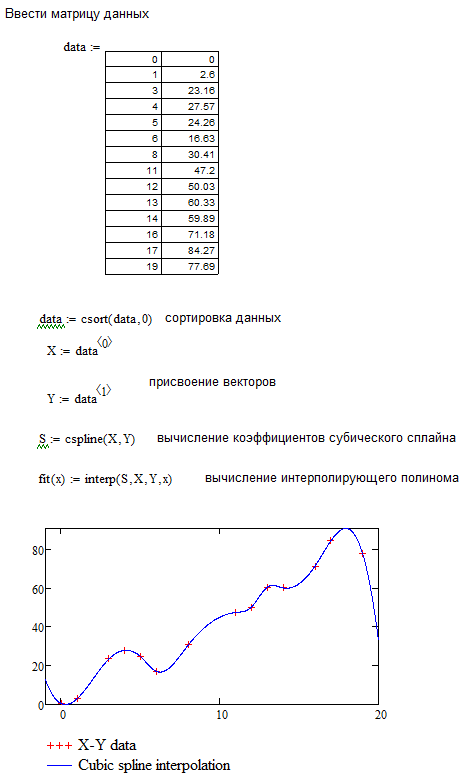Рис. 3.9
|
Рис. 3.9(продолжение)
|
Функции двух переменных. До сих пор рассматривалось интерполирование функций одной независимой переменной y = f (x). На практике возникает также необходимость построения интерполяционных формул для функций нескольких переменных. Для простоты ограничимся функцией двух переменных z = f (x, y).
Можно построить линейную интерполяционную формулу. Геометрически это означает, что нужно найти уравнение плоскости, проходящей через три заданные точки 
, где 
. В пакете Mathcad существуют встроенные функции для интерполяции функции двух переменных. Эти функции имеют тот же вид,что и для интерполяции функции одной переменной, только в качестве аргументов им передаются не вектора, а матрицы. Пример использования функции для линейной интерполяции приведен на рис. 3.10:
Рис. 3.10
Экстраполяция функций. Все рассмотренные выше функции осуществляли экстраполяцию данных за пределами их интервала с помощью соответствующей зависимости, основанной на анализе расположения нескольких исходных точек на границах интервала. В Mathcad имеется более развитый инструмент экстраполяции, который учитывает распределение данных вдоль всего интервала. В функцию predict встроен линейный алгоритм предсказания поведения функции, основанный на анализе, в том числе осцилляции.
predict (у, m, n) —
функция предсказания вектора, экстраполирующего выборку данных. Аргументы функции:
· у — вектор действительных значений, взятых через равные промежутки значений аргумента;
· m — количество последовательных элементов вектора у, согласно которым строится экстраполяция;
· n— количество элементов вектора предсказаний.
Пример использования функции предсказания на примере экстраполяции осциллирующих данных yi с меняющейся амплитудой приведен на рисунке. Там же, наряду с самой функцией, представлен полученный график экстраполяции. Аргументы и принцип действия функции predict отличаются от рассмотренных выше встроенных функций интерполяции–экстраполяции. Значений аргумента для данных не требуется, поскольку по определению функция действует на данные, идущие друг за другом с равномерным шагом. Пример использования этой функции приведен на рис.3.11.
Рис. 3.11. Работа функции predict для осциллирующей функции при большом числе исходных данных.
|
Как видно из рис.3.11, функция предсказания может быть полезна при экстраполяции данных на небольшие расстояния. Вдали от исходных данных результат часто бывает неудовлетворительным. Кроме того, функция predict хорошо работает в задачах анализа подробных данных с четко прослеживающейся закономерностью, в основном осциллирующего характера.
Если данных мало, то предсказание может оказаться бесполезным. На рис.3.12 приведена экстраполяция небольшой выборки данных. Соответствующий результат показан для различных крайних точек массива исходных данных, для которых строится экстраполяция.
 Рис.3.12 Работа функции предсказания в случае малого количества данных
|