Треугольник и окружность
Теория:
Окружность, описанная около треугольника
Окружность называют описанной около треугольника, если все вершины треугольника расположены на окружности.
Её центр равноудалён от всех вершин, то есть должен находиться в точке пересечения серединных перпендикуляров к сторонам треугольника.
Следовательно, около любого треугольника можно описать окружность, так как серединные перпендикуляры к сторонам пересекаются в одной точке.
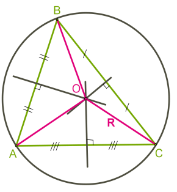
Для остроугольного треугольника центр окружности находится в треугольнике.
Другая ситуация с прямоугольным и тупоугольным треугольниками.
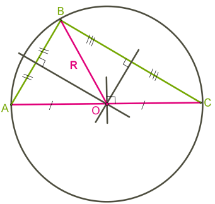

Окружность, вписанная в треугольник
Окружность называют вписанной в треугольник, если все стороны треугольника касаются окружности.
Её центр равноудалён от всех сторон, то есть должен находиться в точке пересечения биссектрис треугольника.
Следовательно, в любой треугольник можно вписать окружность, так как биссектрисы треугольника пересекаются в одной точке.
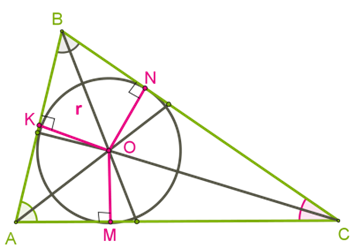
Так как биссектрисы углов треугольника всегда пересекаются внутри треугольника, то для всех треугольников центр вписанной окружности находится в треугольниках.
Формулы
Равносторонний треугольник
Обрати внимание!
У равностороннего треугольника совпадают биссектрисы, медианы и высоты, то есть, эти отрезки являются также серединными перпендикулярами. Это значит, что центры описанной и вписанной окружности совпадают.



Вписанная окружность в четырехугольник
Теория:
Если все стороны четырёхугольника касаются окружности, то он называется четырёхугольником, описанным около этой окружности, а окружность — вписанной в четырёхугольник.
Не все четырёхугольники возможно описать около окружности, так как биссектрисы четырёх углов могут не пересекаться в одной точке, и не удастся найти центр вписанной окружности.
Суммы противоположных сторон описанного четырёхугольника равны a+c=b+d.

Так как отрезки касательных, проведённых из одной точки к окружности, равны, и AB=AK+KB, BC=BL+LC, CD=CM+MD, и AD=DN+NA, то, очевидно, AB+CD=BC+AD.
Это свойство можно использовать и как признак для определения, в какие четырёхугольники можно вписать окружность.
Если суммы противоположных сторон четырёхугольника равны, то в такой четырёхугольник можно вписать окружность.
Самостоятельно сделай обзор четырёхугольников (параллелограмм, в том числе — квадрат, прямоугольник, ромб, трапеция, в том числе — равнобедренная трапеция и прямоугольная трапеция), в которые можно вписать окружность.
Вписанный четырёхугольник
Теория:
Четырёхугольник, все вершины которого лежат на окружности, называется вписанным в эту окружность, а окружность называется описанной около четырёхугольника.
Не все четырёхугольники возможно вписать в окружности, так как серединные перпендикуляры четырёх сторон могут не пересекаться в одной точке, и не удастся найти центр окружности, описанной около четырёхугольника.
Сумма противоположных углов вписанного четырёхугольника равна 180 градусам.

Все углы четырёхугольника являются вписанными в окружность, значит, равны половине дуг, на которые опираются. Противоположные углы опираются на дуги, которые вместе образуют окружность, то есть 360°. Следовательно, противоположные углы вместе образуют 180°.
Это свойство можно использовать и как признак для определения, около каких четырёхугольников можно описать окружность.
Если сумма противоположных углов четырёхугольника равна 180°, то около него можно описать окружность.
Самостоятельно сделай обзор четырёхугольников (параллелограмм, в том числе — квадрат, прямоугольник, ромб, трапеция, в том числе — равнобедренная трапеция и прямоугольная трапеция), около которых можно описать окружность.