IV. Аксиома непрерывности Дедекинда

Если все точки прямой как угодно разбить на два такие класса I и II, что любая точка класса II лежит правее любой I, то либо в классе I есть самая правая точка, и тогда в классе II нет самой левой, либо, наоборот, в классе II есть самая левая точка, и тогда в классе I нет самой правой.

Из аксиомы Дедекинда выводятся два фундаментальных предложения: постулат Архимеда и принцип Кантора. Их фундаментальность в том, что они есть основа теории измерений. Постулат Архимеда дает возможность поставить любому отрезку положительное число (длину отрезка) при заданной единице длины, принцип Кантора разрешает противоположную задачу – любому положительному числу устанавливает существование отрезка, для которого это число является длиной.

. Аксиома параллельности (аксиома Лобачевского.)

Существует такая прямая и точка 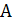, не лежащая на ней, что через точку А проходит не менее двух прямых, не пересекающих прямую а и лежащих с ней в одной плоскости [1, с.154-159].

Заметим, что существование хотя бы одной прямой, проходящей через данную точку и не пересекающей данной прямой, есть факт абсолютной геометрии. Аксиома Лобачевского утверждает существование по крайней мере двух таких прямых. Отсюда немедленно следует, что таких прямых существует бесконечное множество.

Рассмотрим доказательство непротиворечивости планиметрии Лобачевского на примере модели французского математика Анри Пуанкаре (1854 – 1912 гг.).

Для этого дадим интерпретацию следующих определений:

Плоскостью Лобачевского (Л-плоскостью) будем называть верхнюю евклидову полуплоскость, ограниченную прямой, носящей название абсолют, причём сама прямая исключается [5, c. 92-96].

Точками Лобачевского (Л-точками) будем называть евклидовы точки верхней полуплоскости, определяемой абсолютом, исключая точки, принадлежащие ему.

Прямыми Лобачевского будем называть евклидовы полуокружности верхней полуплоскости, ортогональные к абсолюту, т.е. имеющие центры на этой прямой, а также евклидовы полупрямые, перпендикулярные к абсолюту, с вершинами на этой прямой и расположенные в верхней полуплоскости.

Будем говорить, что «некоторая Л-точка инцидентна с некоторой Л-прямой» или что она «лежит» на этой Л-прямой, если соответствующей евклидовой полуокружности или полупрямой.

Два Л-отрезка будем называть конгруэнтными, если существует такая конечная последовательность инверсий с центрами на абсолюте, в результате которых соответствующая дуга АВ одной евклидовой полуокружности преобразуется в дугу CD другой.

Дадим определение понятию «лежать между». Пусть А, В, С – три Л – точки, лежащие на Л-прямой а. Будем говорить, что Л-точка С лежит между точками А и В на соответствующей полуокружности или полупрямой в обычном евклидовом смысле [4, c. 162-166].

Рассмотрим некоторую прямую в евклидовой плоскости.

Проверим выполнимости аксиом сочетания I_1-3.

Аксиомы I₁ и I₂ верны: если А и В 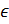верхней полуплоскости (Рисунок 1), значит, через них проходит либо единственная полуокружность с центром О на абсолюте, либо единственная полупрямая, перпендикулярная к абсолюту.

Аксиома I₃ имеет место, ведь на каждой полуокружности и полупрямой существует бесконечное множество точек и вне каждой из них существуют точки верхней полуплоскости.

Непротиворечивость аксиом II_1-3 имеют очевидна: они выполняются для точек полуокружности или полупрямой. Выполнимости аксиомы II₄ подтверждается следующим образом:

Рассмотрим уравнение окружности с центром на прямой XX при условии, что начало координат расположено на этой прямой и прямая XX принята за ось абсцисс. Пусть окружность g имеет центр О (а; 0) и радиус r:

. (1)

Можно показать, что для того, чтобы эта полуокружность пересекала дугу AB другой верхней полуокружности с центром на абсолюте во внутренней точке дуги, необходимо и достаточно, чтобы левая часть уравнения γ имела в точках A и B значения противоположных знаков.

Криволинейный ABC (рисунок 2), образованный дугами трех пересекающихся верхних полуокружностей, с центрами на абсолюте. Пусть некоторая четвертая полуокружность пересекает дугу AB во внутренней точке и не проходит через точки A, B и C, причём (1) есть уравнение этой четвёртой полуокружности. Тогда (для определенности), значит и В первом случае ( четвёртая полуокружность пересекает во внутренней точке дугу BC, во втором случае (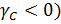 – дугу AC.

Проверим выполнимость аксиом конгруэнтности III_1-5.

Проверим выполнимость аксиомы III₁. Рассмотрим случай, когда отрезок AB и луч с началом в точке A изображаются дугами окружностей.

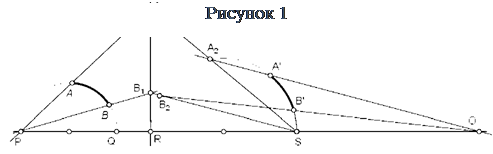Отрезок AB и луч с началом в точке A изображены на рисунке жирными линиями (рисунок 3). Рассмотрим цепь инверсий, переводящих отрезок AB в A B .

Сначала рассмотрим инверсию с центром в точке P, которая переводит точку Q в точку R. Так как окружность, на которой лежит отрезок AB, проходит через центр инверсии, она перейдет в прямую, перпендикулярную прямой PR и проходящую через точку R. Точки A и B перейдут в точки A₁ и B₁. Теперь рассмотрим инверсию с центром в точке S, для которой точка R будет инвариантной. Тогда прямая A₁B₁ перейдет в окружность с диаметром RS. Строим A₂ и B₂ – образы точек A₁ и B₁. Осталось отобразить инверсией точку A₂ в точку A . Тогда B₂ перейдет в искомую точку B . Получаем, что окружность с радиусом RS должны переходить в себя, а A₂ должна перейти в A . Такая инверсия существует (как мы видели выше) и ее центр будет пересечением прямых A₂A и RS. Получаем точку O и строим образ точки B₂, то есть точку B . Итак, мы построили отрезок A B , конгруэнтный отрезку AB на заданном луче.

Пятая группа аксиом состоит из одной аксиомы – аксиомы Лобачевского. V [4, c. 127-138].

Через точку, не лежащую на данной прямой проходит более одной прямой, не пересекающей данную.

Проиллюстрируем, что эта аксиома выполняется в модели Пуанкаре плоскости Лобачевского. На рисунке (рисунок 4) изображено несколько прямых, проходящих через точку A и не пересекающих прямую a.

Следовательно, аксиома Лобачевского в модели Пуанкаре выполняется. Обратим особое внимание на прямые b и e. Они выделяются среди других прямых, не пересекающих прямую a. Эти прямые называются параллельными прямой a. Строгое определение параллельных прямых на плоскости Лобачевского будет приведено чуть позже [1, с. 178-181].

Таким образом, мы установили, что при определении основных понятий планиметрии Лобачевского указанным выше образом выполняются все ее аксиомы. Следовательно, построена модель планиметрии Лобачевского в терминах евклидовой планиметрии.

Как мы уже отмечали, построение модели решает вопрос о непротиворечивости системы аксиом планиметрии Лобачевского условно: планиметрия Лобачевского непротиворечива постольку, поскольку непротиворечива планиметрия Евклида. В силу важности вывода повторим аргументацию еще раз, имея в виду уже построенную модель Пуанкаре.

Предположим, что в планиметрии Лобачевского имеют место две противоречащие одна другой теоремы. Пользуясь моделью Пуанкаре, мы можем сформулировать эти теоремы в терминах евклидовой геометрии. Получим два исключающих друг друга утверждения в евклидовой геометрии, то есть получим противоречие в геометрии Евклида.

Многие задачи геометрии Лобачевского проще решать в модели Пуанкаре, поскольку она построена на основе хорошо известной геометрии Евклида. В частности, в модели удобно выводить различные формулы геометрии Лобачевского.

Помимо А. Пуанкаре, «непротиворечивую» модель геометрии нашего соотечественника представил Феликс Клейн (1849 – 1925 гг.).

Литература:

1. Александров, П.С., Что такое неевклидова геометрия: учебное пособие / Александров П.С.; Издательство академии педагогических наук РСФСР; –М., 1950; – 72 с.

2. Каган, В.Ф., Лобачевский и его геометрия. / Каган В. Ф., Государственное издательство технико-теоретической литературы. – М.: ГИТТЛ, 1995. –303 с.

3. Каган, В.Ф., Лобачевский. / Каган В. Ф. –М.: Издательство Академии наук СССР; – 1944. –347 с.

4. Костин, В. И. Основания геометрии. / Костин В. И., Государственное учебно-педагогическое издательство министерства просвещения – М.: Учпедгиз, 1948. – 304 с.

5. Трайнин, Я.Л., Основания геометрии. / Трайнин Я. Л., Государственное учебно-педагогическое издательство министерства просвещения РСФСР – М.: Учпедгиз, 1961. – 325 с.