Рассмотрим идеи последовательных алгоритмов. Пусть дана схема электрических связей из множества элементов Е={e1…en}. Будем последовательно назначать элементы eiÎE (i=1,n) в куски Gi i = 1,l. На каждом шаге выбирается один из нераспределенных элементов и помещается в очередной кусок.
Кусок считается завершенным, если число элементов в узле равно заданному числу ni, либо назначение любого из нераспределенных элементов приводит к образованию такого числа связей куска, которое превышает предельно заданное.
После завершения формирования очередного куска, аналогично формируется следующий кусок, причем из элементов, не включенных в предыдущие узлы.
Тактика назначения элементов в куски в самом общем виде следующая:
1. на очередном шаге выделяются те элементы, включение каждого из которых в кусок не нарушает ограничений по числу элементов и выводов узла;
2. элементом, включенным в кусок на очередном шаге, является тот из элементов, выбранных на первом шаге, который имеет наибольшее число связей с элементами уже помещенными в узел. Если таких элементов несколько, то выбирается элемент, имеющий наименьшее число связей с нераспределенными элементами.
Имеется большое число алгоритмов, реализующих с теми или иными другими отличиями, этот общий характер процесса последовательного назначения.
Рассмотрим один из них.
Алгоритм 1 (последовательный алгоритм компоновки)
Пусть задан граф схемы G=(E,U), который необходимо разбить на l объектов G1,G2,…,Gl с числом вершин n1,n2,…,nl в кусках, Sni=n, i=1,l.
1. формируем первый кусок. В графе выбирается вершина eiÎE с максимальной степенью 
r(ei)=max. Если таких вершин несколько, то предпочтение отдается той вершине, которая имеет большее число кратных ребер, идущих к одной вершине. С вершины ei начинается построение куска G1;
2. в кусок G1 сначала включаем все вершины, смежные ei и саму эту вершину. Обозначим множество таких вершин Гei. Если количество вершин множества Гei равно n1, то кусок сформирован. Если число вершин больше n1, то удаляем «лишние» вершины, связанные с остающимися вершинами G меньшим числом ребер. Если мощность Гei меньше n1, то добавляем вершины из числа нераспределенных, имеющие наибольшее число связей с распределенными вершинами и наименьшее число связей с нераспределенными. Затем процесс повторяется для нового куска и т.д.
Описанный алгоритм достаточно прост и позволяет достаточно быстро получить результат. Однако, в общем случае он может привести к неэффективным результатам. Этот алгоритм наиболее эффективен для графа, в котором число вершин графа G значительно больше числа вершин в любом куске: n>>n1,n2,…,nl, поскольку существует много возможностей для выбора вершин.
Пример:
Пусть граф задан матрицей смежности
| R= | e1 | e 2 | e 3 | e 4 | e 5 | e 6 | e 7 | ||
| e1 | r(e1) = 5 | ||||||||
| e2 | r(e2) = 4 | ||||||||
| e3 | r(e3) = 6 | ||||||||
| e4 | r(e4) = 6 | ||||||||
| e5 | r(e5) = 8 | ||||||||
| e6 | r(e6) = 7 | ||||||||
| e7 | r(e7) = 6 |
Требуется разбить граф G на три куска по 3, 2, 2 вершины, т.е. n1=3,. n2=2, n3=3.
Выбираем вершину e5 с r(e5) = 8. Тогда Гe5={e5,e3,e4,e6,e7}.
n = 5 > n1=3. Нужно убрать 2 лишние вершины.
Для этого произведем условное удаление каждой вершины из Гe5 и подсчитаем число ребер zei, связывающих эту вершину с оставшимися вершинами Гe5.
При удалении e3 ze3=R35+R34+R36+R37=1+0+1+0=2
При удалении e4 ze4=R45+R34+R46+R47=1+0+4+0=5
При удалении e6 ze6=R65+R64+R36+R67=1+4+1+1=7
При удалении e7 ze7=R75+R74+R76+R73=5+0+1+0=6
Удаляем e3 (т.к. ze3 min) и получим Гe5={e5,e4,e6,e7}
Нужно удалить еще одну вершину.
При удалении e4 ze4=R45+R46+R47=1+4+0=5
При удалении e6 ze6=R65+R64+R67=1+4+1=6
При удалении e7 ze7=R75+R74+R76=5+0+1=6
Удаляем e4 (т.к. ze4 = min) и получим Гe5={e5,e6,e7}
3. Первый кусок сформирован. Из оставшихся вершин E*={e1,e2,e3,e4} формируем следующий кусок. Матрица смежности принимает вид.
| R = | e1 | e 2 | e 3 | e 4 | ||
| e1 | r(e1) = 5 | |||||
| e2 | r(e2) = 4 | |||||
| e3 | r(e3) = 4 | |||||
| e4 | r(e4) = 1 |
Выбираем вершину e1 с r(e1)=5. Тогда Гe1={e1,e2,e3}.
n = 3 > n1=2. Нужно убрать 1 лишнюю вершину.
Для этого произведем условное удаление каждой вершины из Гe1 и подсчитаем число ребер zei, связывающих эту вершину с оставшимися вершинами Гe1.
При удалении e1 ze1=R12+R13=2 +3=5
При удалении e2 ze2=R21+R23=2+1=3
При удалении e3 ze3=R31+R32=3+1=4
Удаляем e2 (т.к. ze2 = min) и получим Гe1 = {e1,e3}
Гe1=(e1,e3) - кусок сформирован.
Т.к. остались всего две вершины, то третий кусок будет содержать вершины e2, и e4: Гe2={e2,e4}.
Результат разбиения графа G на три куска: Гe5={e5,e6,e7}, Гe1={e1,e3}, Гe2={e2,e4}. Онприведен на рис. 3.2.
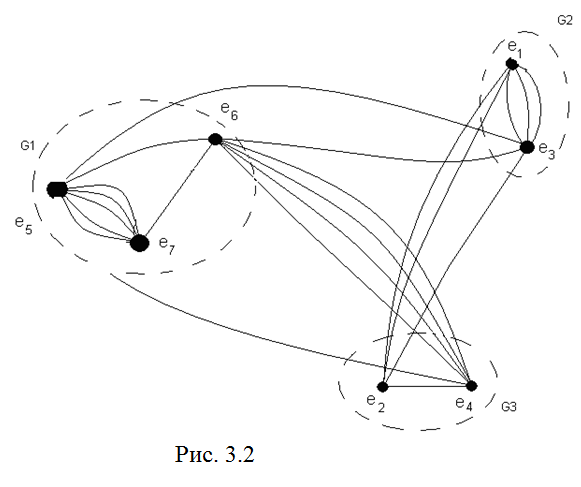
Число соединительных ребер всех кусков графа к равно 10.
Суммарное число внутренних ребер (ребер подмножеств Ui) равно 11.
Коэффициент разбиения DG=11/10=1.1.
Есть другой вариант алгоритма, при котором первой вершиной первого куска берется вершина с наименьшей степенью.
Провести разбиение по этому варианту самостоятельно и сравнить результаты.
Оглавление
Лекция 3. 1
Решение задачи компоновки конструктивных узлов. 1
Постановка задачи разбиения электрических схем (компоновки) 1
Алгоритмы разбиения графов. 7
Последовательные алгоритмы.. 8
Алгоритм 1 (последовательный алгоритм компоновки) 9