Лекция 3
Решение задачи компоновки конструктивных узлов
Постановка задачи разбиения электрических схем (компоновки)
Повторим материал из лекции 1.
При решении задач конструкторского проектирования можно условно выделить этапы:
· ввод и контроль информации;
· построение формальной модели схемы, т.е. разбиение электрической схемы на конструктивно законченные части - компоновка;
· размещение;
· трассировка;
· выдача конструкторской документации.
Из всего комплекса задач технического проектирования самой важной является задача разбиения электрических схем на конструктивно законченные части.
Электрооборудование всегда содержит иерархию конструктивных частей.
При проектировании конструктивных узлов можно выделить уровни:
1. микросхема, электрорадиоэлемент, модуль;
2. типовой элемент замены (ТЭЗ) – включает в себя элементы уровня 1;
3. панель – состоит из типовых элементов замены;
4. рама – конструктивный уровень, в который входят панели; 
5. стойки – собираются из элементов уровня 4, тумбы, пульты – собираются из элементов уровня 3.
Компоновкой (разбиением) электрической схемы на конструктивно законченные части называется процесс распределения элементов низшего конструктивного уровня в высший в соответствии с выбранным критерием.
Наиболее приемлемым критерием является критерий минимизации числа соединений между конструктивными узлами, т.к. он дает уменьшение массы изделий, минимизирует взаимные наводки, увеличивает надежность, упрощает конструкцию. В связи с этим рассмотрение методов компоновки электрических схем будет проводиться в основном на примере критерия минимума числа соединений между конструктивными узлами.
|
|
Этот критерий принимается за основной, остальные включаются в ограничения.
Исходной для решения задачи компоновки ЭО является электрическая схема соединений. Для алгоритмизации и формального решения задачи производится переход от электрической схемы соединений ЭО к графу, мультиграфу, к гиперграфу одним из рассмотренных выше методов.
Вспомним определение.
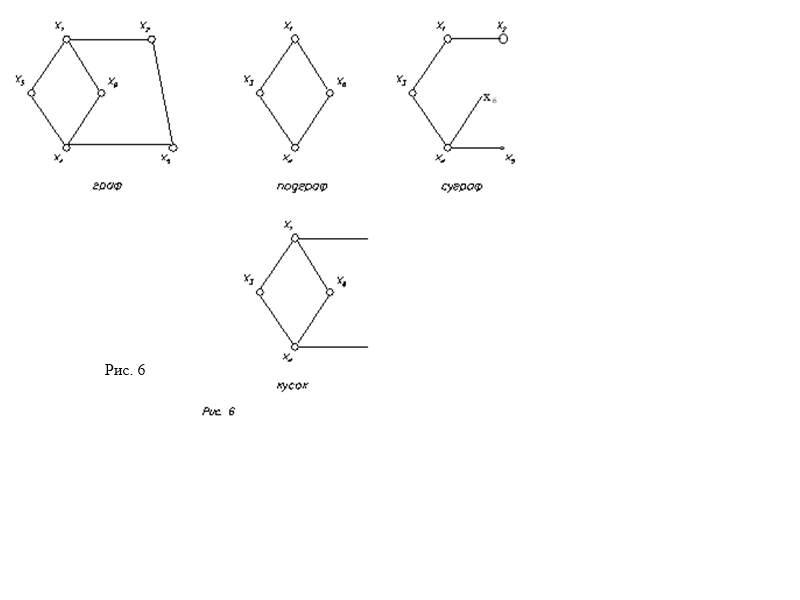
 Кусок графа G(Z,U) – это граф Q(X,Y), являющийся частью исходного графа такой, что X — подмножество Z, а в Y входят все ребра из U, инцидентные X.
Кусок графа G(Z,U) – это граф Q(X,Y), являющийся частью исходного графа такой, что X — подмножество Z, а в Y входят все ребра из U, инцидентные X.
Сформулируем задачу разбиения схемы как задачу разбиения графа G=(E, U) на куски Gi=(Ei,Ui), ЕiÍЕ, UiÍU, iÎI ={1,2,…,l}, где l – число кусков.
Совокупность Р(G) называется разбиением графа G(E,U), если:
| " GiÎР(G) [Gi ≠ Ø], iÎI "Gi, "GjÎР(G) [Gi≠Gj → Ei∩Ej=Ø & (Ui∩Uj=Ø v Ui∩Uj=Uij)] ÈG i=G | (4.1) |
Другими словами: совокупность кусков Р(G)={G1…Gl} является разбиением графа, если:
- любой кусок из этих совокупностей не пустой;
- для любых двух кусков из Р(G) пересечение множества вершин пусто;
- пересечение множества ребер может быть не пустым;
- объединение всех кусков в точности равно исходному графу G.
Множество Uij определяет подмножество ребер Uij≤U, попадающих в разрез между кусками Gi и Gj графа G.
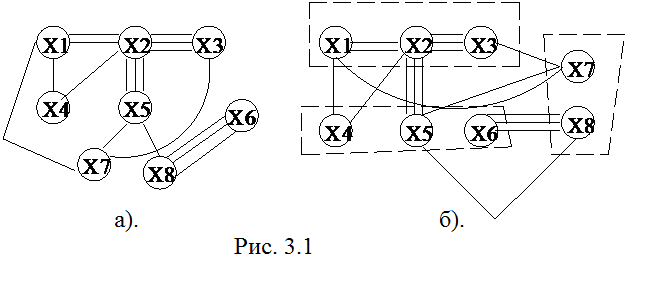
На рис. 3.1,а приведен граф G, содержащий 8 вершин и 17 ребер. Одно из возможных разбиений графа G на три куска показано на рис. 3.1,б.
Обозначим │Uij│= kij и назовем его числом соединительных ребер кусков Gi и Gj графов. Число соединительных ребер всех кусков графа
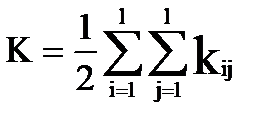 , i ≠ j , i ≠ j
| (3.2) |
В рассмотренном примере К=12.
|
|
Задачей разбиения графа G(E,U ) является нахождение такой совокупности частей, при которой число соединительных ребер графа удовлетворяло бы заданному критерию оптимальности.
Пусть граф G(E,U ) разбит на l кусков G1, G2,…,Gl. Тогда множество ребер U графа G можно представить в виде:
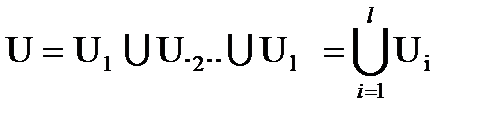
| (3.3) |
где
| U1=U1,1ÈU1,2È…ÈU1,l U2=U2,1ÈU2,2È…ÈU2,l …… …………………. Ui=Ui,1ÈUi,2È… ÈUi,l … ……………………. U1=Ul,1È Ul,2È…ÈUl,l | (3.4) |
где:
- Ui – подмножество всех ребер, инцидентных вершинам Ei куска Gi;
- Ui,i – подмножество ребер, соединяющих подмножество вершин Ei куска Gi между собой;
- Ui,j – подмножество ребер, соединяющих куски Gi и Gj.
Назовем коэффициентом разбиения ∆(G) графа G отношение суммарного числа внутренних ребер (ребер подмножеств Ui,i) к суммарному числу соединяющих ребер Ui,j.
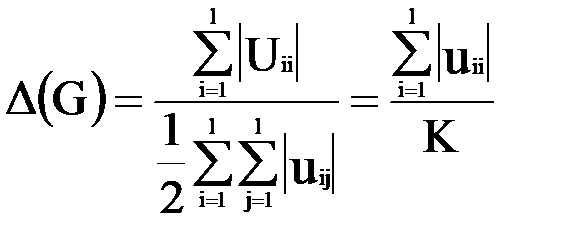
| (3.5) |
Коэффициент ∆(G) служит для оценки разбиения графа G на куски. Для графа на рис. 3.1 ∆(G)= 5/12.
Этот коэффициент можно также использовать как критерий для сравнения различных алгоритмов разбиения графа. Оптимальным разбиениям для оного и того же графа соответствуют наибольшие значения ∆(G).
Задача разбиения графа G на куски относится к задачам комбинаторно-логического типа, получение оптимального решения которых связано с большим перебором различных вариантов разбиения.
Алгоритмы разбиения графов
Существует большое количество алгоритмов разбиения графа, которые условно можно подразделять на следующие группы:
1. последовательные алгоритмы разбиения;
2. итерационные алгоритмы;
3. алгоритмы, основанные на приемах целочисленного программирования, например, на методе ветвей и границ;
|
|
4. алгоритмы, основанные на решении задачи о назначении;
5. смешанные алгоритмы.