МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное автономное бюджетное образовательное учреждение
Высшего образования
«Севастопольский государственный университет»
Методические указания
к лабораторному занятию по курсу
«Параллельные и распределенные вычисления»
на тему:
«ПЛАНИРОВАНИЕ ЗАДАНИЙ ДЛЯ
МУЛЬТИПРОЦЕССОРНЫХ СИСТЕМ»
Севастополь
«УТВЕРЖДАЮ»
Заведующий кафедрой ИТиКС
А.А. Брюховецкий
 |
«» 2018 г.
 |  |
ЛАБОРАТОРНОЕ ЗАНЯТИЕ № 1
по курсу «Параллельные и распределенные вычисления» на тему:
«ПЛАНИРОВАНИЕ ЗАДАНИЙ
ДЛЯ МУЛЬТИПРОЦЕССОРНЫХ СИСТЕМ»
Цель работы:
1. Закрепление и углубление теоретических знаний.
2. Привитие умения использовать алгоритмы планирования заданий для мультипроцессорных систем по критерию минимизации числа процессоров, необходимых для завершения пакета заданий за фиксированное время Т0.
3. Развитие и закрепление интереса обучаемых к преподаваемому предмету.
ПЛАН ЗАНЯТИЯ
1. Вводная часть 05 мин.
2. Основная часть 70 мин
а) решение задачи по алгоритму FF 15 мин
б) решение задачи по алгоритму FFD 10 мин
в) решение задачи по алгоритму BF 15 мин
г) решение задачи по алгоритму BFD 10 мин
д) самостоятельная работа 20 мин
е) выполнение заданий лабораторной работы 180 мин
3. Заключительная часть 05 мин
В результате проведения занятия студенты должны
ЗНАТЬ:
1. Основные методы планирования заданий в мультипроцессорных системах.
2. Критерии, используемые при планировании заданий.
УМЕТЬ:
Планировать задания по критерию минимизации числа процессоров, необходимых для завершения пакета заданий за фиксированное время Т0.
ЛИТЕРАТУРА:
1. Гудман С., Хидетниеми С. Введение в разработку и анализ алгоритмов. - М.: Мир, 1981. - 368с.
2. Конспект лекций по ПиРВ.
Краткие теоретические сведения.
Задача планирования заданий J1,..., JM для вычислительной системы, содержащей процессоры Р1 ,..., РN эквивалентна следующей задаче упаковки. Пусть каждому процессору Рj соответствует ящик Вj размера Т0. Каждому заданию Ji соответствует предмет размера ti, равного времени выполнения задания Ji, i=1,…, n. Теперь для решения задачи по составлению плана обработки пакета заданий нужно построить алгоритм, позволяющий разместить все предметы в минимальном количестве ящиков. Ящики нельзя заполнить сверх их объема Т0 и предметы нельзя дробить на части.
Рассмотрим множество предметов L={3, 3, 2, 2, 2}. На рис. 1 представлено оптимальное размещение этих предметов в минимальном количестве ящиков размера 4, где заштрихованные участки обозначают пустые места в ящиках.
|
|

|



 4
4
Рисунок 1.
Для решения задачи существуют следующие эвристические алгоритмы:
1. FF (First Fit) – первое попавшееся размещение для заданного списка.
2. FFD (First Fit Decreasing) – первое попавшееся размещение с убыванием.
3. BF (Best Fit) – лучшее размещение для заданного списка.
4. BFD (Best Fit Decreasing) – лучшее размещение с убыванием.
2.Тестовые примеры.
2.1 Решить задачу планирования заданий по алгоритму FF.
Т0 (В)=1000. Найти минимальное количество процессоров, необходимых для выполнения следующей последовательности заданий
L =(379, 395, 760, 379, 241, 200, 105, 40, 395, 105)
Первый предмет из L кладем в ящик В1. Второй предмет из L кладем в В1, если он туда помещается. В противном случае кладем его в следующий ящик В2. Вообще очередной предмет из L кладем в ящик Вi, куда этот предмет поместиться, причем индекс i ящика наименьший среди всех возможных. Если предмет не помещается ни в один из К частично заполненных ящиков, кладем его в ящик ВК+1. Этот основной шаг повторяется, пока список L не будет исчерпан.
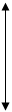
|
|
B1 B2 B3 B4
 | |||||
 | |||||
 | |||||
 | |||||


 1000
1000
2.2 Решить задачу планирования заданий по алгоритму FFD.
Т0 (В)=1000. Найти минимальное количество процессоров, необходимых для выполнения следующей последовательности заданий
L =(379, 395, 760, 379, 241, 200, 105, 40, 395, 105)
Этот алгоритм отличается от алгоритма FF тем, что список L упорядочен от больших предметов к меньшим.
L =(760, 395, 395, 379, 379, 241, 200, 105, 105, 40)
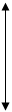 Реализовав этот алгоритм получим решение: min к-во процессоров = 3.
Реализовав этот алгоритм получим решение: min к-во процессоров = 3.








2.3 Решить задачу планирования заданий по алгоритму BF.
Т0 (В)=13. Найти минимальное количество процессоров, необходимых для выполнения следующей последовательности заданий
L =(7, 9, 7, 1, 6, 2, 4, 3).
Пусть L – заданный порядок заданий. Основной шаг тот же, что и в FF, но очередной предмет кладется в тот ящик, где остается наименьшее неиспользованное пространство. Таким образом, если очередной предмет имеет размер 3 и есть четыре частично заполненных ящика размера 6, в которых осталось 2, 3, 4 и 5 единиц незаполненного пространства, тогда предмет кладется во второй ящик, и тот становится полностью заполненным.
Реализовав этот алгоритм, получим решение: min к-во процессоров = 4.
B1 B2 B3 B4
 |  |
| |||||||
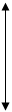 | |||||||||
 13
13


 |
2.4 Решить задачу определения минимального количества процессоров по алгоритму BFD, использовав список заданий L предыдущей задачи.
Алгоритм BFD такой же, как и BF, но L упорядочен от больших предметов к меньшим.