ГОУ ВПО Кубанский государственный технологический университет
(КубГТУ)
Кафедра автоматизации производственных процессов
Факультет Компьютерных технологий и автоматизированных
ванных систем
Пугачев В.И.
ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Конспект лекций по разделам дисциплины «Цифровые и стохастические системы управления»
Для студентов заочной и МИПС форм обучения специальности 220201 – Управление и информатика в технических системах
Краснодар,
Издательство КубГТУ,
Конспект лекций / В.И. Пугачев. Кубан. гос. Техн.Ун-т. Краснодар, 2005. - 100с.
УДК 62-50.007.07
Теория автоматического управления
(раздел «Цифровые и стохастические системы управления»)
Приведены сведения об основных методах, используемых при решении задач цифрового управления и стохастической динамики систем
Ил. 24 Библиогр.: 5 назв.
Печатается по решению Редакционно-издательского совета КубГТУ
Рецензенты:
канд.техн.наук, заместитель директора по науке, зав. лабораторией
автоматизации Кубанского филиала
“ ВНИЗ” Ю.Ф. Марков,
канд.техн.наук, профессор КубГТУ
З.Г. Насибов
Кубанский государственный технологический университет, 2005 г.
| Содержание | ||
| Цифровые системы управления | ||
| 1.1 | Способ управления с помощью ЭВМ. | |
| 1.2 | Решетчатые функции и разностные уравнения | |
| 1.3 | Условие устойчивости линейных цифровых систем, писанных разностными уравнениями | |
| 1.4 | Дискретное преобразование Лапласа | |
| 1.5 | Определение периода квантования при дискретном измерении без потери информации непрерывного сигнала | |
| 1.6 | Основные свойства 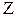 -преобразования -преобразования
| |
| 1.7 | Дискретная передаточная функция. | |
| 1.8 | Получение оригинала из уравнений в конечных разностях и с помощью 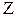 -преобразования -преобразования
| |
| 1.9 | Цифровые аналоги типовых законов управления | |
| 1.10 | Анализ цифровых систем управления | |
| 1.11 | Анализ устойчивости цифровых систем | |
| 1.12 | Аналитический синтез алгоритма управления цифрового вычислительного устройства | |
| 1.13 | Алгоритм цифрового управления по критерию быстродействия | |
| 1.14 | Особенности реализации цифровых законов управления в системах с сервомотором постоянной скорости | |
| Статистическая динамика | ||
| 2.1 | Основные задачи статистической динамики | |
| 2.2 | Характеристики случайных процессов | |
| 2.3 | Стационарные случайные процессы | |
| 2.4 | Основные свойства корреляционной функции и спектральной плотности стационарных случайных процессов | |
| 2.5 | Прохождение случайных воздействий через линейную САУ | |
| 2.6 | Анализ систем регулирования при стационарных случайных воздействиях | |
| 2.7 | Синтез САУ при заданной структуре | |
| 2.8 | Фильтр Винера - Колмогорова | |
| Литература | ||
| Приложение |
1 ЦИФРОВЫЕ СИСТЕМЫУПРАВЛЕНИЯ
Преимущества цифровых регуляторов в сравнении с непрерывными заключаются в том, что один цифровой регулятор может заменить несколько аналоговых а так же реализовать дополнительные функции проверки номинальных режимов, подстройку параметров регулятора по разомкнутому циклу, обмен информацией с другими регуляторами, взаимное резервирование, диагностика, выбор управляющих алгоритмов, реализацию адаптивных законов управления.
В отличие от непрерывных регуляторов законы регулирования здесь реализуются в форме алгоритмов, запрограммированных с помощью аппаратных или программных средств, обрабатываются дискретные по времени сигналы, причем сами сигналы квантованы по амплитуде в аналого-цифровых и цифро-аналоговых (АЦП и ЦАП) преобразователях и в центральном процессоре.
Благодаря гибкости средств программного обеспечения выбор законов управления не ограничивается только стандартными звеньями П, И или 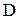 - типов. Кроме того, цифровые системы обладают повышенной чувствительностью, большей надежностью, отсутствием дрейфа, повышенной помехоустойчивостью, меньшими габаритами и массой, удобством в программировании.
- типов. Кроме того, цифровые системы обладают повышенной чувствительностью, большей надежностью, отсутствием дрейфа, повышенной помехоустойчивостью, меньшими габаритами и массой, удобством в программировании.
1.1 Способ управления с помощью ЭВМ
Элементная схема цифровой системы управления изображена на рисунке 1.1.
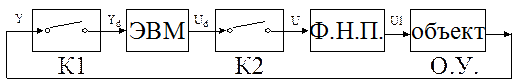
Рисунок 1.1 - Элементная схема цифровой САУ
Здесь:
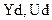 - дискретные значения на входе и выходе ЭВМ;
- дискретные значения на входе и выходе ЭВМ;
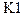 - квантователь, совмещенный с аналого-цифровым преобразователем;
- квантователь, совмещенный с аналого-цифровым преобразователем;
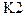 - квантователь, совмещенный с цифроаналоговым преобразователем;
- квантователь, совмещенный с цифроаналоговым преобразователем;
ЭВМ - устройство, реализующее алгоритм управления;
Ф.Н.П.- фиксатор нулевого порядка (или экстраполятор 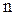 -того порядка);
-того порядка);
О.У. - объект управления.
Квантование по времени осуществляется квантователем 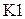 с определенным периодом
с определенным периодом 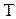 . Непрерывная регулируемая величина "
. Непрерывная регулируемая величина " 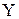 " преобразуется в дискретную "
" преобразуется в дискретную " 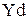 ", которая поступает в центральный процессор ЭВМ. Здесь она обрабатывается по запрограммированным алгоритмам и формируется управляющее воздействие. Если исполнительное устройство аналоговое, то данные поступают на квантователь
", которая поступает в центральный процессор ЭВМ. Здесь она обрабатывается по запрограммированным алгоритмам и формируется управляющее воздействие. Если исполнительное устройство аналоговое, то данные поступают на квантователь 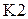 с цифро-аналоговым преобразователем, выход которого поступает на фиксатор нулевого порядка. Сигнал с фиксатора поступает на исполнительный механизм, перемещающий регулирующий орган и, следовательно, изменяющий выходную величину объекта управления "
с цифро-аналоговым преобразователем, выход которого поступает на фиксатор нулевого порядка. Сигнал с фиксатора поступает на исполнительный механизм, перемещающий регулирующий орган и, следовательно, изменяющий выходную величину объекта управления " 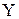 ".
".
Строго говоря, замыкание ключей на входе и выходе системы происходит не одновременно. Эта задержка равна времени, затрачиваемому на преобразование аналоговой информации в цифровую и последующую ее обработку в процессоре. Однако, поскольку это время мало в сравнении с постоянными времени сервомотора, объекта, измерителя, то им пренебрегают, полагая, что входные и выходные квантователи действуют синхронно. Кроме того, в АЦП, имеющих не менее 10 двоичных разрядов, эффекты квантования по уровню практически незаметны и в первом приближении можно считать амплитуды дискретных сигналов изменяются непрерывно.
Устройство фиксации управляющего сигнала задерживает его на постоянном уровне до появления следующего. Во временной области его выходной сигнал можно записать как реакцию на единичное входное импульсное воздействие в виде: K(t)=1(t)-1(t-T). (1.1)
Поскольку преобразование Лапласа мгновенного импульса единичной площади равно единице, то изображение импульсной переходной функции формирующего элемента равно передаточной функции этого элемента. 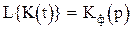 .
.
Прямое преобразование Лапласа функции (1.1) имеет вид:
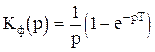 . (1.2)
. (1.2)
Анализ цифровых систем упрощается, если вместо непрерывного времени 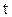 ввести относительное
ввести относительное 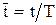 .
.
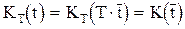 .
.
По определению прямое преобразование Лапласа
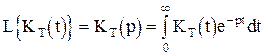 .
.
Аналогично можно записать
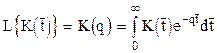 .
.
Используя свойство прямого преобразования Лапласа об изменении масштаба, получим:
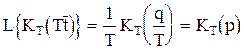 . (1.3)
. (1.3)
Таким образом, для получения передаточной функции в относительном масштабе времени по передаточной функции от непрерывной необходимо аргумент " 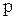 " заменить на
" заменить на 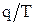 и результат умножить на
и результат умножить на 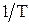 . При этом умножение производится один раз для всей приведенной непрерывной части системы.
. При этом умножение производится один раз для всей приведенной непрерывной части системы.
Использование дискретных моментов времени или относительного масштаба времени при исследовании цифровых систем управления приводит к необходимости применения решетчатых функций, разностных уравнений и связанного с ними дискретного преобразования Лапласа.
1.2 Решетчатые функции и разностные уравнения
Решетчатой называется функция, которую образуют ординаты непрерывной функции 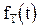 , соответствующие дискретным равноотстоящим друг от друга значениям независимой переменной, рисунок 1.2. Она равна нулю, когда
, соответствующие дискретным равноотстоящим друг от друга значениям независимой переменной, рисунок 1.2. Она равна нулю, когда 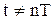 и обозначается
и обозначается 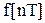 ;
;
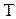 - период дискретности;
- период дискретности; 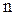 - любое целое число.
- любое целое число.
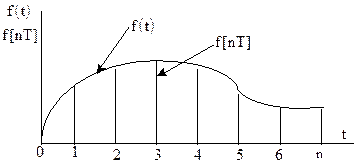
Рисунок 1.2 - Вид непрерывной и решетчатой функции
Для выявления поведения непрерывной функции между дискретными моментами вводят промежуточное фиксированное время 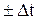 , которое может изменяться от
, которое может изменяться от 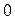 до
до 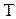 .
.
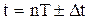
Такая функция называется смещенной.
Использовав относительное время, решетчатую функцию запишем 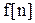 , или
, или 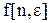 , где
, где 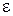 может изменяться в пределах от
может изменяться в пределах от 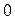 до
до 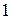 .
.
Скорость изменения решетчатой функции 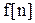 характеризуется ее первой разностью:
характеризуется ее первой разностью:
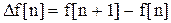 .
.
Разность второго порядка, или вторая разность
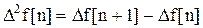 ,
,
или
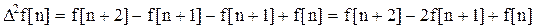 .
.
Разность 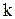 -того порядка определяется выражением
-того порядка определяется выражением
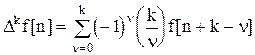 , (1.4)
, (1.4)
где 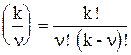 - биномиальные коэффициенты.
- биномиальные коэффициенты.
При рассмотрении цифровых систем используются разностные уравнения, определяющие соотношения между дискретной функцией 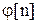 и ее разностями различных порядков
и ее разностями различных порядков 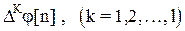 . Их можно записать так:
. Их можно записать так:
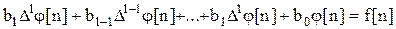 ,
,
или
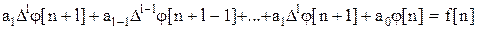 ,
,
где 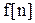 - известная дискретная функция.
- известная дискретная функция.
При воздействии на линейную часть прямоугольных импульсов, имеющих разрывы, интегрирование возможно проводить для линейных уравнений только в промежутках времени, где разрывы отсутствуют. Это связано с тем, что наличие разрывов приводит к изменению постоянных интегрирования, которые определяются два раза за период. Этот метод построения переходного процесса является слишком громоздким и возможен для конкретных цифровых расчетов, исключающих анализ и синтез в общем виде.
Применение разностных уравнений позволяет избежать указанных недостатков. Рассмотрим методику получения уравнений в конечных разностях.
Разностное уравнение характеризует связь между переменными, разделенными целым числом периодов. Для возможности проведения анализа всей системы необходимо иметь все уравнения динамики в одной форме (например, в виде разностных уравнений). Найдем уравнение объекта в виде разностного уравнения. Для этого решим дифференциальное уравнение объекта
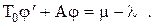 (1.5)
(1.5)
Пусть 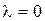 ,
,
тогда 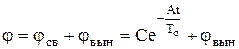 ;
; 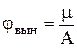 ;
; 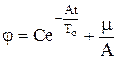 .
.
Постоянную интегрирования 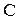 найдем из граничных условий в начале и конце периода.
найдем из граничных условий в начале и конце периода.
При 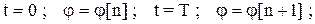

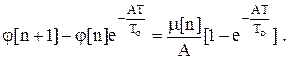 (1.6)
(1.6)
В итоге получили разностное уравнение (1.6).
При решении системы разностных уравнений возникает необходимость исключения промежуточных переменных. Это удобно выполнять оперативным методом. С этой целью каждую переменную представим в виде 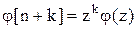 ,
,
где 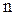 - номер наименьшего периода.
- номер наименьшего периода.
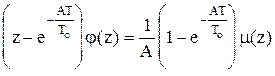 .
.
В итоге получили алгебраическое уравнение.
При физической реализации алгоритмов управления используются левые конечные разности. Познакомимся с ними в процессе получения уравнения в конечных разностях для дифференциального уравнения второго порядка. Наиболее простым способом получения уравнений в конечных разностях по дифференциальным является метод замены производных соответствующими разностями.
В рассматриваемом случае порядок, дифференциальных уравнений второй, поэтому используя соотношения:
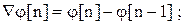
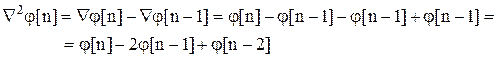 (1.7)
(1.7)
Дифференциальное уравнение можно записать через конечные разности, например:
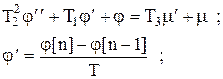
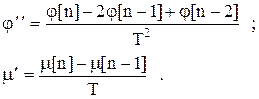
Подставив значения 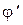 ,
, 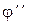 ,
, 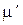 , получим:
, получим:
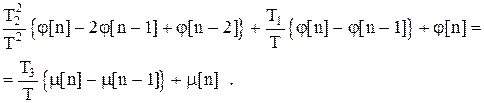
Приведя подобные члены и сделав обозначения:
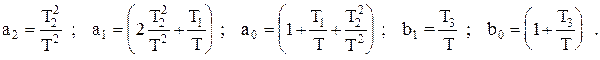
получаем
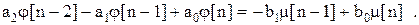 (1.8)
(1.8)
Второй метод получения уравнений в конечных разностях приближенный. Он тем точнее, чем меньше 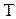 . Для уравнения (1.5) при использовании второго метода легко получить уравнение в конечных разностях, которое имеет вид
. Для уравнения (1.5) при использовании второго метода легко получить уравнение в конечных разностях, которое имеет вид
 (1.9)
(1.9)
Если сравнить выражение (1.6) и (1.9), то мы увидим, что они отличаются друг от друга, поскольку (1.9) является приближенным, а (1.6) - точным. Приближенность (1.9) объясняется тем, что мы фактически используем для решения исходного дифференциального уравнения численный метод интегрирования.
Если разложить коэффициенты при 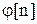 и
и 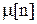 выражения (1.6) в ряд Маклорена и удержать только два первых члена, то
выражения (1.6) в ряд Маклорена и удержать только два первых члена, то
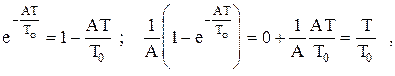
т.е. коэффициенты (1.9) являются первым приближением коэффициентов (1.6) при разложении их в ряд Маклорена в окрестности точки 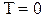 .
.
Второй способ более универсален, поскольку не требует знания правой части дифференциального уравнения и его решения.
Решение разностных уравнений
Линейные импульсные системы описываются линейными разностными уравнениями с постоянными коэффициентами. Они подчиняются принципу суперпозиции, поэтому их полное решение состоит из суммы решений однородного и неоднородного уравнения.
Пусть дано однородное уравнение
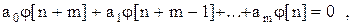
где 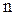 - номер текущего периода (аналог времени
- номер текущего периода (аналог времени 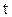 );
);
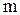 - порядок разностного уравнения.
- порядок разностного уравнения.
Составим характеристическое уравнение, введя оператор
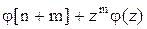 ,
,
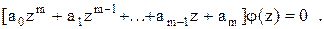
Отсюда характеристическое уравнение принимает вид
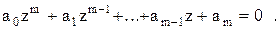
Решение однородного уравнения находим в виде
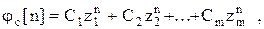 (1.10)
(1.10)
где 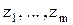 - корни характеристического уравнения.
- корни характеристического уравнения.
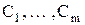 - постоянные коэффициенты, определяемые по начальным условиям для решения неоднородного уравнения.
- постоянные коэффициенты, определяемые по начальным условиям для решения неоднородного уравнения.
Если 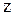 имеет
имеет 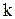 -тую кратность, то решение запишем в виде
-тую кратность, то решение запишем в виде
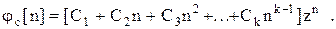
Частное решение неоднородного разностного уравнения находим в форме правой части (аналогично обыкновенным дифференциальным уравнениям).
Если  - правая часть, то, когда
- правая часть, то, когда 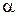 не совпадает ни с одним корнем, частное решение записывается в виде
не совпадает ни с одним корнем, частное решение записывается в виде
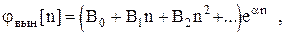
если 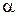 совпадает с одним из корней кратности "
совпадает с одним из корней кратности " 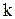 " то
" то
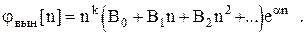
1.3 Условие устойчивости линейных импульсных систем, описанных разностными уравнениями
Для устойчивой импульсной системы должно выполняться условие
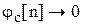 при
при 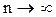 ,
,
где 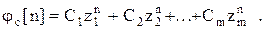
Для того чтобы 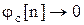 необходимо, чтобы каждое слагаемое при
необходимо, чтобы каждое слагаемое при 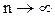 стремилось к нулю. Это условие будет выполнено, если
стремилось к нулю. Это условие будет выполнено, если 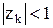 ,
,
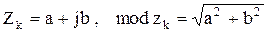 , поэтому
, поэтому
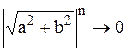 при
при 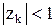 и
и 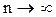 .
.
На комплексной плоскости корни характеристического уравнения должны располагаться внутри единичного круга, рисунок 1.7.
Если 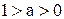 , то процесс будет монотонным затухающим, если
, то процесс будет монотонным затухающим, если 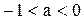 , то процесс будет колебательным.
, то процесс будет колебательным.
Если 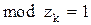 , то система находится на границе устойчивости.
, то система находится на границе устойчивости.
Если 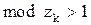 , то система неустойчива.
, то система неустойчива.
Алгебраический критерий устойчивости импульсных
систем
С помощью замены переменных (дробно-линейного преобразования 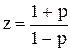 можно отобразить поверхность единичного круга в плоскости
можно отобразить поверхность единичного круга в плоскости 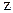 в левую полуплоскость комплексного переменного
в левую полуплоскость комплексного переменного 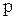 .
.
Такое преобразование называется конформным.
Пусть 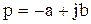 , тогда покажем, что
, тогда покажем, что 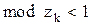 .
.
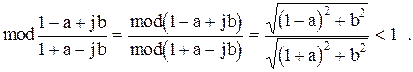
Сделав в характеристическом уравнении замену переменных 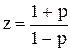 , получим новое характеристическое уравнение, к которому применимы критерии устойчивости Гурвица и Михайлова. Если эти критерии выполняются, то импульсная система устойчива.
, получим новое характеристическое уравнение, к которому применимы критерии устойчивости Гурвица и Михайлова. Если эти критерии выполняются, то импульсная система устойчива.
Частотный критерий устойчивости импульсных систем,
описываемых разностными уравнениями
Пусть дано характеристическое уравнение импульсной системы 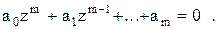
Если известны его корни, то характеристическое уравнение можно переписать в виде
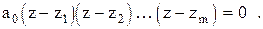
В критерии Михайлова осуществлялась замена в характеристическом уравнении 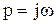 , т.е., вектор
, т.е., вектор 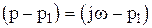 скользил по границе устойчивости. Поскольку границей устойчивости импульсных систем является круг единичного радиуса, то произведем замену
скользил по границе устойчивости. Поскольку границей устойчивости импульсных систем является круг единичного радиуса, то произведем замену
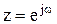 ,
,
где 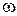 - угол
- угол 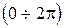 , а не частота.
, а не частота.
Приращение аргумента функции
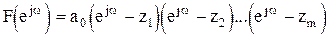
равно
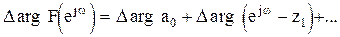 (1.11)
(1.11)
1. 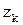 - внутри единичного круга, рисунок 1.3.
- внутри единичного круга, рисунок 1.3.
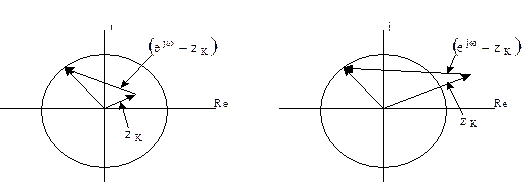
Рисунок 1.3 - Расположение корней характеристического уравнения
В этом случае
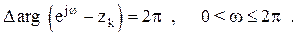
2. 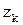 - снаружи единичного круга, рисунок 1.3,б. В этом случае
- снаружи единичного круга, рисунок 1.3,б. В этом случае
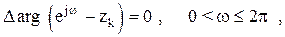
следовательно, CAP устойчива, если годограф 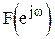 последовательно проходит против часовой стрелки
последовательно проходит против часовой стрелки 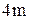 квадрантов при изменении
квадрантов при изменении 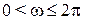 .
.
Если
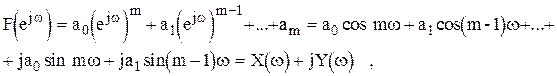
где 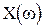 - четная функция, то, следовательно,
- четная функция, то, следовательно, 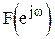 - симметричная относительно действительной оси комплексной плоскости. Это говорит о том, что достаточно изменять
- симметричная относительно действительной оси комплексной плоскости. Это говорит о том, что достаточно изменять 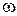 в пределах
в пределах 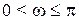 . Поэтому импульсная система будет устойчива, если годограф
. Поэтому импульсная система будет устойчива, если годограф 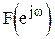 начинается на вещественней полуоси и поворачивается против часовой стрелки на угол
начинается на вещественней полуоси и поворачивается против часовой стрелки на угол 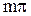 при изменении
при изменении 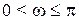 ,
,
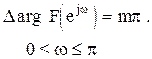 (1.12)
(1.12)
На рисунке 1.4 показаны годографы 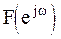 для устойчивых систем первого, второго и третьего порядка.
для устойчивых систем первого, второго и третьего порядка.
1.4 Дискретное преобразование Лапласа
Решетчатая функция 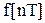 получается при модуляции последовательности мгновенных импульсов единичной площади
получается при модуляции последовательности мгновенных импульсов единичной площади 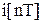 с периодом повторения
с периодом повторения 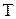 сигналом
сигналом 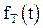 .
.
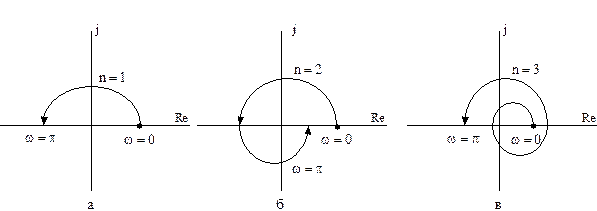
Рисунок 1.4 - Виды годографов устойчивых систем
Действие амплитудно-импульсного модулятора сводится к перемножению 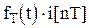 , поэтому
, поэтому
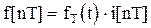 , (1.13)
, (1.13)
где 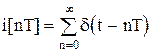 ,
, 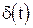 - функция Дирака.
- функция Дирака.
Поэтому
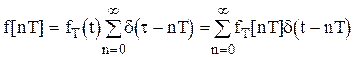 ,
,
так как перемножение происходит только в моменты 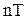 .
.
Изображение по Лапласу элементарного 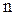 -того импульса
-того импульса 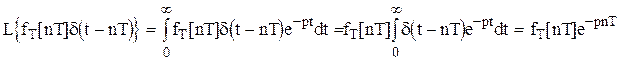 .
.
Преобразование последовательности импульсов представим в виде
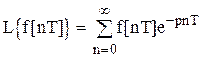 . (1.14)
. (1.14)
Изображение решетчатой функции по Лапласу называется дискретным преобразованием Лапласа.
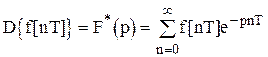 .
.
Для случая, когда в качестве аргумента берется относительное время 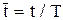 , выражение для
, выражение для 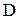 -преобразования принимает вид
-преобразования принимает вид
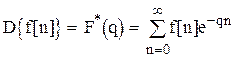 , (1.15)
, (1.15)
где 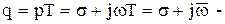
параметр дискретного преобразования Лапласа, 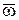 - относительная частота
- относительная частота 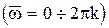 .
.
Метод, предложенный Я.3.Цыпкиным, позволяет как и при анализе непрерывных систем ввести понятия о передаточных и частотных функциях, а также о частотных характеристиках импульсных систем.
Для смещенной расчетной функции
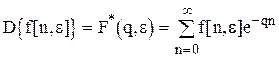 . (1.16)
. (1.16)
Например, 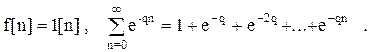
Предел этого ряда - сумма бесконечной геометрической прогрессии
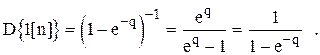 (1.17)
(1.17)
Оператору " 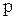 " можно в дискретном преобразовании поставить в соответствие выражение
" можно в дискретном преобразовании поставить в соответствие выражение 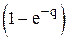 .
.
Поскольку изображение решетчатой функции зависит от 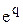 , то функция
, то функция 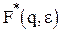 на комплексной плоскости переменной
на комплексной плоскости переменной 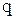 будет периодической вдоль мнимой оси
будет периодической вдоль мнимой оси
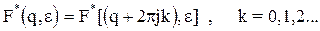 (1.18)
(1.18)
Оригинал решетчатой функции может быть найден с помощью обратного преобразователя Лапласа
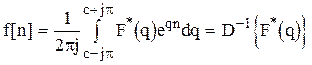 . (1.19)
. (1.19)
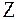 -преобразование - можно рассматривать как модификацию дискретного преобразования Лапласа, использующего подстановку
-преобразование - можно рассматривать как модификацию дискретного преобразования Лапласа, использующего подстановку 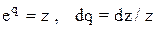 .
.
Формула 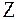 -преобразования получит вид
-преобразования получит вид
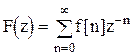 . (1.20)
. (1.20)
Для обратного преобразования
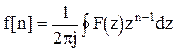 . (1.21)
. (1.21)
Такая модификация приводит к тому, что изображение 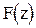 становится функцией переменной
становится функцией переменной 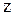 , а область устойчивости характеризуется единичным кругом на комплексной плоскости
, а область устойчивости характеризуется единичным кругом на комплексной плоскости 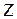 ,
, 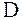 и
и 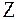 -преобразования являются совершенно эквивалентными.
-преобразования являются совершенно эквивалентными.
1.5 Определение периода квантования при дискретном измерении без потери информации непрерывного сигнала
Решетчатая функция может быть получена с помощью перемножения модулирующего сигнала 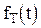 и последовательности равноотстоящих мгновенных импульсов единичной площади
и последовательности равноотстоящих мгновенных импульсов единичной площади 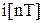 :
:
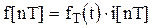 ,
,
где
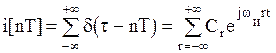 . (1.22)
. (1.22)
Здесь
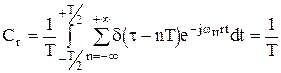 для любого
для любого 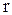 ,
, 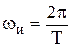 .
.
Дискретный сигнал запишем так:
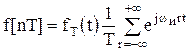 , (1.23)
, (1.23)
а его спектр можно выразить следующим образом:
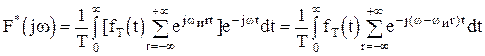 .(1.24)
.(1.24)
Изображение Фурье 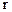 -того члена суммы (1.24) можно записать в виде
-того члена суммы (1.24) можно записать в виде
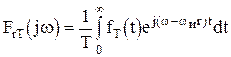 ;
;
или, применив теорему смещения параметра 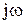 , получим
, получим
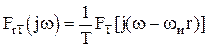 .
.
Если 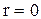 то
то 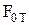
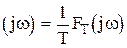 ,
,
т.е. частотный спектр первого члена суммы есть частотный спектр модулируемого сигнала.
Для 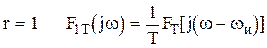 , т.е. частотный спектр второго члена суммы остается прежним, но сдвинутым в
, т.е. частотный спектр второго члена суммы остается прежним, но сдвинутым в
частотной области на величину 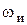 и т.д.
и т.д.
В итоге получим преобразование Фурье амплитудно-модулированной последовательности импульсов в виде суммы частотных спектров непрерывной функции, смещенных по оси частот на величину 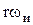 , где
, где 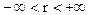 .
.
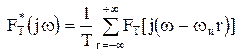 . (1.25)
. (1.25)
Это выражение справедливо, если 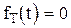 при
при 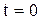 .
.
Если при 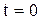
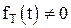 , то
, то
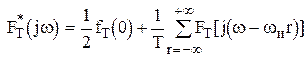 . (1.26)
. (1.26)
Заменив 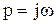 , в уравнении (1.26) получим связь преобразований Лапласа для решетчатой функции с преобразованием Лапласа для непрерывной функции
, в уравнении (1.26) получим связь преобразований Лапласа для решетчатой функции с преобразованием Лапласа для непрерывной функции
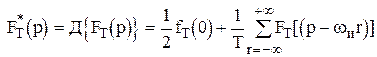 , (1.27)
, (1.27)
где 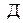 -преобразование и
-преобразование и 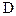 -преобразование связаны между собой
-преобразование связаны между собой
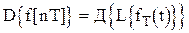 .
.
Если в качестве аргумента непрерывной функции принято относительное время, то соотношение (1.27) представим в виде
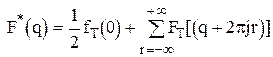 , (1.28)
, (1.28)
где 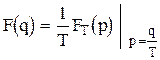 .
.
Из частотного представления решетчатой функции (1.26) вытекает теорема о дискретном представлении непрерывных функций. Она устанавливает связь между спектром непрерывной функции и частотой повторения импульсов, при которой возможно восстановление непрерывной функции.
В.А.Котельников доказал, что непрерывная функция может быть восстановлена без искажений, если частота повторения импульсов 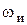 по крайней мере в два раза больше максимальной частоты
по крайней мере в два раза больше максимальной частоты 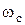 спектра этой непрерывной функции, рисунок 1.5.
спектра этой непрерывной функции, рисунок 1.5. 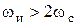 .
.
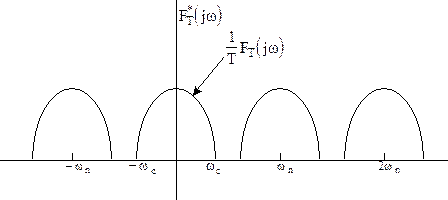
Рисунок 1.5 - Спектр решетчатой функции
1.6 Основные свойства 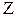 -преобразования
-преобразования
Как говорилось ранее, если в дискретном преобразовании Лапласа произвести замену 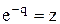 , то получим:
, то получим:
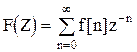 .
.
Это соотношение дает некоторые преимущества по сравнению с дискретным преобразованием (упрощается запись выражений, легче вычисляется обратное преобразование). При этом 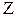 -преобразование обладает следующими свойствами.
-преобразование обладает следующими свойствами.
Линейность.
Если 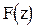 и
и 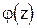
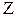 -преобразования решетчатых функций
-преобразования решетчатых функций 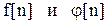 , то
, то
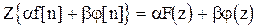 .
.
Действительно, 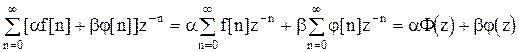 . (1.29)
. (1.29)
Опережение.
Пусть 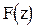
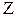 -преобразование решетчатой функции
-преобразование решетчатой функции 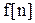 .
.
Тогда по определению
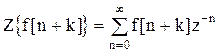 .
.
Умножив и разделив правую часть на 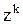 , получим:
, получим:
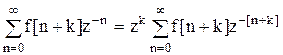 .
.
Обозначим 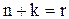 , тогда
, тогда
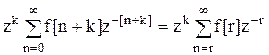 .
.
Для получения под знаком суммы полного ряда начиная с 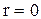 , прибавим и вычтем соответствующие слагаемые
, прибавим и вычтем соответствующие слагаемые
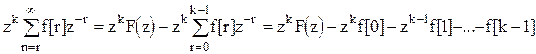 . (1.30)
. (1.30)
Для нулевых начальных условий
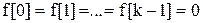 ,
,
поэтому
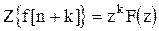 . (1.31)
. (1.31)
Свертка решетчатых функций.
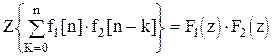 . (1.32)
. (1.32)
Изображение разностей.
На основании свойств о линейности и опережении можно записать:
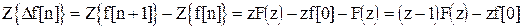 .
.
Для второй разности:
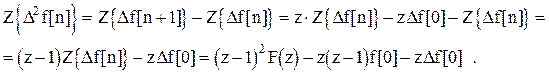
Продолжая дальнейшие вычисления разностей, можно заметить общую закономерность их получения:
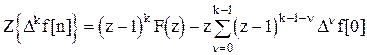 . (1.33)
. (1.33)
Для нулевых начальных условий
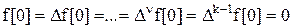
имеем:
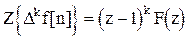 . (1.34)
. (1.34)
Дифференцирование изображения.
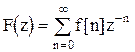 ;
;
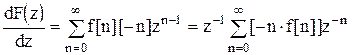 .
.
Умножив левую и правую часть равенства на 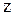 , получаем:
, получаем:
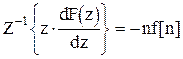 . (1.35)
. (1.35)
Умножение производной изображения на 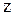 эквивалентно умножению оригинала на -
эквивалентно умножению оригинала на - 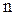 , Это позволяет легко получать изображения степенных функций.
, Это позволяет легко получать изображения степенных функций.
Например: 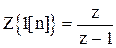 ;
;
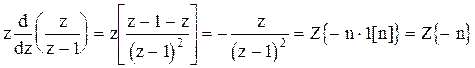 .
.
Начальное значение оригинала.
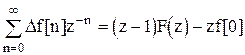 .
.
Умножим левую и правую части равенства на 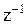 и устремим в бесконечность
и устремим в бесконечность 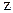 .
.
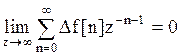 , поскольку
, поскольку 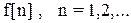 -конечные величины и
-конечные величины и 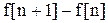 также конечны.
также конечны.
В итоге 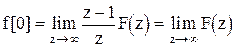 . (1.36)
. (1.36)
Конечное значение оригинала.
Используя изображение конечной разности, запишем:
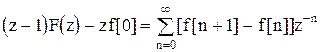 .
.
Умножим левую и правую части равенства на
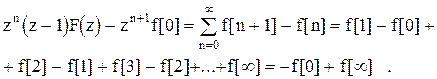
Устремив 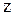 к единице, найдем:
к единице, найдем:
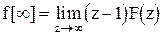 (1.37)
(1.37)
1.7 Дискретная передаточная функция
Если динамическая система описывается дифференциальным уравнением, то его можно представить уравнением в конечных разностях вида:
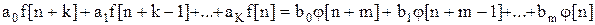 .
.
Используя теорему о смещении решетчатой функции в 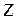 -преобразовании при нулевых начальных условиях получим:
-преобразовании при нулевых начальных условиях получим:
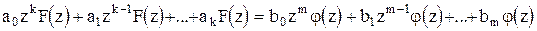 .
.
Отношение 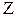 -преобразования выходной величины к
-преобразования выходной величины к 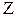 -преобразованию входной при нулевых начальных условиях называется дискретной передаточной функцией.
-преобразованию входной при нулевых начальных условиях называется дискретной передаточной функцией.
Для статических объектов коэффициент усиления можно найти используя теорему о конечном значении оригинала функции.
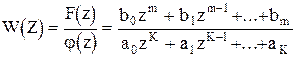 ; (1.38)
; (1.38)
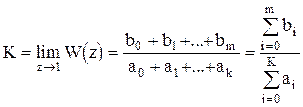 . (1.39)
. (1.39)
Для физической реализации алгоритмов вычисления значений решетчатой функции необходимо использовать левые разности, которые учитывают предыдущие а не последующие значения решетчатой функции при вычислении разностей.
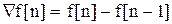 ;
;
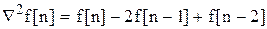 .
.
В этом случае передаточные функции будут полиномами 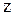 в отрицательных степенях. Если имеется
в отрицательных степенях. Если имеется