3.8.1. Задание полученных значений коэффициентов b0, a0-a3, d0- d3; с0-с2. Определение передаточной функции разомкнутой и замкнутой (по управлению и возмущению) САУ
%Расчет САУ%
%Ввод данных%
a_0=0.00000795;
a_1=0.056;
a_2=0.25;
a_3=14.46;
b_0=34.73;
d_0=0.00000795;
d_1=0.056;
d_2=0.25;
d_3=49.2;
c_0=0.00056;
c_1=3.98;
c_2=17.4;
Ia=29;
Uzad=441.71;
%Передаточная функция разомкнутой САУ по управлению%
n=[b_0];d=[a_0 a_1 a_2 a_3];Wraz=tf(n,d)
% Передаточная функция замкнутой системы САУ по управлению%
n=[b_0];d=[d_0 d_1 d_2 d_3];Wzam=tf(n,d)
%Переходный процесс по управлению%
t=[0:0.001:5];[y_1,t]=step(Wzam*Uzad,t);plot(t,y_1),grid;
%Передаточная функция замкнутой САУ по возмущению%
n=[c_0 c_1 c_2];d=[d_0 d_1 d_2 d_3];Wvoz=tf(n,d)
%Переходный процесс по возмущению%
t=[0:0.001:5];[y_2,t]=step(Wvoz*Ia,t);plot(t,y_2),grid;
figure(1);
SUBPLOT(2,1,1),plot(t,y_1),grid;
SUBPLOT(2,1,2),plot(t,y_2),grid;
Transfer function:
34.73
------------------------------------------
7.95e-006 s^3 + 0.056 s^2 + 0.25 s + 14.46
Transfer function:
34.73
-----------------------------------------
7.95e-006 s^3 + 0.056 s^2 + 0.25 s + 49.2
Transfer function:
0.00056 s^2 + 3.98 s + 17.4
-----------------------------------------
7.95e-006 s^3 + 0.056 s^2 + 0.25 s + 49.2
3.8.2. Определение нулей и полюсов замкнутой (по управлению и возмущению) САУ {команда: “zpk(Wzam)”}
%Нули и полюса замкнутой системы по управлению%
zpk(Wzam)
%Поле нулей и полюсов замкнутой системы по управлению%
[p,z]=pzmap(Wzam)
%Нули и полюса замкнутой системы по возмущению%
zpk(Wvoz)
%Поле нулей и полюсов замкнутой системы по возмущению%
[p,z]=pzmap(Wvoz)
Zero/pole/gain:
4368553.4591
--------------------------------
(s+7040) (s^2 + 4.342s + 879.1)
p =
1.0e+003 *
-7.0397
-0.0022 + 0.0296i
-0.0022 - 0.0296i
z = Empty matrix: 0-by-1
Zero/pole/gain:
70.4403 (s+7103) (s+4.375)
--------------------------------
(s+7040) (s^2 + 4.342s + 879.1)
p =
1.0e+003 *
-7.0397
-0.0022 + 0.0296i
-0.0022 - 0.0296i
z =
1.0e+003 *
-7.1028
-0.0044
Вывод:
Т.к. все корни меньше нуля и находятся в отрицательной полуплоскости, то можно сделать вывод о том, что исследуемая САУ устойчивая.
Определение полей нулей и полюсов замкнутой системы по управлению и возмущению
{команда: “[p,z]= pzmap(Wzam)”};

Рис. 16 – поле нулей и полюсов замкнутой системы по управлению и возмущению (Matlab)
3.8.4. Построение годографа Найквиста и вывод об устойчивости исходной системы {команда: “ nyquist(Wraz)”}
%Годограф Найквиста для разомкнутой системы%
nyquist(Wraz)
figure(1);
SUBPLOT(1,1,1), nyquist(Wraz);
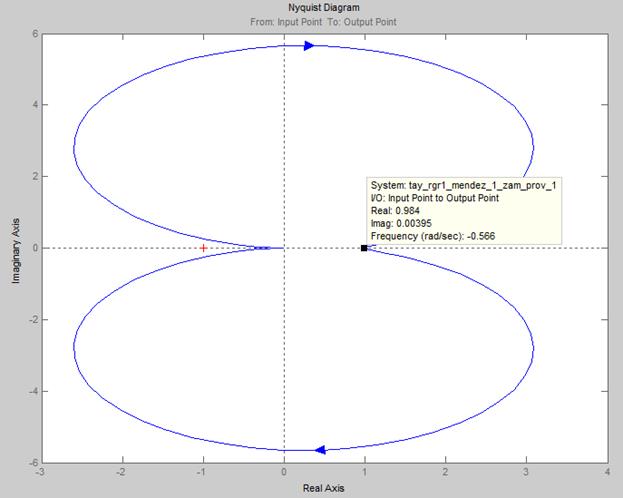
Рис. 17 – Моделирование системы ТП-Д по передаточной функции при помощи Matlab.
Диаграмма Найквиста.
Вывод:
Т.к. годограф Найквиста разомкнутой системы не охватывает точку «-1», то можно сделать вывод о том, что исследуемая САУ устойчивая.
3.8.5 определить характеристики Боде, частоты среза и автоколебаний { команда: “ margin(Wraz)”};
%Характеристика Боде для разомкнутой системы%
margin(Wraz)
figure(2);
SUBPLOT(1,1,1), margin(Wraz);
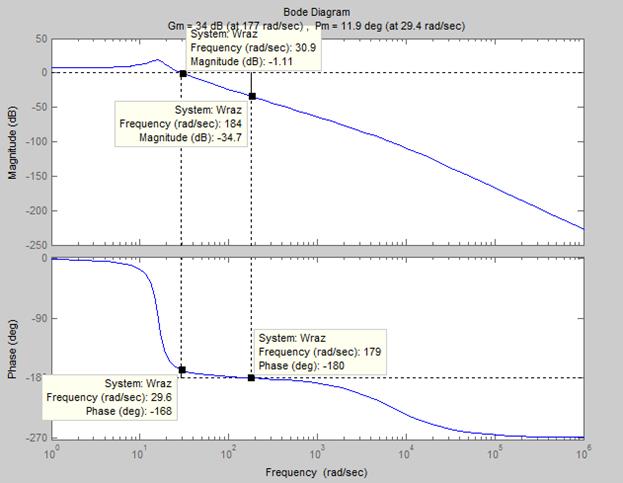
Рис. 18 – Характеристика Боде, частота среза и автоколебаний
3.8.6. График переходных процессов Ω=f(t),команды: t=[0: 0.001: 1]; [Ω,t]=step(Wzam*Uzad,t); plot(t,Ω),gridи t=[0: 0.001: 1]; [Ω,t]=step(Wraz*Ia,t); plot(t,Ω),grid.
%Переходный процесс по управлению%
t=[0:0.001: 3];[y_1,t]=step(Wzam*Uzad,t);plot(t,y_1),grid;
%Переходный процесс по возмущению%
t=[0:0.001:3];[y_2,t]=step(Wvoz*Ia,t);plot(t,y_2),grid;
figure(3);
SUBPLOT(2,1,1),plot(t,y_1),grid;
SUBPLOT(2,1,2),plot(t,y_2),grid;

Рис. 19 – переходные процессы по управлению и возмущению для замкнутой САУ
Исходя из формы переходных процессов по графикам рис.19, можно сделать вывод, при возмущающем воздействии САУ необходимо больше времени, чтобы перейти в устойчивое состояние.
Моделирование САУ в SIMULINK
Моделирование по схеме и по передаточной функции. Сравнение графиков переходных процессов

Рис. 20 - схема САУ ТП-Д, сравнение результатов моделирования в симулинк и расчётной передаточной функции системы
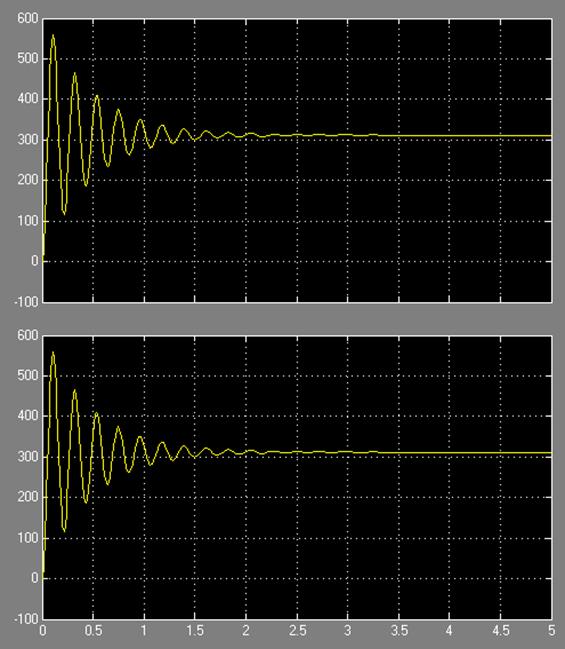
Рис. 21 – моделирование САУ по схеме и передаточной функции