Алгебра логики
Оглавление
Таблицы истинности. 2
Таблицы истинности основных операций. 2
Задачи. 3
Поразрядные операции. 4
Основные законы алгебры логики. 5
Тождества. 6
Правила поглощения и склеивания. 6
Задачи. 7
Переход от табличной формы функции алгебры логики к аналитической 9
Запись функции по единицам. 9
Запись функции по нулям. 9
Логические функции от двух аргументов. 9
Стрелка Пирса. 10
Функция следования (импликация от A к B) 11
Функция эквивалентность. 11
Штрих Шеффера. 11
Приоритет основных логических операций. 12
Задачи. 12
Минимизация функций алгебры логики с помощью карт Карно. 13
Правило записи функции по карте Карно по единицам. 14
Карта Карно для функции от 4 переменных. 15
Запись функции по нулям. 18
Правило записи функции по карте Карно по нулям. 18
В алгебре логики операции выполняются над переменными, которые могут принимать 2 значения: истина (true) или ложь (false – фальшь). Истина обычно обозначается 1, а ложь – 0.
Эти переменные соответствуют утверждениям, относительно которых можно сказать, истинны они или ложны. Такие утверждения называются высказываниями.
Кроме того, эти переменные могут соответствовать наличию или отсутствию электрических потенциалов в переключательных (электронных схемах), поэтому аппарат алгебры логики используют для описания электронных схем.
В программировании логической переменной соответствует результат проверки отношения, например: x>0.
Логические переменные обычно обозначают латинскими буквами: A, B, C, … x, y, z.
В алгебре логики определены несколько логических операций над логическими переменными, основные из них: И, ИЛИ, НЕ.
Таблицы истинности
Таблицы истинности представляют собой таблицы, в которых перечислены все возможные комбинации значений аргументов и соответствующие им значения функций.
Таблицы истинности основных операций
1. Операция НЕ (логическое отрицание или инверсия).
Отрицание обычно обозначают:  или
или  .
.
В языке С/C++ отрицание обозначают знаком!, например:!(a>0) (это соответствует отношению a <= 0).

|  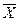
|
 Операция НЕ меняет 0 на 1, а 1 – на 0.
Операция НЕ меняет 0 на 1, а 1 – на 0.
Условное графическое изображение логической схемы, осуществляющей инверсию сигнала:
2. Операция И (логическое умножение, или конъюнкция).
Логическое умножение обычно обозначают знаком & (амперсанд) или  . Когда понятно, что речь идет о логическом умножении, используют точку или опускают знак этой операции.
. Когда понятно, что речь идет о логическом умножении, используют точку или опускают знак этой операции.
В языке С/C++ логическое умножение обозначают знаком &&, например:
(x == 0) && (y == 0).
| X | Y | X & Y |
 Операция И дает значение 1 только в одном случае, когда оба операнда равны 1.
Операция И дает значение 1 только в одном случае, когда оба операнда равны 1.
Условное графическое изображение логической схемы, осуществляющей логическое умножение сигналов:
| X | Y | X  Y Y
|
3. Операция ИЛИ (логическое сложение, или дизъюнкция).
Логическое сложение обычно обозначают знаком V. Когда понятно, что речь идет о логическом сложении, используют знак +.
В языке С/C++ логическое сложение обозначают знаком ||, например: (x == 0) || (y == 0).
 Операция ИЛИ дает значение 0 только в одном случае, когда оба операнда равны 0.
Операция ИЛИ дает значение 0 только в одном случае, когда оба операнда равны 0.
Условное графическое изображение логической схемы, осуществляющей логическое сложение сигналов:
Приоритет операций
1) Унарное НЕ (когда операция относится к одной переменной).
2) Логическое умножение &
3) Логическое сложение 
Задачи
Задача 1 Вычислить значение логического выражения
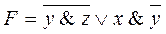 при x = 1, y = 1, z = 0
при x = 1, y = 1, z = 0
Решение:
1) y & z = 1 & 0 = 0 2)  =
=  = 1
= 1
3) 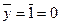
 4)
4) 
5)  Ответ: F = 1
Ответ: F = 1
Задача 2
Построить таблицу истинности функции: 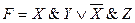
Запишем все возможные комбинации значений переменных и будем заполнять таблицу по столбцам.
Количество строк в таблице истинности = 2n, где n- количество логических аргументов функции. В данном случае n = 3, следовательно в таблице должно быть 8 строчек, не считая заголовка.
Чтобы записать все возможные комбинации значений аргументов, можно рассматривать их как двоичные числа от 000 до 111 (от 0 до 7).
Другой способ записи всех возможных комбинаций значений аргументов состоит в следующем:
| X | Y | Z | 
| X & Y | 
| F | |
1) разделить столбец значений первой переменной пополам и заполнить верхнюю часть колонки нулями, а нижнюю – единицами.
2) Разделить столбец значений второй переменной на 4 части и заполнить четверти чередующимися группами нулей и единиц, начиная с группы нулей.
3) Продолжить деление столбцов пополам и заполнение их чередующимися группами нулей и удиниц; в последнем столбце должна идти последовательность: 0 1 0 1 0 1…
Поразрядные операции
Поразрядные операции применяют к двоичным кодам в каждом разряде отдельно.
1) поразрядная операция НЕ:
в языке С/C++ обозначается знаком ~(тильда)
~00110101 à 11001010
эта операция заменяет каждый 0 на 1 и наоборот.
2) поразрядная операция ИЛИ:
в языке С/C++ обозначается знаком |
 |
эта операция обычно используется для того, чтобы установить 1 в определенном разряде числа.
3)
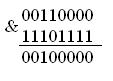 |
поразрядная операция И:
в языке С/C++ обозначается знаком &
эта операция используется для того, чтобы установить 0 в определенном разряде числа, или для того, чтобы проверить, стоит ли в определенном разряде 1.
Второй операнд операций & и | обычно называется маской.
В языке С/C++ есть еще операции сдвига, которые тоже относятся к поразрядным. Эти операции применимы только к целым числам.
4) сдвиг влево на n разрядов: X << n приводит к тому, что левые n разрядов кода величины X пропадают, а справа добавляется n нулей:
00110011 << 2 à 11001100
Каждый сдвиг влево увеличивает число в 2 раза (если слева не пропадают значащие цифры)
5) сдвиг вправо на n разрядов: X >> n приводит к тому, что правые n разрядов кода величины X пропадают, а слева добавляется n нулей:
00110011 >> 2 à 00001100
Каждый сдвиг вправо приводит к уменьшению числа в 2 раза (деление нацело).