Логическая функция - это функция, в которой переменные принимают только два значения: логическая единица или логический ноль. Истинность или ложность сложных суждений представляет собой функцию истинности или ложности простых. Эту функцию называют булевой функцией суждений f (a, b).
Любая логическая функция может быть задана с помощью таблицы истинности, в левой части которой записывается набор аргументов, а в правой части - соответствующие значения логической функции. При построении таблицы истинности необходимо учитывать порядок выполнения логических операций.
Порядок выполнения логических операций в сложном логическом выражении:
1. инверсия;
2. конъюнкция;
3. дизъюнкция;
4. импликация;
5. эквивалентность.
Для изменения указанного порядка выполнения операций используются скобки.
Для каждого составного высказывания (логического выражения) можно построить таблицу истинности, которая определяет его истинность или ложность при всех возможных комбинациях исходных значений простых высказываний (логических переменных).
При построении таблицы истинности целесообразно руководствоваться определенной последовательностью действий.
Алгоритм построения таблиц истинности для сложных выражений:
1. Определить количество строк:
количество строк = 2n + строка для заголовка,
n - количество простых высказываний.
2. Определить количество столбцов:
количество столбцов = количество переменных + количество логических операций;
o определить количество переменных (простых выражений);
o определить количество логических операций и последовательность их выполнения.
3. Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности с учетом таблиц истинности основных логических операций.
|
|
Пример: Составить таблицу истинности логического выражения:
D = А & (B C).
Решение:
1. Определить количество строк:
на входе три простых высказывания: А, В, С поэтому n=3 и количество строк = 23 +1 = 9.
2. Определить количество столбцов:
o простые выражения (переменные): А, В, С;
o промежуточные результаты (логические операции):
o А - инверсия (обозначим через E);
o B C - операция дизъюнкции (обозначим через F);
o а также искомое окончательное значение арифметического выражения:
o D = А & (B C). т.е. D = E & F - это операция конъюнкции.
3. Заполнить столбцы с учетом таблиц истинности логических операций.
| A | B | C | E | F | E & F |
Построение логической функции по ее таблице истинности:
Попробуем решить обратную задачу. Пусть дана таблица истинности для некоторой логической функции
Z(X,Y):
| X | Y | Z |
Составить логическую функцию для заданной таблицы истинности.
Правила построения логической функции по ее таблице истинности:
1. Выделить в таблице истинности те строки, в которых значение функции равно 1.
2. Выписать искомую формулу в виде дизъюнкции нескольких логических элементов. Число этих элементов равно числу выделенных строк.
|
|
3. Каждый логический элемент в этой дизъюнкции записать в виде конъюнкции аргументов функции.
4. Если значение какого-либо аргумента функции в соответствующей строке таблице равно 0, то этот аргумент взять с отрицанием.
Решение.
1. В первой и третьей строках таблицы истинности значение функции равно 1.
2. Так как строки две, получаем дизъюнкцию двух элементов: () V ().
3. Каждый логический элемент в этой дизъюнкции запишим в виде конъюнкции аргументов функции X и Y: (X & Y) V (X & Y).
4. Берем аргумент с отрицанием если его значение в соответствующей строке таблицы равно 0 и получаем искомую функцию:
5. Z (X, Y) =(X & Y) V (X & Y).
Пример 4. Определить участника преступления, исходя из двух посылок:
1) "Если Иванов не участвовал или Петров участвовал, то Сидоров участвовал";
2) 2) "Если Иванов не участвовал, то Сидоров не участвовал".
Решение
Составим выражения:
I - "Иванов участвовал в преступлении";
P - "Петров участвовал в преступлении";
S - "Сидоров участвовал в преступлении".
Запишем посылки в виде формул:
Тогда
Проверим результат, используя таблицу истинности:
Ответ: Иванов участвовал в преступлении.
Количество входных переменных в заданном выражении равно трем (A,B,C). Значит, количество входных наборов Q=23=8.
Столбцы таблицы истинности соответствуют значениям исходных выражений A,B,C, промежуточных результатов 
и (B V C), а также искомого окончательного значения сложного арифметического выражения 
:
| A | B | C |
| B V C |
|
|
|
Примеры.
1. Составим таблицу истинности для формулы 
, которая содержит две переменные x и y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах - значения промежуточных формул и в последнем столбце - значение формулы. В результате получим таблицу: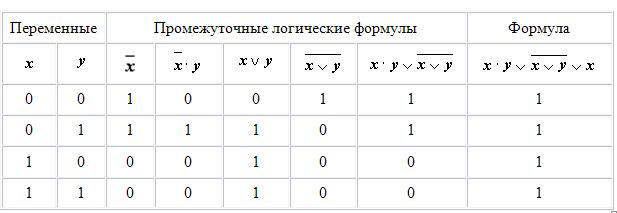 
Из таблицы видно, что при всех наборах значений переменных x и y формула 
принимает значение 1, то есть является тождественно истинной.
2. Таблица истинности для формулы 
Из таблицы видно, что при всех наборах значений переменных x и y формула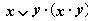 
принимает значение 0, то есть является тождественно ложной.
3. Таблица истинности для формулы 
:
Из таблицы видно, что формула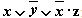 
в некоторых случаях принимает значение 1, а в некоторых - 0, то есть является выполнимой.
Пример1:
Вася спросил у мамы: «Можно пойти в кино или на футбол?» Мама ответила отрицательно. Как поступить мальчику?
Проверим правильность этого закона с помощью таблицы истинности.
Пример2:
В классе оказалось разбито стекло. Учитель объясняет директору: это сделал Коля или Саша. Но Саша этого на делал, т.к. в это время сдавал мне зачет. Следовательно, это сделал Коля
Решение: Формализуем данное сложное высказывание.
К - это сделал Коля
С - это сделал Саша
Кол-во простых высказываний n = 2.
Форма высказывания:
